数据的修约规则

一、检测数据分类及处理

1、数据分类

      试验检测的原始检测数据，按其性质可分为计量值和计数值两种。

①计量值

       计量值为连续数据，可以不断细分。一般都可以用测量工具或仪器来测量或试验，可表示大小和单位，一般都带有小数值。

②计数值

       计数值为间断、离散的数值，不可以用测量器具来测量，只能用计数的方法来数出个数或次数。一般没有单位，只有大小且只能用整数（P数据）或百分数（P_n数据）表示。

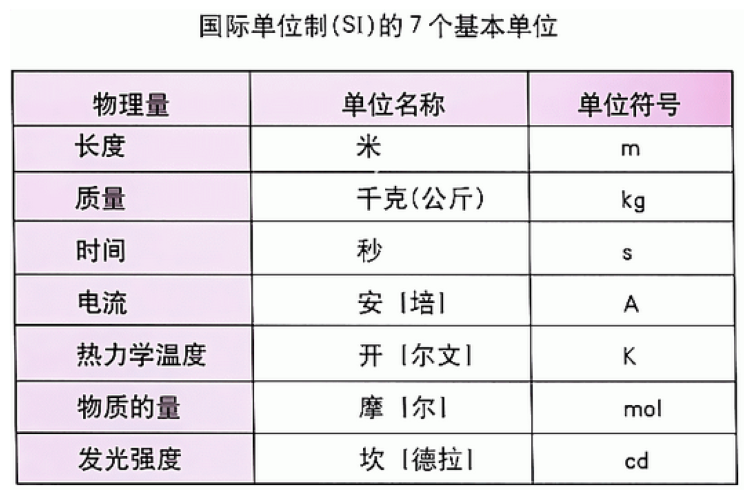
 注：1954年第十届国际计量大会决定采用米(m)、千克(kg)、秒(s)、安培(A)、开尔文(K)和坎德拉(cd)作为基本单位。1960年第十一届国际计量大会决定将以这六个单位为基本单位的实用计量单位制命名为“国际单位制”，并规定其符号为“SI”。1974年的第十四届国际计量大会又增加将物质的量的单位摩尔(mol)作为基本单位。因此，目前国际单位制共有七个基本单位。

2、数据处理

①叙述性工作

       将收集到的试验数据加以整理和归纳，用列表和作图的方法，把这些数据的主要特征点表现出来。

②分析性工作

       将整理、归纳后所得到的数字资料加以分析，找出这些数字资料所遵循的规律。

③推断性工作

       分析数据资料并发现它们所遵循的规律以后，就要根据所发现的规律，进行推测性的判断，然后根据这些推测出来的规律，去预测未来事物发生的情况。

二、数字的修约规则

1、有效数字

   指由数字组成的一个数，除最末一位数字是不确切值或可疑值外，其他数字皆为可靠值或确切值，则组成该数的所有数字包括末位数字称为有效数字，除有效数字外其余数字为多余数字。

   整数前面的 “ 0” 无意义，是多余数字。对纯小数，在小数点后，数字前的 “ 0” 也是多余数字。处于数中间位置的 “ 0” 是有效数字。

   处于数后面位置的 “ 0” 是否算有效数字可分三种情况：

（1）数后面的 “ 0”，若把多余数字的 “ 0” 用10 的乘幂来表示，使其与有效数字分开，这样在10 的乘幂前面所有数字包括 “ 0” 皆为有效数字；

（2）作为测量结果并注明误差值的数值，其表示的数值等于或大于误差值的所有数字，包括 “ 0” 皆为有效数字；

（3）除以上两种情况以外的表示方法均为不确切表示法，应避免。

2、修约间隔

  修约间隔是指确定修约保留位数的一种方式。修约间隔的数值一经确定，修约值即应为该数值的整数倍。

  例如指定修约间隔为0.1, 相当于将数值修约到一位小数。又如指定修约间隔为100,修约值即应在100的整数倍中选取,相当于将数值修约到“百”数位。

  0.5单位修约（半个单位修约）是指修约间隔为指定数位的0.5单位，即修约到指定数位的0.5单位。

  0.2单位修约是指修约间隔为指定数位的0.2单位，即修约到指定数位的0.2单位。

  最基本的修约间隔是10ⁿ（n为整数）,它等同于确定修约到某数位。

3、修约规则

（1）拟舍弃数字的最左一位数字小于5时，则舍去，保留的各位数字不变。

   例：将18.2432修约到一位小数，则为18.2，修约到两位有效数字则为18。

（2）拟舍弃数字的最左一位数字大于5；或者是5,而且后面的数字并非全部为0时,则进1,即保留的末位数字加1。

   例：将18.553修约到一位小数，则为18.6; 18.563修约为18.6。

（3）拟舍弃数字的最左一位数字为5,而后面无数字或全部为0时,若所保留的末位数字为奇数（1,3,5,7,9）则进一,若为偶数时（2,4,6,8,0）则舍弃。

   例：2.050修约间隔为0.1，则为2.0；4500修约间隔为1000，则为4×10³；5500修约间隔为1000，则为6×10³。

（4）负数修约时，先将它的绝对值按上述三条规定进行修约，然后在修约值前面加负号。

（6）0.5单位修约时，将拟修约数字乘以2，按指定的数位根据修约规则进行修约，所得数值除以2。

  例如将下列数字修约到个位数的0.5单位：

     50.25 →100.50（×2）→100（修约间隔1）→50.0

    -50.38 →-100.76（×2）→-101（修约间隔1）→-50.5

（7）0.2单位修约时，将拟修约数字乘以5，按指定的数位根据修约规则进行修约，所得数值除以5。

  例如将下列数字修约到百位数的0.2单位：

830 →4150（×5）→4200（修约间隔100）→840（修约间隔为20）

842 →4210（×5）→4200（修约间隔100）→840（修约间隔为20）

（8）拟舍去数字并单独非一个数字时，不得对数值连续修约，应按拟舍去数字的最左面的第一位数字大小，按修约规则一次修约到位。

例如：修约15.4546 ，修约间隔为1 ，

 正确：15.454 →15；不正确：15.4546→15.455→15.46→15.5→16。

  修约规则总结成以下口诀：四舍六入五考虑，五后非零则进一，五后为零视奇偶，奇升偶舍要注意，修约一次要到位。

4、计算法则

①加减运算

  应以各数中有效数字末位数的数位最高者为准 （小数即以小数部分位数最少者为准），其余数均比该数向右多保留一位有效数字。多保留一位小数第的目的，是为了不因凑整而严重影响结果的精度，多保留的一位数常称为安全数字。

例：计算41.3+3.012+0.322+0.0578，经分析应为 

        41.3+3.01+0.32+0.06=44.69

    那么0.57+0.4+0.3345+0.378=？

②乘除运算

  应以各数中有效数字位数最少者为准，其余数均多取一位有效数字，所得积或商也多取一位有效数字。

例：计算0.0122 ×26.52 ×1.06892 ,经分析应为

      0.0122 ×26.52 ×1.069 ＝0.3459

③平方或开方运算

  结果可比原数多保留一位有效数字。

④对数运算

  所取对数位数应与真数有效数字位数相等。

习题

修约以下数字

15.3528（保留两位小数）；

125.555（保留整数）；

15.3528（保留一位小数）；

19.998（保留两位小数）；

10.0500001（保留一位小数）；

16.6875（保留三位小数）；

10.35（保留一位小数。