课时2 插补原理
一、几个名词:
I.为什么要进行插补?
因为数控机床的进给运动都是沿坐标轴平行移动,而刀具相对工件移动的轨迹是空间的曲线,为此要把空间曲线插补后转变为各个坐标轴的直线运动,合成后成为空间的曲线运动。
II.插补定义?
在已知线段类型起点、终点和圆心坐标等情况下,计算各个坐标轴位移量后,补足中间点坐标的过程。
III.插补的分类:脉冲增量法(逐点比较法、数字积分法)和数据采样法。
二. 逐点比较法插补
逐点比较法插补的基本原理是,逐点比较刀具与编程轮廓之间的相对位置,并根据比较结果决定下一步的进给方向,使刀具向减小偏差的方向进给,而且每次只有一个方向的进给,周而复始,直至全部结束,从而获得一个非常接近于编程轮廓的轨迹。
第一拍:偏差判别—偏差当前位置相对于编程轮廓的偏离情况,以决定进给方向。
第二拍:进给—根据偏差判别结果,控制相应的坐标轴进给一步,使刀具向编程轮廓靠拢,减小偏差。然后计算当前点的动点坐标。
第三拍:新偏差计算—刀具进给一步后,计算新的偏差,作为下一次偏差判别的依据。
第四拍:终点判别—每进给一步,都要判别刀具是否到达终点,若已到达终点,则停止插补,否则,继续循环以上4个节拍,直至到达终点。
1). 逐点比较法直线插补
(1). 插补原理
如图3.21所示,以第I象限直线/OE,起点O为坐标原点,终点E(Xe,Ye),动点坐标为Ni(Xi,Yi)。
第一拍:偏差判别,动点坐标可能在/OE上、上方、下方。
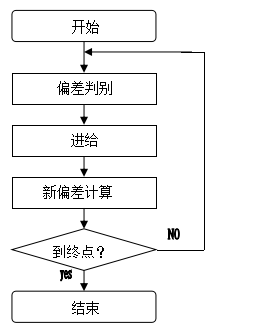
图3.20逐点比较法插补流程
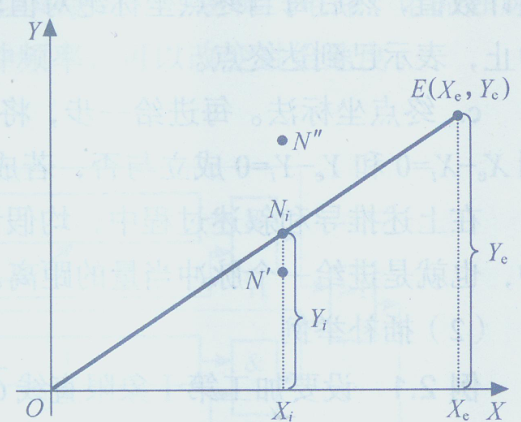
图3.21 动点与直线之间的关系图
则:![]() 正好在/OE上。
正好在/OE上。
![]() 在/OE上方。
在/OE上方。
![]() 在/OE的下方
在/OE的下方
![]() 叫第i次插补后的偏差函数。其符号反映了动点Ni和直线/O的相对位置。
叫第i次插补后的偏差函数。其符号反映了动点Ni和直线/O的相对位置。
第二拍:进给方向由偏差判别的结果来决定。对第I象限直线插补来说
Fi≥0,向+X方向进给一步, Fi∠0,向+Y方向进给一步。
第三拍:新偏差计算
刀具在编程的起O,则偏差F0=0。i次插补后,刀具运动在Ni点,偏差![]() 。
。
Fi≥0,Xi+1=Xi+1;Yi+1=Yi ![]() 偏差递推公式。
偏差递推公式。
Fi∠0,Xi+1=Xi;Yi+1=Yi+1 ![]() 偏差递推公式。
偏差递推公式。
可见,新偏差函数的Fi+1 计算,仅与终点坐标(Xe,Ye)和上一点的偏差函数Fi有关,不做乘法,只做加减运算,从而提高了插补运算速度。
第四拍—终点判别。刀具每进给一次都要进行一次终点判别。常用终点判别方法有:
a. 总步长法,计算总步长![]() ,每进给一步,总步长减1,直到总步长为0,表示到达终点。
,每进给一步,总步长减1,直到总步长为0,表示到达终点。
b.投影法,以终点坐标绝度值较大者作为总步长,若对应的坐标轴进给一步,终点值减1,判别如总步长为0 ,表示到达了终点。
c.终点坐标法,每进给一步,都将动点坐标与终点坐标比较,如果
![]()
![]() 表示已到终点,停止插补,否则继续插补。
表示已到终点,停止插补,否则继续插补。
(2)直线插补举例
例题4.1 设要加工第I象限直线/OE,起点在原点O,终点在E(3,5)试用逐点比较法进行直线插补。
解:总部长![]() ,开始刀具起点在O点,在直线上,所以初始偏差F0=0,直线插补的运算过程如表4.5所示,插补的过程轨迹如图3.22所示。需要注意的是,对于逐点比较法插补,起点和终点处刀具均落在编程轮廓上,也就是说在编程开始和结束时,偏差函数均为零,及F=0,否则说明插补过程中出现了错误。
,开始刀具起点在O点,在直线上,所以初始偏差F0=0,直线插补的运算过程如表4.5所示,插补的过程轨迹如图3.22所示。需要注意的是,对于逐点比较法插补,起点和终点处刀具均落在编程轮廓上,也就是说在编程开始和结束时,偏差函数均为零,及F=0,否则说明插补过程中出现了错误。
表4.2 逐点比较法直线插补运算过程表
序号 | 偏差判别 | 进给 | 偏差计算 | 终点判别 |
起点0 | F0=0 |
| ||
1 | F0=0≥0 | +ΔX | F1=F0-Ye=0-5=-5 |
|
2 | ||||
3 | ||||
4 | ||||
5 | ||||
6 | ||||
7 | ||||
8 | F7=-3∠0 | +ΔY | F8=F7+Xe=-3+3=0 |
|

图3.22 逐点比较法直线插补应用举例
(3)插补的实现
逐点比较法插补实现的方法,既可以采用硬件逻辑、也可以利用软件编程来实现。硬件逻辑实现速度快、减轻了CPU的负担,进来FPG等可编程逻辑阵列构成插补器,可靠性进一步提高,得到了广发的应用。软件插补灵活性高,但运行速度较慢,但随着计算机技术的不断发展,CPU处理速度大大提高,专用CPU实现插补也得到广泛应用。
例4.2 用MCS-51单片机实现起点O(0,0)终点在E(30mm,40mm),假设脉冲当量δ为1mm,计算机字长为8位。
ORG 0000H | |||
1 | MAIN: | MOV TMOD,#01H ; | 定时器0设置为定时方式1 |
2 | MOV 30H,#30 ; | X终点坐标Xe=30mm送给30H。 | |
3 | MOV 31H.#40 ; | Y终点坐标Ye=40mm送给31H。 | |
4 | MOV 40H,0 ; | 40H为偏差单元,首偏差F0=0 | |
5 | MOV P1,#0 ; | 关闭步进电机的输出 | |
6 | MOV A,30H ; | ||
7 | ADD A,31H ; | ||
8 | MOV 50H,A ; | 计算总步数在50H单元。 | |
9 | MOV A,31H ; | ||
10 | CPL A ; | ||
11 | ADD A,#01 ; | ||
12 | MOV 31H,A ; | 求【-Ye】补→31H | |
13 | LOOP: | MOV TH0,#0FDH ; | 置定时器的系数 |
14 | MOV TL0,#12H ; | 确定插补速度 | |
15 | SETB TR0 ; | 起动定时器 | |
16 | MOV A,40H ; | 取出偏差函数F | |
17 | JB ACC.7 ,STEP_Y ; | F∠0,转Y轴进给处理程序 | |
18 | ACALL PX ; | F≥0,调X轴进给分支程序,进给+ΔX | |
19 | MOV A,40H ; | 取出偏差函数F | |
20 | ADD,31H ; | F+【-Ye】补 | |
21 | MOV 40H,A ; | →F | |
22 | JNB TF0,$ ; | 等待定时时间到 | |
23 | CLR TF0 ; | 关定时标志位 | |
24 | DJNZ 50H,LOOP ; | 总步数-1如果不等于零返回继续 | |
25 | AJMP PEND ; | 若等于零,转插补结束程序 | |
26 | STEP_Y: | ACALL PY ; | 调Y轴进给分支程序,进给+ΔY |
27 | MOV A,40H ; | 计算新偏差取出偏差 | |
28 | ADD A,30H ; | F+Xe→F | |
29 | MOV 40H,A ; | ||
30 | JNB TF0 ; | 等待定时时间到 | |
CLR TF0 ; | 关定时标志位 | ||
31 | DJNZ 50H,LOOP | 总步数-1如果不等于零返回继续 | |
32 | PEND: | AJMP $ | 如果等于零,停止插补转移到其他程序 |
33 | PX: | … | X轴进给环形分配子程序 |
34 | … | ||
35 | RET | 子程序返回 | |
36 | PY: | … ; | X轴进给环形分配子程序 |
37 | … ; | ||
38 | RET ; | 子程序返回 | |
39 | END ; | 汇编结束 | |
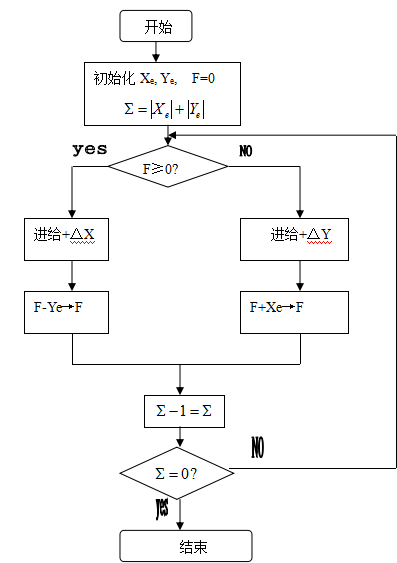
图3.23 逐点比较法直线插补流程图
2.逐点比较法圆弧插补
(1)插补原理
在圆弧加工过程中,要描述刀具与编程圆弧之间的选相对位置,可用动点到圆心的距离大小来反映,如图4.24所示,假设编程轮廓为第I象限逆园弧SE,圆心为O(0,0),半径为R,刀具动点坐标为Ni(Xi , Yi)

图3.24 第I象限逆园弧与动点之间的关系
第一步:偏差函数 ![]()
如果Ni正好落在圆弧SE上时, 则:![]()
如果Ni正好落在圆弧SE外侧时,则:![]()
如果Ni正好落在圆弧SE内侧时,则:![]()
第二步:进给方向
F≥0时,向-X方向进给一步(-ΔX);
F∠0时,向+Y方向进给一步(+ΔY);
第三步:新偏差的计算
开始时,刀具位于圆弧的起点S,因此F=0;
经过i次插补后,当前刀具在 Ni(Xi , Yi)点,对应的偏差函数为![]()
若F≥0时,向-X方向进给一步(-ΔX),动点坐标Ni+1(Xi -1, Yi)点,从而新偏差为:
![]()
若F∠0时,向+Y方向进给一步(+ΔY),动点坐标Ni+1(Xi , Yi+1)点,从而新偏差为:
![]()
可见逐点比较法圆弧插补的偏差函数递推公式中,处了加减运算外,还有乘2运算,并且与动点坐标Ni(Xi , Yi)也有关。
第四步:终点判别,和直线插补一样,插补过程中,也要进行终点判别,对于仅在一个象限的圆弧,仍然可以采用同直线一样的终点判别法;
a. 总步长法,![]()
b.投影法,![]()
c.终点坐标法,每进给一步,都将动点坐标与终点坐标比较,如果
![]()
![]() 表示已到终点,停止插补,否则继续插补。
表示已到终点,停止插补,否则继续插补。
第一象限逐点比较法圆弧插补的流程图如图4.24所示
(2)逐点比较法圆弧插补应用举例
例4.2 要加工第I象限的逆圆弧SE,起点在S (4,3),终点在E(0,5)用逐点比较法进行圆弧插补。
解:总步数![]() 开始刀具处于起点S(4,3)处,所以F=0,插补运算过程如表4.4 插补轨迹如图4.25所示。
开始刀具处于起点S(4,3)处,所以F=0,插补运算过程如表4.4 插补轨迹如图4.25所示。
![]()

图3.24 第I象限逆园弧逐点比较法插补流程图
表3.3 逐点比较法圆弧插补运算过程表
序号 | 偏差判别 | 进给 | 偏差计算与动点坐标修正 | 终点判别 | |
起点 | F0=0 | X0=4 ,Y0=3 |
| ||
1 | F0=0≥0 | -ΔX | F1=F0-2X0+1 =0-2×4+1=-7 | X1=4-1=3 Y1=3 |
|
2 | F1=-7∠0 | +ΔY | F2=F1+2Y1+1 =-7+2×3+1=0 | X2=3 Y2=3+1=4 |
|
3 | F2=0≥0 | -ΔX | F3=F2-2X2+1 =0-2×3+1=-5 | X3=3-1=2 Y3=4 |
|
4 | F3=-5∠0 | +ΔY | F4=F3+2Y3+1 =-5+2×4+1=4 | X4=2 Y4=4+1=5 |
|
5 | F4=4≥0 | -ΔX | F5=F4-2X4+1 =4-2×2+1=1 | X5=2-1=1 Y5=5 |
|
6 | F5=1≥0 | -ΔX | F6=F5-2X5+1 =1-2×1+1=0 | X6=1-1=0 Y5=5 |
|

图3.25逐点比较法第I象限逆园圆弧插补轨迹图
3.插补象限和圆弧插补走向处理
以上介绍的直线插补和圆弧插补,均是针对第I象限直线和逆园弧这种特殊情况进行的。但实际上,任何机床都必须具备处理不同象限,不同走向轮廓曲线的能力,而这时其插补计算公式和脉冲进给方向都是不同的,一般可作如下处理。
现将第I、II、III、IV象限内的直线分别记为L1、L2、L3、L4;针对起点不在原点的直线,可采用坐标平移的方法使其起点在原点。仿照第I象限直线插补的情况,不难推出4个象限直线插补的进给方向如图3.26所示。
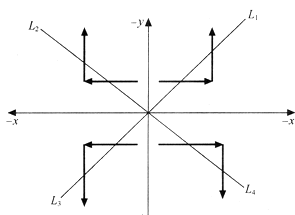
图3.26 四象限直线插补
(2)四象限圆弧插补
对于圆弧“S”表示顺园,用“N”表示逆园,结合象限的区别,可获得8种圆弧的形式,4个象限顺圆弧可以表示为SR1、SR2、SR3、SR4;4个象限逆圆弧可以表示为NR1、NR2、NR3、NR4,对于圆心不在原点的圆弧,同样可以采用坐标平移的方法使圆心在原点,仿照第I象限逆圆弧插补的情况,不难推出4个象限圆弧插补的进给方向如图3.27所示
此外,对于跨越几个象限的圆弧插补,还要考虑过象限问题,此时,可以根据圆弧过象限时必有一个坐标值为零,以及圆弧过象限时的走向不变(逆圆弧过象限的顺序是:NR1→NR2→NR3→NR4→NR1…顺圆弧过象限的顺序是:SR1→SR2→SR3→SR4→SR1…)的原则,调用不同的插补算法。在终点判别方法上,需要采用终点坐标法,判别Xe-Xi=0和Ye-Yi=0成立与否,若成立,则停止插补,否则继续。
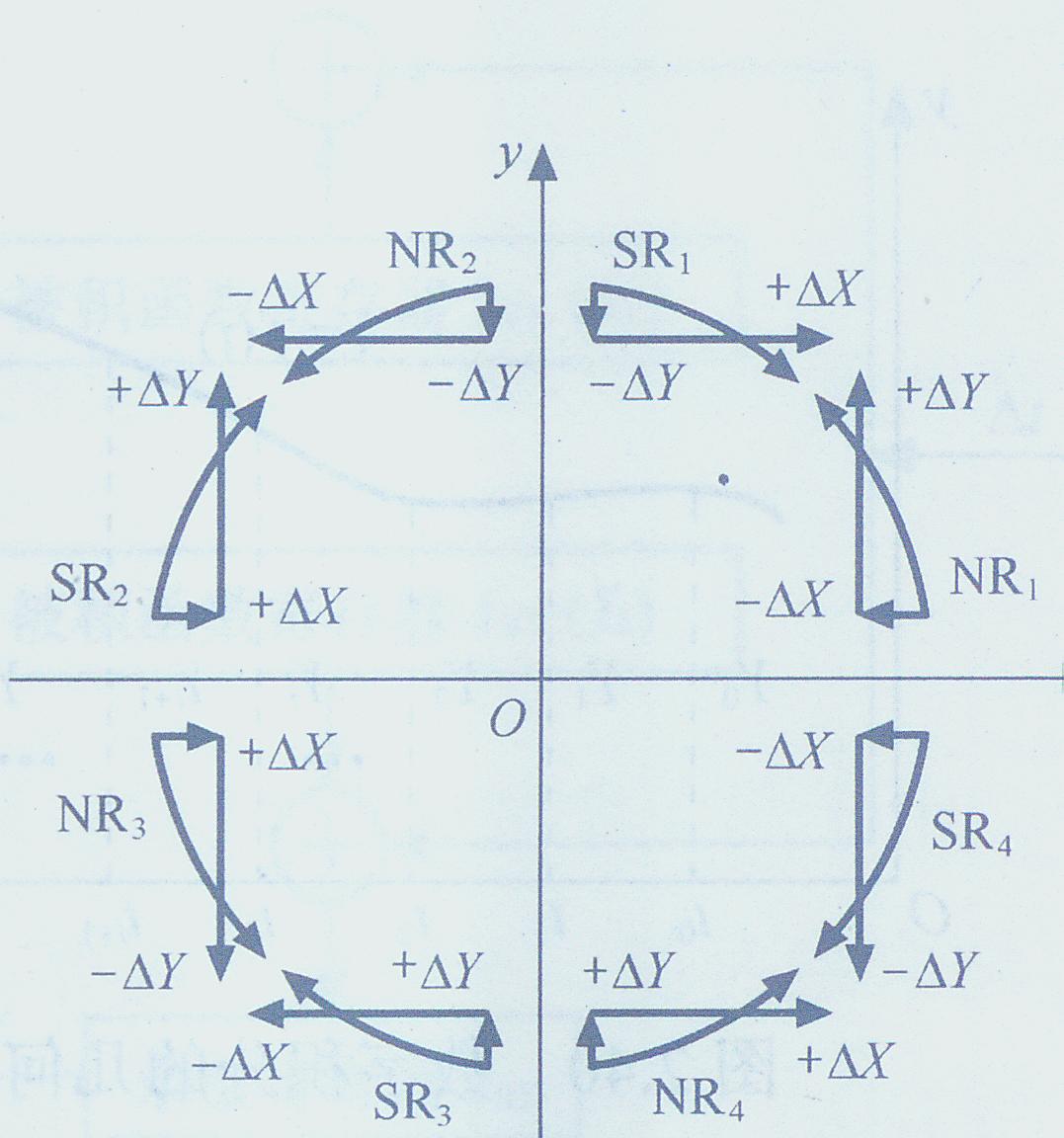
图3.28 圆弧过象限的8种不同情况
二.数字积分法直线圆弧插补
2. DD法直线插补
(1)插补原理
图3.29所示,第I象限直线/OE,起点为坐标原点,终点为E(Xe,Ye)刀具进给速度在两个坐标上的分量为。从而可求得刀具在X,Y方向上的位移增量分别为:
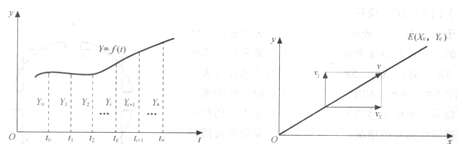
a) 数字积分的几何描述 b)DDA直线插补
图3.29 DDA插补描述和直线插补
![]()
![]()
所以: ![]()
经过m次插补后,到达(Xm,Ym)
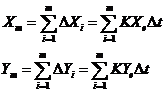
Δt=“1”单位,则
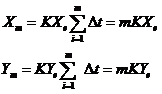
若经过n次插补,到达终点E(Xe,Ye)则,
![]()
从而: ![]()
为了保证坐标轴上每次分配的进给脉冲不超过1个脉冲单位,则
![]()
若系统字长为N为,则Xe,Ye的最大数为![]() ,将其带入上式可得
,将其带入上式可得
![]()
![]()
也就是说进过![]() 次累加,刀具正好到达终点E。
次累加,刀具正好到达终点E。
据此给出如图3.30所示DDA直线插补器,图中被积函数寄存器Jvx和Jvy分别存放终点坐标Xe和Ye,JRX和JRY分别为对应的余数寄存器。每当脉冲源发出一个控制脉冲信号Δt ,则X积分器和Y 积分器各累加一次,当累加结果超出余数寄存器容量(![]() )时,就溢出一个脉冲ΔX 或ΔY ,这样经过
)时,就溢出一个脉冲ΔX 或ΔY ,这样经过![]() 次累加后,每个坐标轴的输出脉冲总数就等于该坐标的被积函数值Xe和Ye,从而控制刀具到达终点E。
次累加后,每个坐标轴的输出脉冲总数就等于该坐标的被积函数值Xe和Ye,从而控制刀具到达终点E。
规格化和四舍五入:当直线的终点坐标Xe和Ye除以![]() 后不是纯小数时(小数点后面第一位数为1),可以对(
后不是纯小数时(小数点后面第一位数为1),可以对(![]() )同时进行小数点右移(乘
)同时进行小数点右移(乘![]() ),直至有一个为纯小数为止,这就是小数的规格化。这样经过
),直至有一个为纯小数为止,这就是小数的规格化。这样经过![]() 次累加后,最后余数寄存器 JRX和JRY虽然没有溢出,但数据大于0.5后,可以当溢出对待,称为四舍五入法。
次累加后,最后余数寄存器 JRX和JRY虽然没有溢出,但数据大于0.5后,可以当溢出对待,称为四舍五入法。
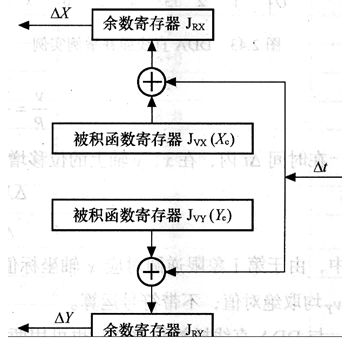
图3.30DDA直线插补流程
(2)插补举例
例2.3 设要插补第I象限直线/OE,如图3.31所示,起点在原点,终点在E(4,6),设寄存器位数为3位,试用DDA法进行插补。
解:寄存器位数为N=3,则累加次数为![]() ,插补前
,插补前
![]()
其插补过程如表2.10所示。插补轨迹如图3.31所示。
表2.10 DDA直线插补运算过程
累加次数 n | X积分器JVX=4 | Y积分器JVY=6 | 终点判别 | ||
JRX+JVX | +ΔX | JRY+JVY | +ΔY | ||
起点 | 0 | 0 | 0 | 0 | 8 |
1 | 0+4=4 | 0不进给 | 0+6=6 | 0不进给 | 7 |
2 | 4+4=8+0 | 1进给 | 6+6=8+4 | 1进给 | 6 |
3 | 0+4=4 | 0 | 4+6=8+2 | 1 | 5 |
4 | 4+4+8+0 | 1 | 2+8=8+0 | 1 | 4 |
5 | 0+4=4 | 0 | 0+6=6 | 0 | 3 |
6 | 4+4=8+0 | 1 | 6+6=8+4 | 1 | 2 |
7 | 0+4=4 | 0 | 4+6=8+2 | 1 | 1 |
8 | 4+4=8+0 | 1 | 2+6=8+0 | 1 | 0 |
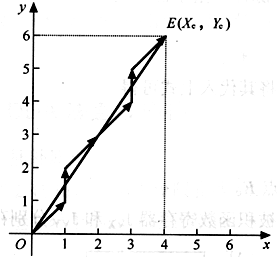
图3.31 DDA直线插补举例实例
3.DDA法圆弧插补
(1)插补原理
以第I象限逆园NR1为例,如图2.44所示,圆心在坐标原点,起点为S(XS,YS)终点为E(Xe,Ye)圆弧半径为R,进给速度为V,在两坐标轴上的进给分量为VX,VY,动点为N(Xi,Yi)则根据图中的几何关系,有如下关系式:
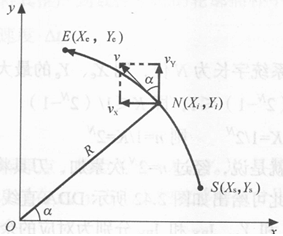
图3.32 DDA圆弧插补(NR1)
![]()
在Δt内,在X和Y轴上的位移增量分别为
![]()
与DDA直线插补相类似,也可以用两个积分器来实现圆弧插补,如图3.33所示,但必须注意它与直线插补器比较有很大的区别。
被积函数JVX,JVY的内容不同。圆弧插补时JVX对应的是Y的动点坐标,JVY对应的是X的动点坐标,所以随着圆弧插补时要随时修改JVX,JVY对应的动点坐标。

图3.33 第I象逆园插补器
对应图3.33所示NR1的DDA插补来说,插补开始时JVX,JVY分别存放起点坐标XS,YS在插补过程中,每当Y轴溢出一个脉冲(ΔY),JVX应该(+1);反之每当X轴溢出一个脉冲(ΔX),JVY应该(-1),至于何时(±1),取决于动点N所在象限和圆弧走向,图中的+和-就表示动点坐标的“+1”修正或“-1”修正的关系。
DDA圆弧插补终点判别须对X、Y两个坐标同时进行。这是可以利用两个终点计数器来实现,当X或Y坐标每输出一个脉冲,则相应终点计数器减1,当减到0时,则说明该坐标已经到达终点,并停止该坐标的累加运算,只有当两个终点计数器均减到0时,才结束整改圆弧插补过程。
(2)、插补举例
例2.4设有第I象限逆圆弧SE,起点在S(4,0)终点在E(0,4),且寄存器位数N=3。试用DDA法对此进行插补。
解:插补开始时,被积函数初值分别为
![]() ,寄存器位数为N=3。
,寄存器位数为N=3。
终点判别寄存器![]() 。其插补过程如表2.11所示,插补轨迹如图3.34中折线所示。
。其插补过程如表2.11所示,插补轨迹如图3.34中折线所示。
表2.11 DDA圆弧插补运算过程表
累加次数n | X积分器 | Y积分器 | ||||||
JVX(Yi) | JRX | ΔX |
| JVY(Xi) | JRY | ΔY |
| |
起点 | 0 | 0 | 0 | 4 | 4 | 0 | 0 | 4 |
1 | 0 | 0+0=0 | 0 | 4 | 4 | 4+0=4 | 0 | 4 |
2 | 0 | 0+0=0 | 0 | 4 | 4 | 4+4=8+0 | 1 | 3 |
3 | 1 | 0+1=1 | 0 | 4 | 4 | 0+4=4 | 0 | 3 |
4 | 1 | 1+1=2 | 0 | 4 | 4 | 4+4=8+0 | 1 | 2 |
5 | 2 | 2+2=4 | 0 | 4 | 4 | 4+0=4 | 0 | 2 |
6 | 2 | 2+4=6 | 0 | 4 | 4 | 4+4=8+0 | 1 | 1 |
7 | 3 | 3+6=8+1 | -1 | 3 | 4 | 4+0=4 | 0 | 1 |
8 | 3 | 3+1=4 | 0 | 3 | 3 | 3+4=7 | 0 | 1 |
9 | 3 | 3+4=7 | 0 | 3 | 3 | 3+7=8+2 | 1 | 0 |
10 | 4 | 4+7=8+3 | -1 | 2 | 3 | 停止 | ||
11 | 4 | 4+3=7 | 0 | 2 | 2 | |||
12 | 4 | 4+7=8+3 | -1 | 1 | 2 | |||
13 | 4 | 4+3=7 | 0 | 1 | 1 | |||
14 | 4 | 4+7=8+3 | -1 | 0 | 1 | |||
15 | 4 | 停止 | 0 | 0 | 0 | |||

图3.34 DDA圆弧插补举例 (NR1)
三. 数据采样插补
1. 基本概念
(1) 数据采样插补法
又叫时间分割法,它是以系统的位置采样周期的整数倍为插补时间间隔,根据编程进给速度将零件轮廓曲线分割成一系列微小的直线段ΔL。然后计算出每次插补与微小直线段ΔL对应的各坐标位置增量ΔX, ΔY,…,并分别输出到各坐标轴的伺服系统中,用以控制各坐标轴的进给,完成整个轮廓段的插补。
显然,数据采样法插补的每次输出结果不再是单个脉冲,而是一个数字量。所以这类插补法适用于以直流或交流伺服电动机为执行元件的闭环或半闭环数控系统中。
(2)插补周期TS与位置控制周期TC
插补周期TS—相邻两个微小直线段之间的插补时间间隔(包括插补时间和完成其他相关CNC任务的时间)一般在10ms左右;
位置控制周期TC—是两次位置采样之间的时间间隔TC一般在4~20ms左右。
TS与TC的关系—对于给定的某个数控系统其TS与TC是两个固定不变的时间参数。通常
TS≥TC,一般取TS是TC的整数倍。
(3)步长ΔL的计算
现假设编程的进给速度为F,系统的插补周期为TS,则可求得每次插补分割的微小直线段ΔL的长度为:ΔL=FTS/(60×1000)
(4)插补精度
直线插补时,插补所形成的每段小直线与编程直线重合,不会造成轮廓误差。
圆弧插补时,一般是用弦线来逼近圆弧,这些微小的直线段不可能完全与圆弧相互重合,从而会造成轮廓误差。通过分析,可以导出其最大径向误差为
![]()
式中,F为编程的进给速度。TS为插补周期,R为圆弧半径。
2. 数据采样法直线插补
(1)、基本原理
如图3.35所示,在XOY平面内的直线/OE,起点为O(0,0),终点为E(Xe,Ye),动点为N i-1(Xi-1,Yi-1),编程进给速度为F,插补周期为TS,根据数据采样法插补的有关定义,每个插补周期的进给步长为ΔL=FTS,根据几何关系,可求得插补周期内的刀具在各坐标轴方向上的位移增量分别为
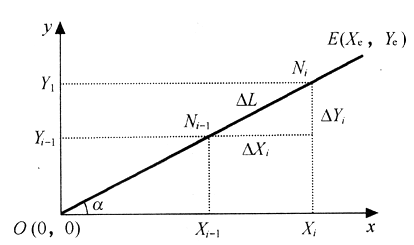
图3.35 数据采样法直线插补
![]()
式中,L为直线的长度,![]() K为系数,K=ΔL/L=FTS/L
K为系数,K=ΔL/L=FTS/L
则新的动点坐标为:
![]()
(2) 插补流程
通过前面分析可以看出,利用数据采样法来插补直线时,算法比较简单,一般可分为以下3个步骤。
一是插补准备—完成一些常量的计算工作,求出:ΔL=FTS,![]() 等的值,一般对每一个轮廓段仅执行一次。
等的值,一般对每一个轮廓段仅执行一次。
二是插补计算—每个插补周期均执行一次,求出该周期对应的坐标增量值(ΔXi, ΔYi)以及新的动点坐标值(Xi,Yi)
三是终点判别—通常根据插补余量(余量=![]() 的大小来判别是否到达终点,判别原则如下:
的大小来判别是否到达终点,判别原则如下:
若余量小于步长,则![]() ,则及将到达终点,将剩余余量
,则及将到达终点,将剩余余量
![]() 输出后插补结束。
输出后插补结束。
软件插补的流程图如图3.36所示。
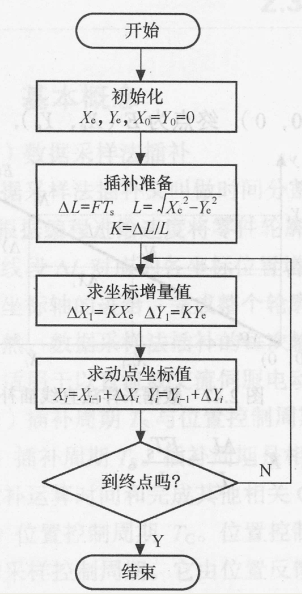
图3.36 数据采样法直线插补流程图。
3.数据采样插补法圆弧插补
(1)基本原理
数据采样法圆弧插补的基本思想是在满足加工精度的前提下,用弦线或割线来代替圆弧线实现进给,即采用直线逼近圆弧。下面以内接弦线(以弦代替圆弧)法为例,介绍其插补算法。
图3.37所示为第I象限顺圆弧,圆心在坐标原点O,起点为S(Xs,Ys)终点为E(Xe,Ye),圆弧半径为R,进给速度为F,A(Xi-1,Yi-1),B(Xi,Yi)是圆弧上两个相邻的插补点,弦/AB是圆弧AB对应的弦长![]() ,进给速度为F,插补周期为
,进给速度为F,插补周期为![]() ,则由
,则由![]() 。当刀具由A点进给到B点时,对应各坐标的增量为
。当刀具由A点进给到B点时,对应各坐标的增量为![]() 为弦/AB的终点,弦/AB所对应的圆心角为
为弦/AB的终点,弦/AB所对应的圆心角为![]() 。
。
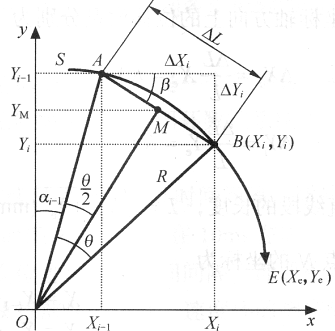
图3.37 弦线法第I象限顺圆弧插补
由于图中![]() ,所以先求
,所以先求![]() 。根据几何关系可得
。根据几何关系可得![]()
而![]() ;
;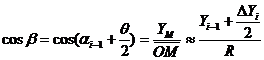
所以取![]()
又由于B点在圆弧上,所以 ![]() ,即
,即![]() 所以
所以![]()
起点处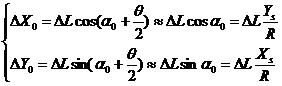
当 ![]() 时,先求出
时,先求出![]() ,后求
,后求![]() ,可得
,可得
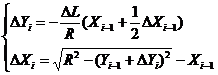
(2)插补流程
与直线插补时相似,数据采样法圆弧插补流程也分为3个步骤。
一是插补准备—计算![]()
二是插补计算—
当![]() 时,
时,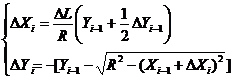
当![]() 时,
时,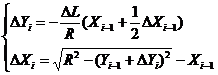
并计算新的动点坐标
![]()
三是终点判别—如果![]() ,则即将到达终点,将剩余增量
,则即将到达终点,将剩余增量![]() 输出后插补结束。
输出后插补结束。
插补的流程图如图3.38
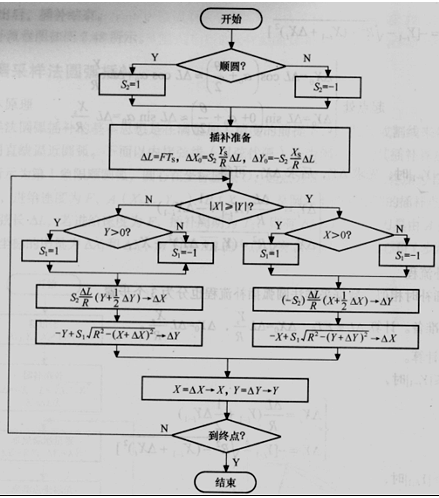
图3.38 数据采样圆弧插补法流程图
4.数据采样法插补举例
例2.5 设某闭环数控系统的插补周期为![]() ,编程进给速度
,编程进给速度 ![]() ,编程直线
,编程直线![]() 起点为O,终点坐标E(3mm,4mm)。试计算每个插补周期的各个坐标位移增量
起点为O,终点坐标E(3mm,4mm)。试计算每个插补周期的各个坐标位移增量![]() 。
。
解:根据数据采样法进给步长公式,可得每个插补周期内的步长为
![]()
编程直线段的长度L和系数K为
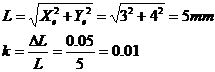
因此可求得每个插补周期的各坐标轴位移增量为
![]()


