最优控制概论

 最优控制理论是现代控制理论的主要组成部分。

 对于多输入-多输出系统，或者对控制性能要求较高的复杂控制系统，经典控制方法常常显得无能为力。

 20世纪50年代后，由于空间技术的迅速发展和计算机的广泛应用，动态系统的优化理论得到了迅速的发展，逐渐形成了最优控制这一重要的学科分支，并在工程、经济、管理、航空、航天及人口控制等方面，取得了显著的成效。

一．最优控制的基本概念

  最优控制研究的主要问题：

 根据已建立的受控对象的数学模型，选择合适的控制规律，使得受控对象能使给定的某一性能指标达到极小值（或极大值）。

 从数学分析上来说，问题实质就是求解一类带有约束条件的泛函（即函数的函数）求极值的问题，属于变分学的范畴。

 经典的变分理论只能解决控制量无约束，即容许控制量属于开集的一类最优控制问题。

为了满足工程实践的需要，20世纪50年代中期，出现了现代变分理论，其中著名的方法有动态规划和极小值（极大值）原理等。 

二．最优控制系统

各种不同类型的最优控制系统:

（1）使整个控制过程中被控量的误差达到最小的系统。例如控制系统的任务是平衡状态恒定，这就是最优镇定系统。假如控制系统的任务是以最小误差跟踪运动目标或所希望的参考轨迹（如人造卫星围绕地球的轨迹），这就是最优随动系统。

（2）使控制过程能最快地从任何初始状态转移到规定的平衡状态（即终端状态，为终端时间），这就是时间最优控制系统。 

（3）在一定条件下，能以最少能量完成控制任务的系统（例如火箭发射使卫星进入轨道的能耗为最小），这就是能量最优控制系统。

（4）在规定的终端时间（例如 t = tf ），具有最精确的终端状态 x =(tf),（例如导弹打击目标），这就是最优终端控制系统。

（5）在安全可靠的条件下，电力系统的最佳负荷分配系统；在费用最省的条件下，交通运输的最佳调度系统；最优运输线路系统等。

三．性能指标（又称目标函数）

 最优控制的性能与取什么样的性能指标有着密切的关系。所以设计最优控制系统时，要根据受控对象及生产过程的具体情况和要求，正确选择性能指标。选择性能指标时，既要考虑到能对系统的性能做出正确的评价，又要考虑到工程上能够易于实现。

性能指标的形式一般可以分成以下三种类型。

1．积分型性能指标

2．终值型性能指标

3．综合型性能指标

四．最优控制的求解方法

 最优控制问题的求解方法很多，较常用的方法有：变分法、极小值（极大值）原理、动态规划法、线性二次型最优控制法，自适应控制法、搜索法和梯度法等等。下面具体介绍较常用的基于二次型最优控制法的最优状态调节器。

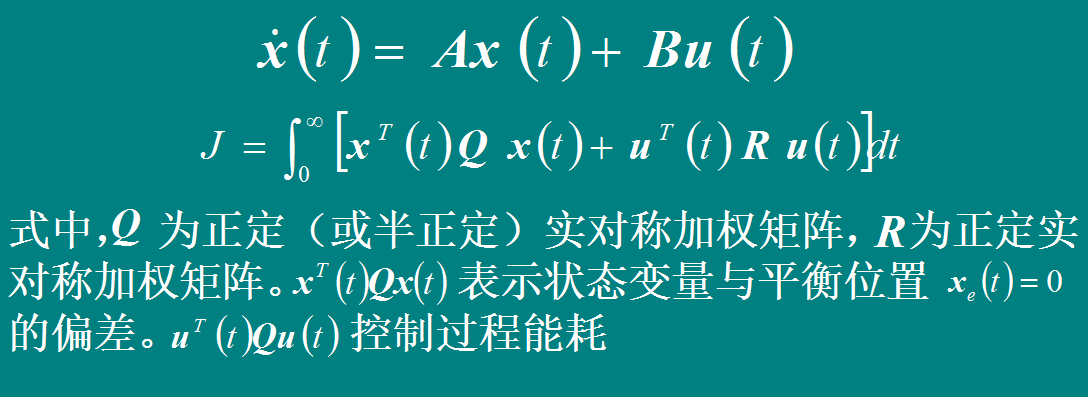
系统的结构图如图所示: