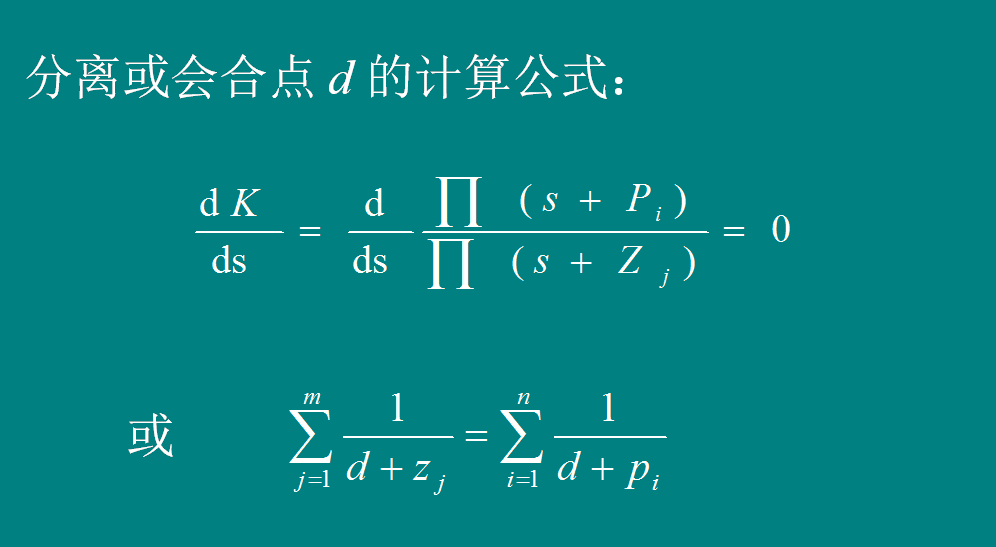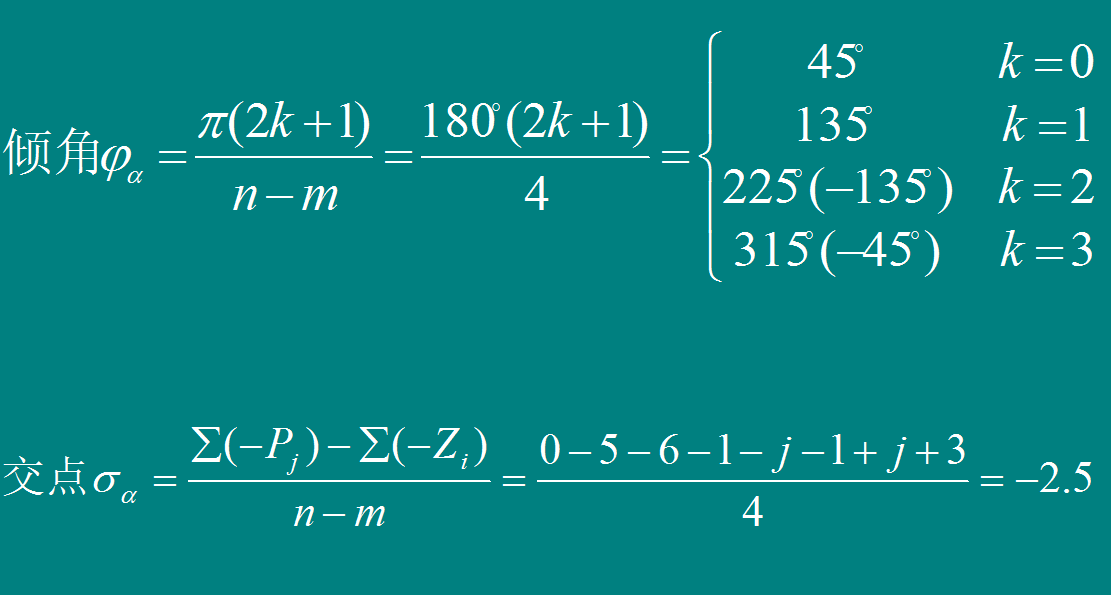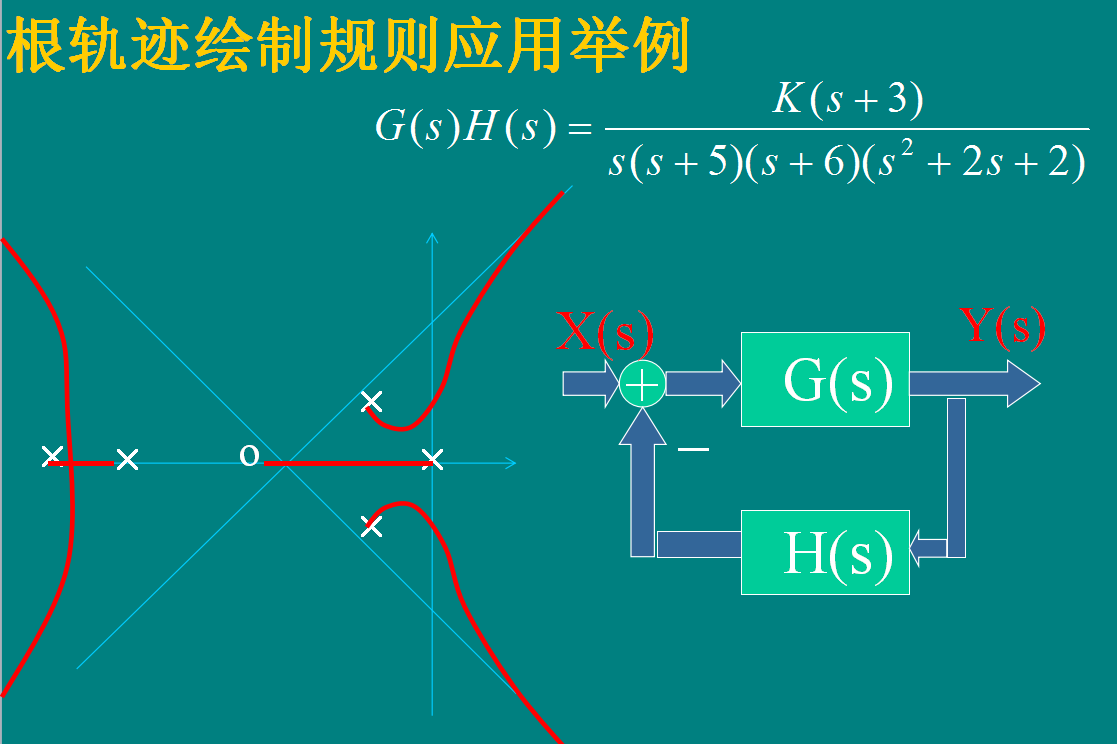
根轨迹绘制规则和方法

[规则1]   根轨迹与实轴对称

   证：特征根要么实根，要么为共轭复根，所以必与实轴对称。

方法：画一半即可

[规则2]：根轨迹起于开环极点，终于开环零点或无穷远点，且终于无穷点的分支数为n-m。

方法：从开环极点画起

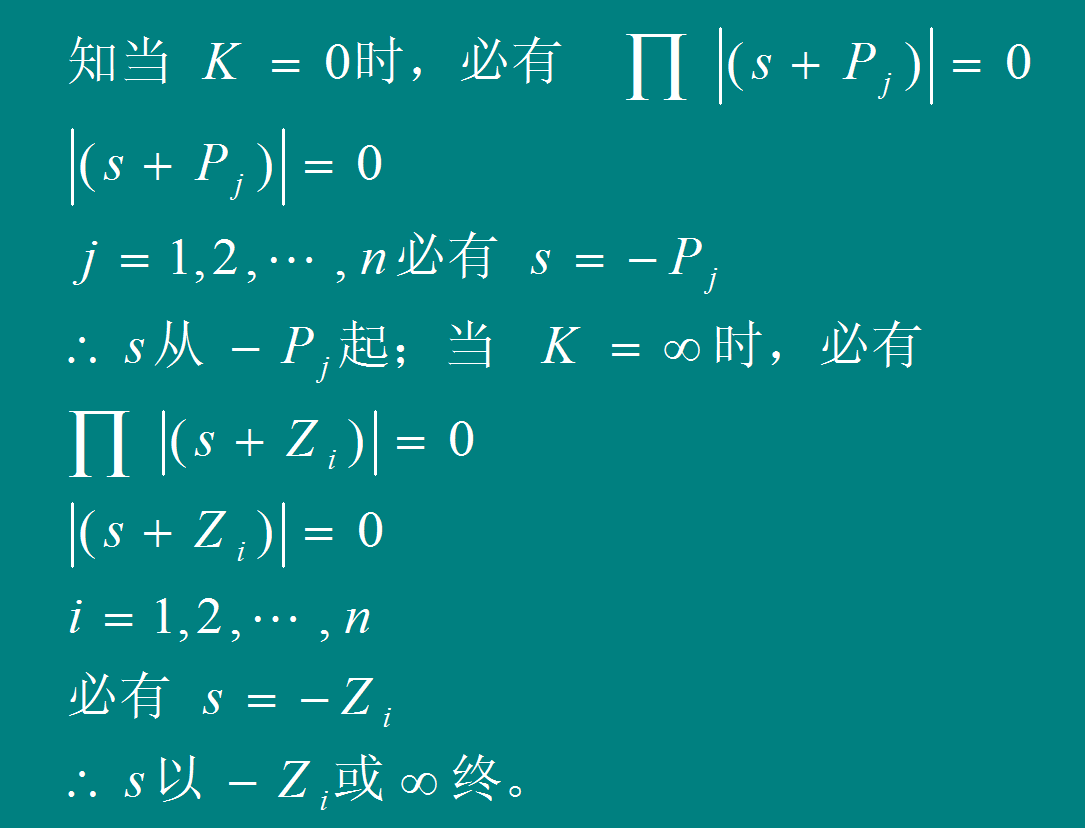
[规则3] 根轨迹分支数=n

证：n阶特征方程有n个根，K从0→∞时，n个根随之变化，故有n

条根轨迹。

方法：n阶系统有n条根轨迹

[规则4] 如果实轴上某一段右边的开环零点和开环极点总数为奇    数。则这一段就是根轨迹段（证明略）。

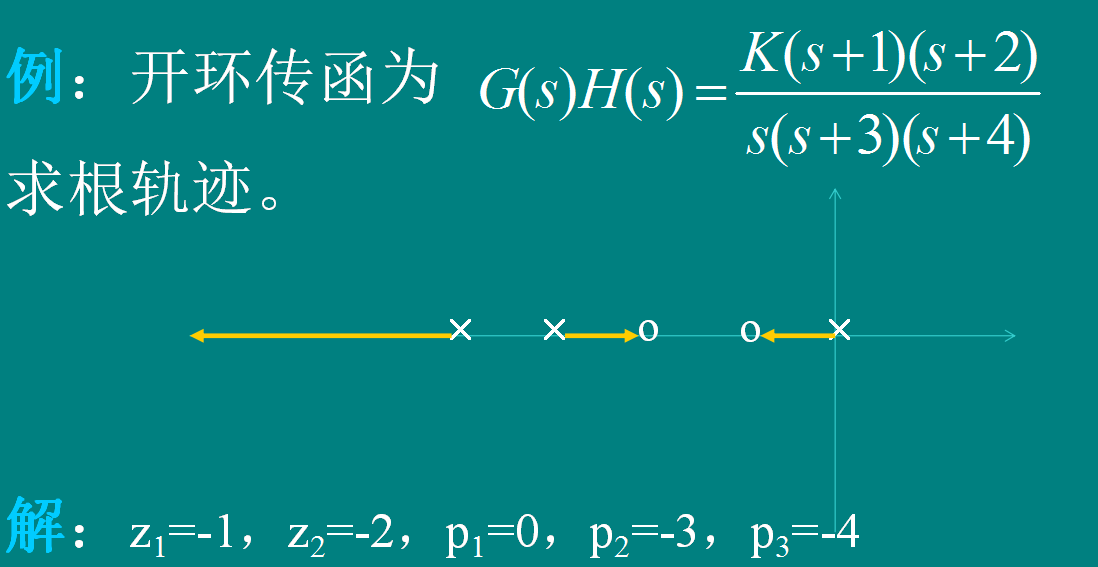
[规则5]有n-m条根轨迹分支沿渐近线趋于无穷远，其渐近线与正实轴的夹角为：

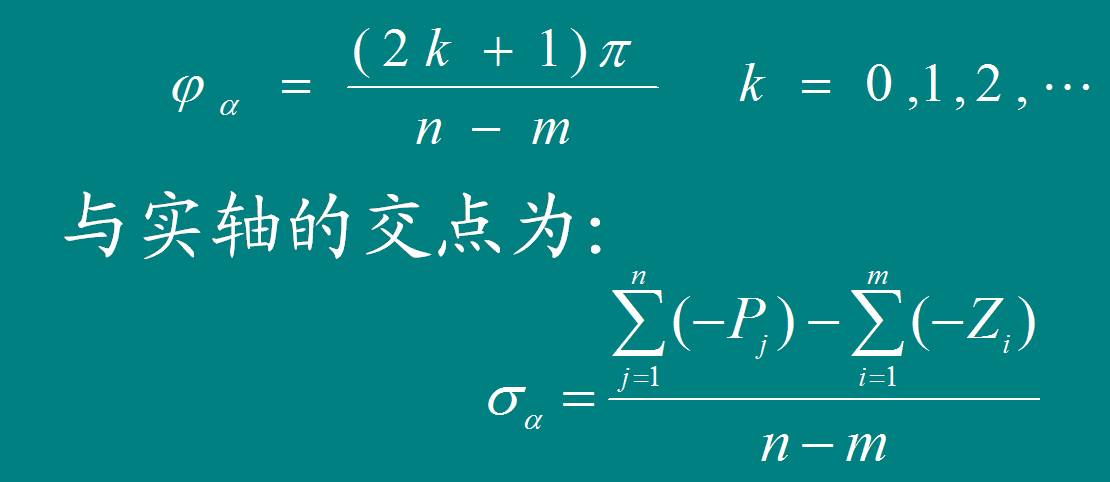
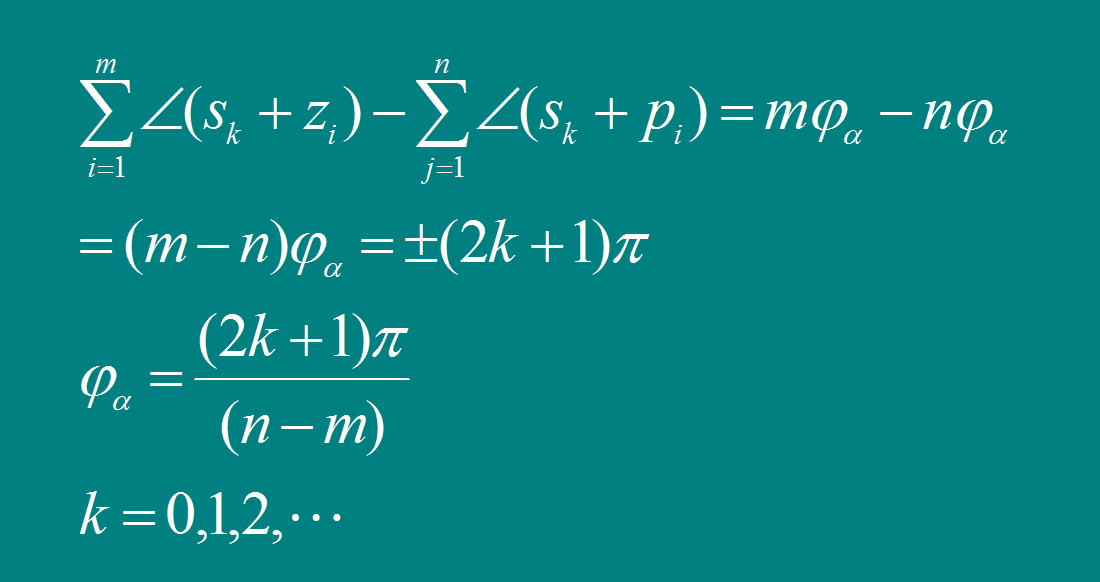
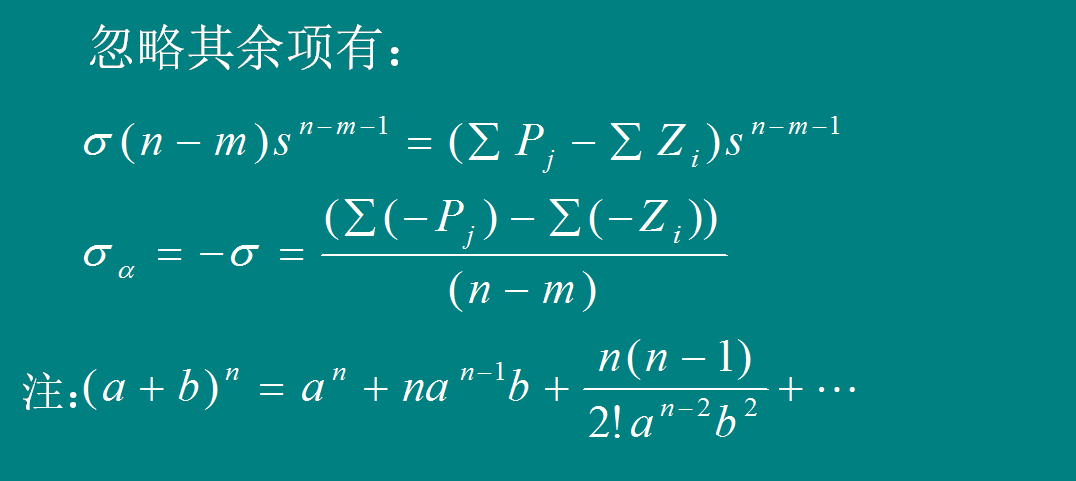
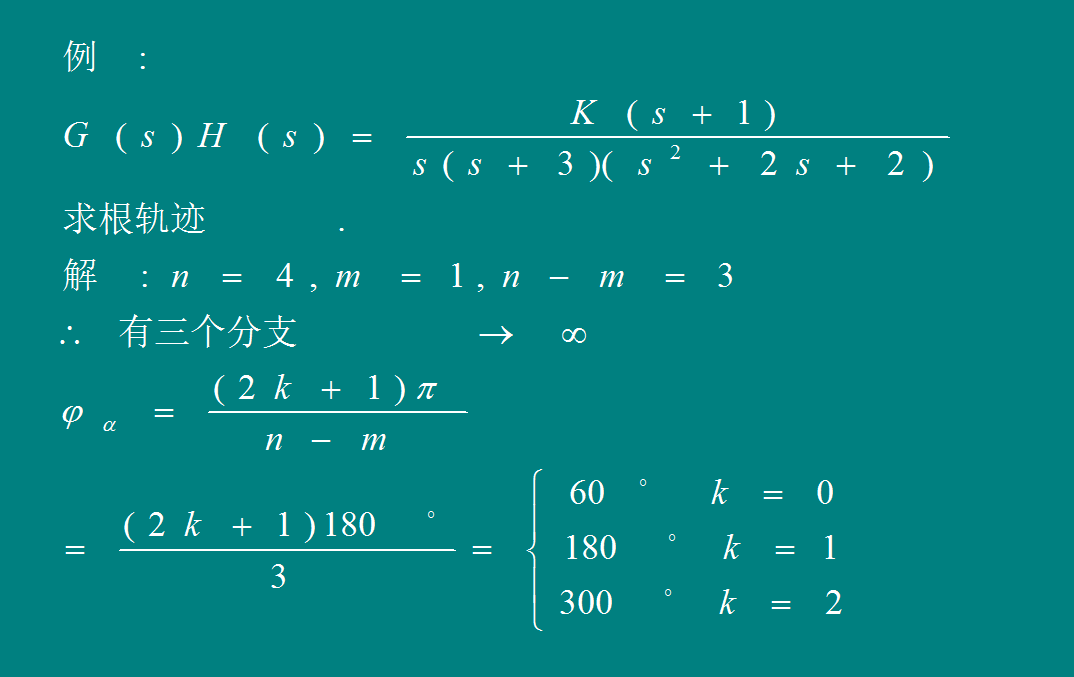
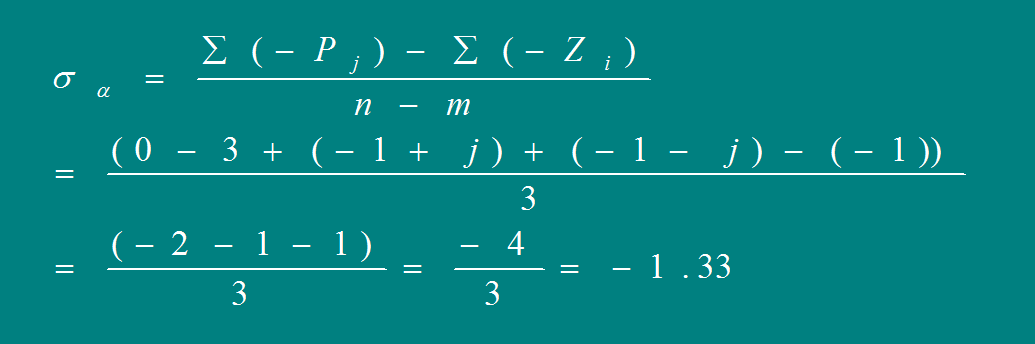
[规则6]  参见图4-18   起始（出射）角与终止（入射）角计算公式

限制条件：重零点或重极点，两点间零距离

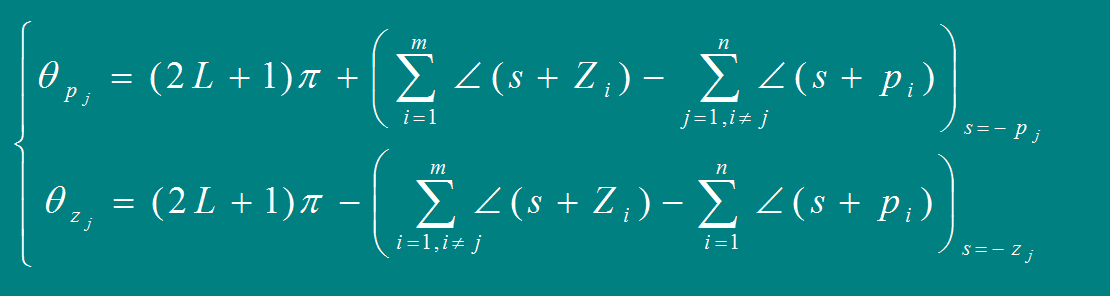
起始（出射）角为 

180度 + 至所有零点角和 - 至其他极点的角和

终止（入射）角为

180度 + 至所有极点角和 - 至其他零点的角和

     

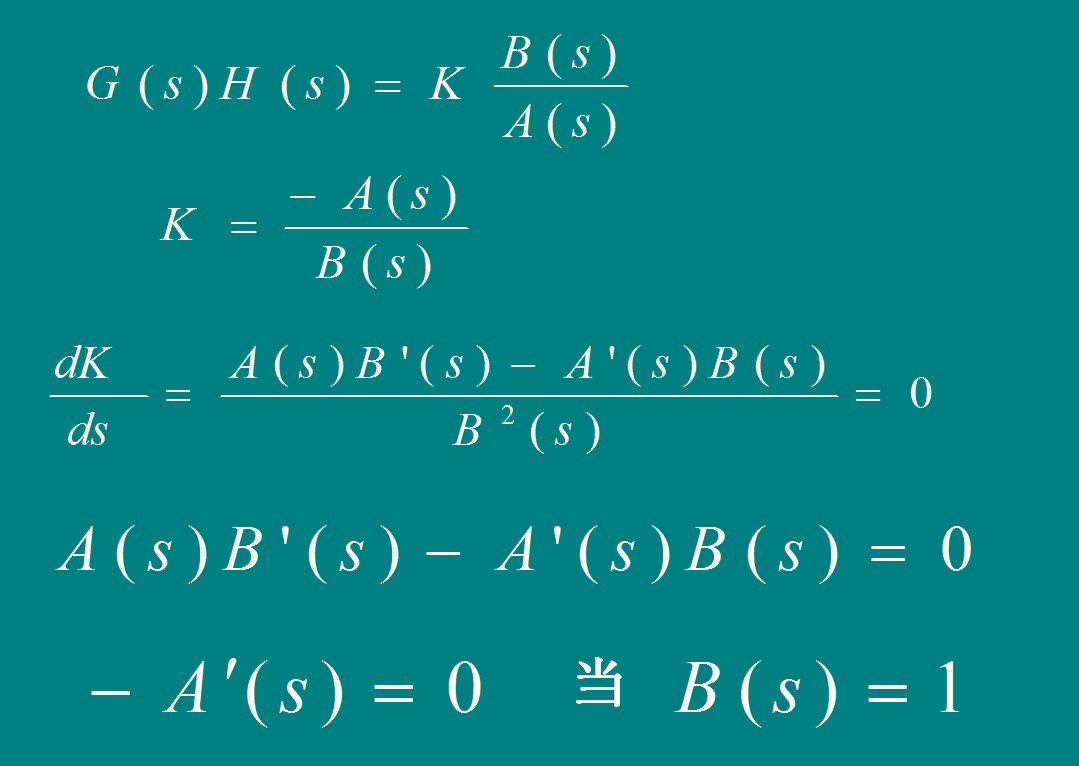
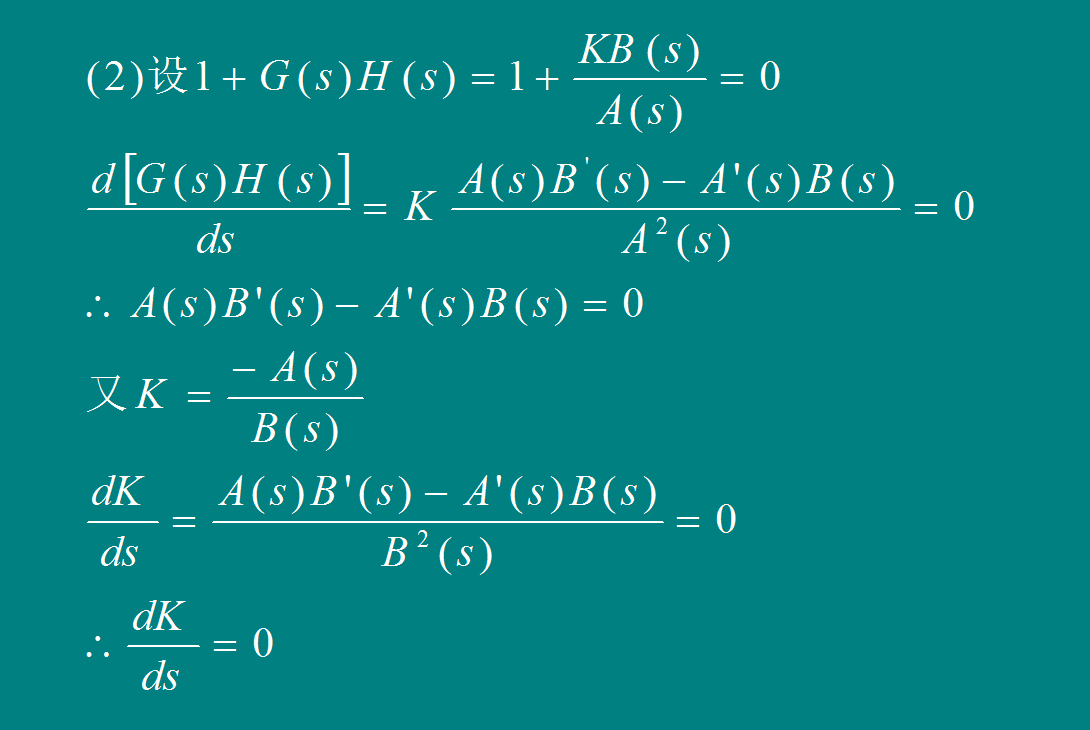
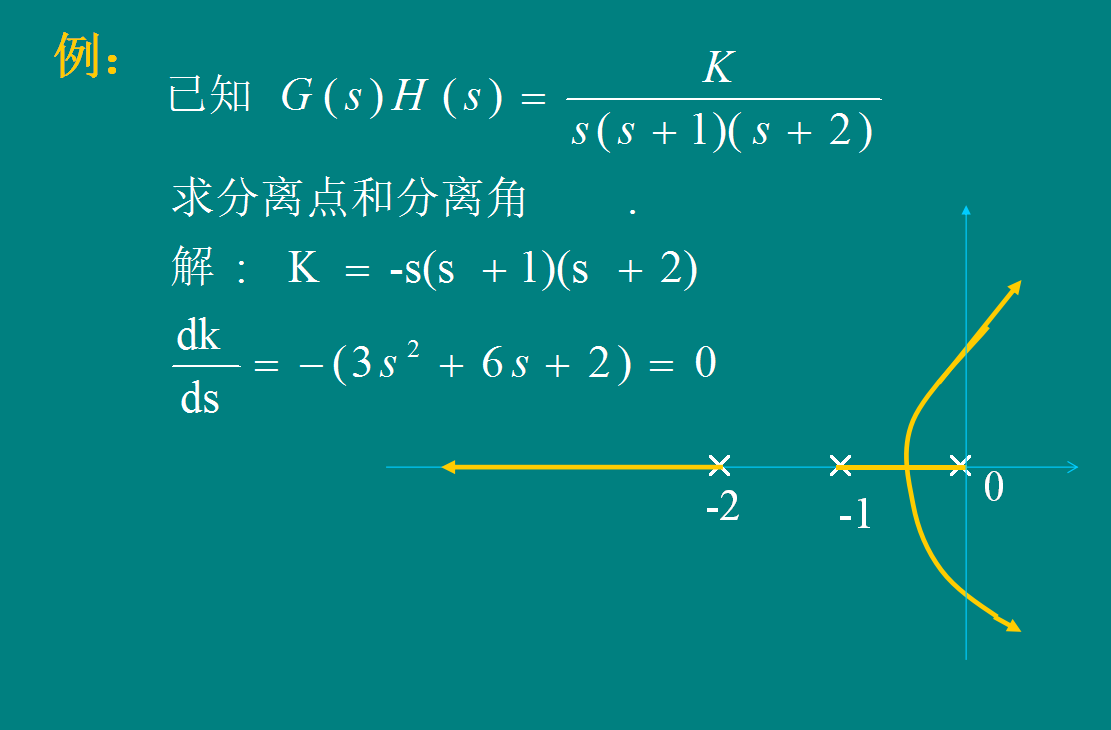
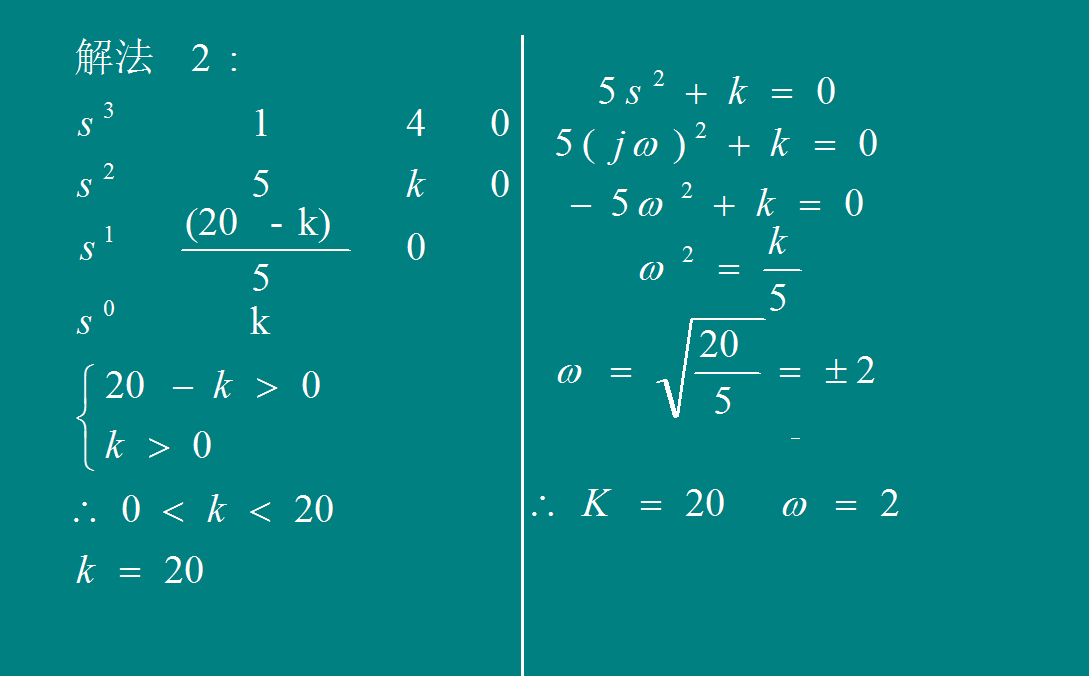
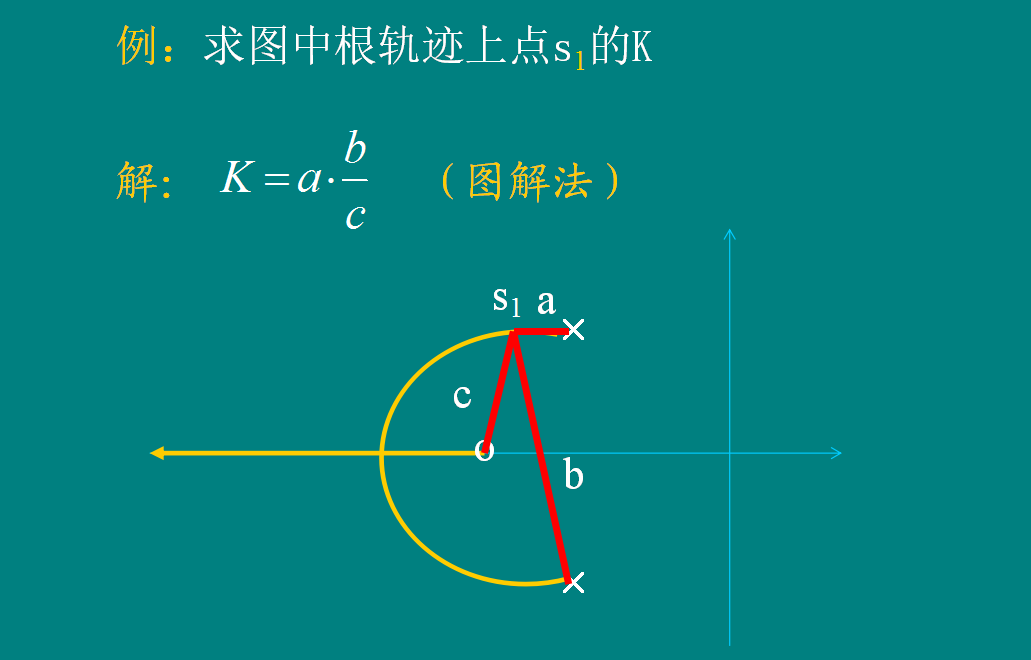
    根轨迹绘制规则和方法总结

[规则1] 与实轴对称

[规则2] 源于开环极点，终于开环零点，终于无穷远开环零点的    分支数为n-m。

[规则3] 分支数=n

[规则4] 如果实轴上某一段右边的开环零点和开环极点总数为奇    数。则这一段就是根轨迹段。

[规则5] 有n-m条根轨迹分支沿渐近线趋于无穷远，其渐近线与正实轴的夹角为

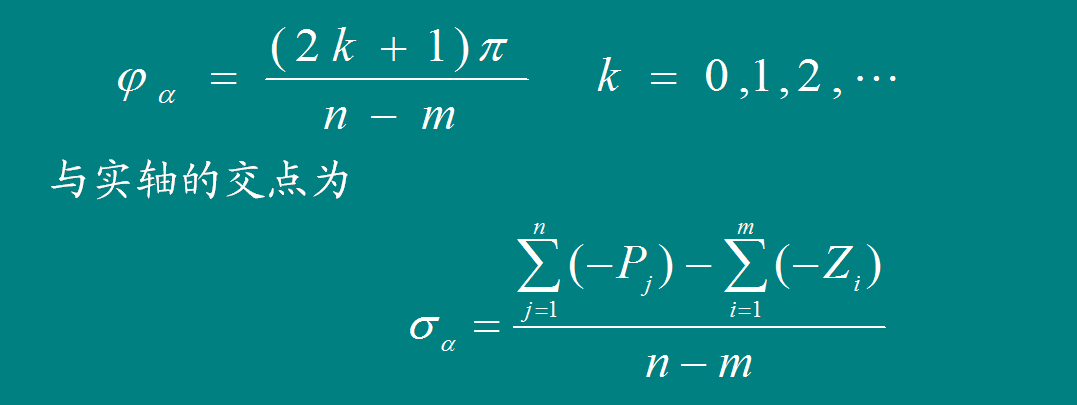
[规则6]

起始角与终止角计算公式

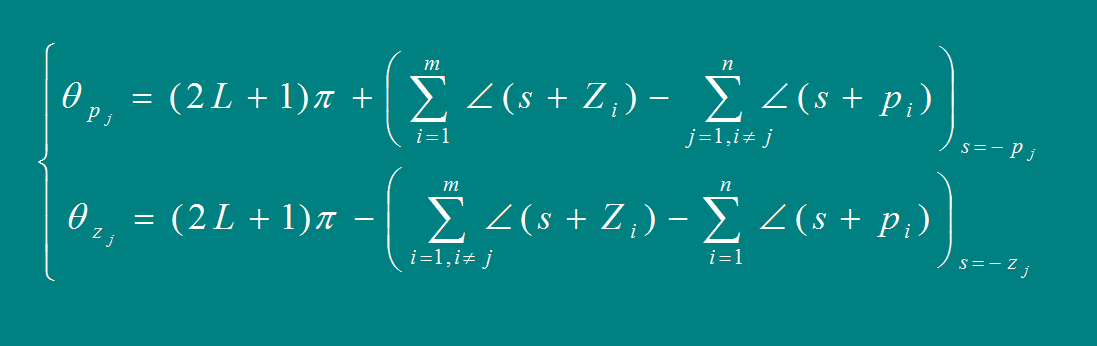
[规则7]

分离或会合角  的计算公式：