一、难度的意义
(一)难度
指试题的难易程度。 P=R/N
P代表试题难度;R为答对该试题人数;N为参加测验总人数
例:100人参加某一测验,其中第2题和第6题通过的人数分别为20人和30人,求第2题和第6题的难度。
这实际是以试题通过率作为难度指标的。这样计算所得难度值与试题实际困难程度是相反的。P在能力测验中通常需要一个反映难度水平的指标,在非能力测验中,类似的指标是“通俗性”,即取自相同总体的样本中,能在答案方向上回答该题的的人数。
(二)难度对测验的影响
1 、影响测验分数的分布形态
被全部考生都答错的试题,难度为0 ,所有考生全部得零分;被全部考生都答对的试题,难度为1.00 ,所有考生全部得满分。前者呈正偏态,后者呈负偏态。
(1)P值越小 →测验项目越难→测验分数集中在低分端→分数分布呈正偏态分布。
(2)P值越大→测验项目越易→ 测验分数集中在高分端→分数分布呈负偏态分布。
即:测验项目过分容易或过分难,都会造成测验分数偏离正态分布,而使测验分数的离散程度变小。
2、影响测验分数的离散程度
过难过易的测验,会使测验分数相对地集中在低分端和高分端,从而使分数的全距缩小。
3 、影响测验的鉴别能力
P值越接近0.50,试题的鉴别能力就越高;相反,P值越接近1.00或0,试题鉴别能力就会越低。
(三)测验的适宜难度
0.50是测验的适宜难度。有两层意思:一是测验中的各试题的难度;二是整个测验的平均难度。测验的试题,其难度在0.20-0.80之间,整个测验的平均难度又接近0.50附近,这个测验就具有适宜的难度。
二、难度的计算
(一)二分法记分项目的难度
1、通过率 P=R/N
2、极端分组法(上下27%)
具体步骤:(1)先依次测验总分的高低,按由高到低的顺序,依次排列试卷;(2)从得分最高的一份试卷开始依次向下选出全部试卷的27%,做为高分组;(3)从得分最低的一份试卷开始依次向上选出全部试卷的27%,作为低分组;
P=(PH+PL)/2
PH、PL分别为高分组与低分组的通过率
例:100人参加某测验,高分组与低分组各取27人,其中第一题高分组20人答对,低分组10人答对。这道题的难度系数是多少?
多项选择项目的难度校正:
CP=(KP-1)/ (K-1)
CP是校正后的通过率
P为实得通过率
K为备选答案的数目。
比如P为75%,5个备选时,CP为69%;4个备选时,CP为67%;3个备选时, CP为63%;2个备选时, CP为54%。
校正难度的作用
①检验实际难度
例: 某题通过率为75%,是一个五选一的题目。
②比较两个不同选项数题目的难度
例: 有二道题,一题的难度为0.50,有五个选项,另一题的难度为0.53,有四个选项。
(二)非二分法计分项目的难度
1、得分率法
例:某语文测验第五题的满分为12分,这道题考生的平均得分为8.5分,问该题的难度是多少?
2、极端分组法
用极端分组计算法计算主观性试题难度
具体步骤:(1)按测验得分排列试卷,确定高分与低分组,各占应考学生数的25%(方法与前相同);(2)分别为高分组,低分组编制每道试题的分析表。(3)按下列公式计算难度。
(公式)

其中,P为难度;XH为高分组得分总数;XL为低分组得分总数;N为应试总人数的25%;H为这道题的最高得分;L为这道题的最低得分。
下表是随机抽取22名被试在某数学测验中四道题目的得分情况,每题的满分分别为1分、2分、3分和4分,请分析其难度。
三、难度水平的确定
根据测验的目的、项目的形式和测验的性质来确定。
1、学业考试
目的是教学内容掌握的情况,所以只要认为内容是重要的,就可以选择,而不论难度。
2、人员选择:
采用难度值接近录取率的项目。录取率为40%,则理想的难度在0.40左右。0.50左右难度的题目,可以对全体被试作最大程度的区分。
例如:要从高中生中选拔15%的人参加全市的数学竞赛,则就应提高项目难度,使P值接近0.15。
3、对于选择题
难度值要大于概率。
如难度值等于或小于概率,如鉴别力好,通过者都是水平最高的,也可保留。
4、对于人格测验
人格测验的项目不存在难度问题,与此相应的指标叫通俗性,即同一类人在答案方向上回答 的人数,计算方法同难度计算方法。
四、难度的等距变换
(一)难度存在的缺陷
难度指标属于顺序变量,不具有相等的单位,所指出的仅仅是项目的相对难度。
例如:3个测题的难度指数分别为0.60、0.70、0.80。我们只能说:第一题最难,第二题次之,第三题最容易。虽然三题难度分别相差10%,但我们不能说第一题与第二题的难度之差等于第二题与第三题之的难度之差。通过率P无法指出难度之间差异大小,可见顺序性这一点,对我们作进一步的难度分析带来了困难,必须设法将它转换成等距量表。
(二)难度转化为Z分数
以项目的通过率来表示项目的难度,虽然计算方便,易于理解,但这类难度指标属于顺序变量,不具有相等的单位,所指出的仅仅是项目的相对难度。例如,3个测题的难度指数分别为0.60,0.70,0.80。
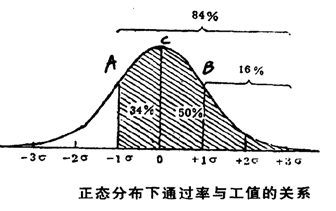
某项目A通过率为84%(P=0.84),那么这项目的难度为-1σ。
某项目B通过率为16%(P=0.16)则这个项目的难度为+1σ。
若某题C恰好有50%的人通过(P=0.50),则该题的难度为0。
较难的项目难度为正值,较易的项目难度为负值。
(三)难度转换为美国教育测量服务中心采用的难度指标
但是Z数有小数点和负值,所以表示难度也有不便之处,通常需要转换成另一种单位的等距量表。其中较为常用的是美国教育测量服务中心采用的难度指标:
以Δ作为难度指标 Δ=13+4Z
P = .0013 Z = +3 Δ= 25
P = .16 Z = +1 Δ= 17
P = .50 Z = 0 Δ= 13
P = .84 Z = -1 Δ= 9
P = .9987 Z = -3 Δ= 1
△值越大,则难度愈大,△值愈小,难度越低。
对一般教师来说,只要计算出P值即可。但如果要作更精确的统计分析,则就需要计算出具有等距量表性质的△值。


