一、信度与测量误差

（一）信度的含义

信度（reliability）指可靠性或可靠的程度。测验的信度则是指测验结果的可靠程度。换句话说，若能用同一测量工具反复测量某人的同一种心理特质，则其多次测量的结果间的一致性程度就叫信度。

一般说来，一个好的测量必须具有较高的信度，也即是说，一个好的测量工具，只要遵守操作规则，其结果就不应随工具的使用者或使用时间等方面的变化而发生较大变化。

（二）经典测量理论（CTT）的假设

ｘ＝Ｔ+Ｅ

T=V+I

ｘ＝V+I+Ｅ

X为实得分数   T为真分数 

E为随机误差分数

V为目标真分数  

I为非目标真分数（系统误差）

实测值是实际测量某种事物时所获得的测定值，也称实得分数或观察分数。真值是被测量的事物的真实规模的取值，也称真分数。实得分数和真分数之差称为测量误差或误差分数。实得分数由真分数和误差分数组成。其关系式为ｘ＝Ｔ＋Ｅ（其中，Ｘ为实得分数，Ｔ为真分数，Ｅ为误差分数）。Ｅ＝Ｘ－Ｔ，Ｅ是一个绝对数，可以称为绝对误差。绝对误差若为正值，则实得分数高于真分数，真分数被实得分数高估。绝对误差若为负值，则实得分数低于真分数，真分数被实得分数低估。若绝对误差的数值大，说明实测值（实得分数）与真值（真分数）相差较大，即测量结果的信度低或可靠性低。若绝对误差数值小，则信度高或可靠性高。

E=X-T

E>0    高估

E<0    低估

E=0    既不高估也不低估

实得分数的相对误差是误差分数（Ｅ）对于真分数（Ｔ）所占的百分数。即相对误差＝E/T×100%。

实际上，我们常常不知道真分数的取值。在不知道真分数取值的情况下，也可以用最大绝对误差（Ｅ）对于实得分数（Ｘ）所占的百分数来作为这个这个实得分数（Ｘ）的最大相对误差，即最大相对误差＝E/X×100%。

二、信度的统计定义

（一）经典测量理论假设的推论

在理论上，正的误差分数与负的误差分数相抵消，平均误差为０。根据这一假设，实得分数的方差应等于真分数的方差加上测量误差的方差。即S_X²=S_T²+S_E²  （其中，S_X²为实得分数的方差，S_T²为真分数的方差，S_E²为误差分数的方差。）

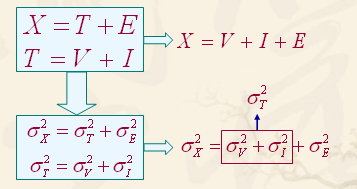
（二）信度的统计定义

S_X²=S_T² +S_E²

信度可定义为真分数方差与实得分数方差的比率。

即

r_XX= S_T²/ S_X²=（S_X²- S_E²）/ S_X²=1- S_E²/ S_X²

代表测量的信度

代表真分数的变异

代表总变异数，即实得分数的变异

真分数方差（S_T²）在实得分数方差（S_X²）中所占的比重越大，则信度（r_XX）就越高。

信度系数和信度指数    r_xx=r_xT²=S_T²/S_X²

信度指数的平方就是信度系数

测量标准误

信度系数越高，标准误越小；信度系数越低，标准误越大。

信度指统计量（如样本平均数）与参数（如总体平均数）的接近程度。

在统计学中统计量越接近参数，这个统计量的可靠性或信度越高。反之，如果统计量与参数相差很大，这个统计量的可信度便很低。

信度指一种测验对相同的应试者再次测验时引起同样反应的程度。

信度就是指各应试者两次测验分数或等级的前后一致的程度。如果两次测验的结果一致，则可认为测验结果的信度高；反之，若两次测验的结果不一致，则可认为测验结果的信度低。

三、描述信度的指标

信度系数是表示测量结果的稳定性程度的指标。记为：r_XX。 

心理测量书籍推荐