数学模型及其性能分析

如今，数学方法渗透并支配着一切自然科学的理论分支，它愈来愈成为衡量科学成就的主要标志了。合成生物学当然也不例外，在学习的过程中我们可能需要对问题建立合适的数学模型从而便于我们的分析，因而下面我们需要了解一下我们常用的数学工具。

一、   MATLAB

一、MATAB简介：

MATLAB（矩阵实验室）是MATrix LABoratory的缩写，是一款由美国The MathWorks公司出品的商业数学软件。MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。除了矩阵运算、绘制函数/数据图像等常用功能外，MATLAB还可以用来创建用户界面及与调用其它语言（包括C,C++,Java,Python和FORTRAN）编写的程序。

二、MATLAB工具箱：

       MATLAB的一个重要特点是可扩展性。作为Simulink和其它所有MathWorks产品的基础，MATLAB可以通过附加的工具箱（Toolbox）进行功能扩展，每一个工具箱就是实现特定功能的函数的集合[b]。MathWorks提供的工具箱分以下几大类：

 

    数学和优化

    统计和数据分析

    控制系统设计和分析

    信号处理和通讯

    图像处理

    测试和测量

    金融建模和分析

    应用程序部署

    数据库连接和报表

    分布式计算

 

这些工具箱大多是用开放式的MATLAB语言写成，用户不但可以查看源代码，还可以可根据自己的需要进行修改以及创建自定义函数。此外，常有用户在MATLAB Central: File Exchange发布自己编写的MATLAB程序或工具箱，供他人自由下载使用。

三、MATLAB语言：

MATLAB语言是一种交互性的数学脚本语言，其语法与C/C++类似。它支持包括逻辑（boolean）、数值（numeric）、文本（text）、函数柄（function handle）和异素数据容器（heterogeneouscontainer）在内的15种数据类型，每一种类型都定义为矩阵或阵列的形式（0维至任意高维）[8]。

 

执行MATLAB代码的最简单方式是在MATLAB程序的命令窗口（Command Window）的提示符处（>> ）输入代码，MATLAB会即时返回操作结果（如果有的话）。此时, MATLAB可以看作是一个交互式的数学终端，简单来说，一个功能强大的“计算器”。MATLAB代码同样可以保存在一个以.m为后缀名的文本文件中，然后在命令窗口或其它函数中直接调用。

1、变量与赋值：

MATLAB的变量名字跟许多程序语言一样，严格区分大小写，例如，var、VAR和Var是三个不同的变量。另外，MATLAB中变量名字必须以字母为首字母，3var、_var等是非法的变量名。 变量由赋值运算符（=）定义. MATLAB是动态检查的，这意味着变量可以在未定义其类型的情况下赋值并且变量的类型也可以改变，除非将变量看做是符号对象[9]。变量值可以取自常量，计算中的其他变量的值，或某一函数的输出。例如：

 

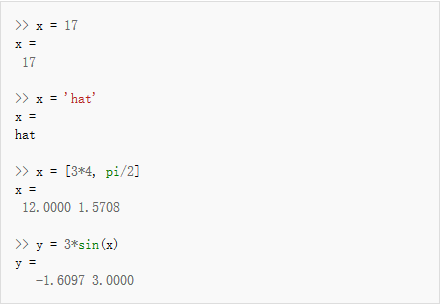
2、矢量和矩阵：

 

MATLAB的意思是"矩阵实验室"，因此它提供了许多创建矢量，矩阵和多维数组的便捷的方式。在MATLAB自己的语言中，一个矢量（vector）指的是一维（1×N或N×1）矩阵，在其他语言中通常被叫做数组（array）。 矩阵（matrix）通常指的是2-维数组，例如m×n数组其中m和n大于或等于1。多维数组通常指的是维数大于2的数组。

 

需要注意的是，虽然MATLAB用C语言重写，但是在矩阵存储方式上却和FORTRAN保持一致，两者使用的均为列优先存储，而非行优先存储[c]。在进行较大的矩阵运算时，这一差别对性能的影响是不应忽略的。

 

MATLAB提供了定义简单数组的简单方式，使用语法: 初值:增量:终值。例如:

 

定义了一个名为array的变量(或向已存在的变量array赋予一个新值)，其值为包含1,3, 5, 7, 9的一个矢量。即数组由1开始（初值），每次以增量2 (增量)递增，当达到9 (终值)时停止。

在该语法中增量可被省略（这样仅剩一个冒号），这时增量采用默认值1。

 

由于默认增量为1，上面的语句对变量ari用1, 2, 3, 4, 5的矢量赋值。

在MATLAB内定义矩阵同样很简单，例如：

在MATLAB内存取矩阵元素同样非常简单，例如：

 

若要对矩阵内所有元素做同样的运算，如次方倍，则需要在运算对象前面加上"."，例如：

 

 

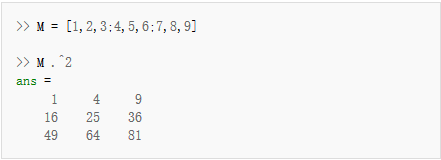
若不在运算对象前面加上"."则代表矩阵运算：

 

3、代数/符号运算：

 

利用MATLAB的符号数学工具箱（SymbolicMath Toolbox）[d]可以进行代数或符号运算，如分解多项式因子和解代数方程：

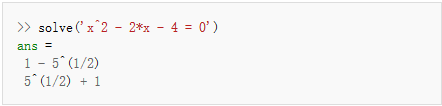
4、图形图像：

MATLAB中常用的绘图命令是plot，例如描绘一个在[-4,4]区间内的正弦函数：

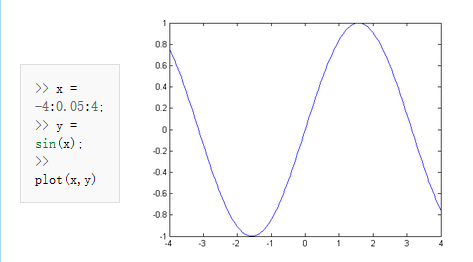
利用plot命令也可以在同一幅图中描绘多个函数图形：

用MATLAB的画图命令可以生成复杂的三维图形[e]：

二、   Mathematica

一、Mathematic简介：

Mathematica是一款符号计算软件，有时候也被称为计算机代数系统，广泛使用于科学、工程、数学、计算等领域。

 

它是由英国科学家斯蒂芬·沃尔夫勒姆提出构想，并且由他所领导的沃尔夫勒姆研究公司（位于美国伊利诺伊州香槟市）开发的一款广泛使用的科学计算软件。它拥有强大的数值计算和符号运算能力。它是目前为止使用最广泛的数学软件之一。

1. 二、       Mathematic功能：

Mathematica的功能包括：

• 各种基本数学函数库

• 各种特殊属性函数库

• 矩阵和数据操纵工具，包括对稀疏矩阵的处理

• 支持复数、任意精度数、区间算术和符号运算

• 2维和3维数据以及函数的可视化和动画工具

• 求解方程组、常微分方程、偏微分方程、微分代数方程、时滞微分方程、递推关系式等等

• 离散和连续微积分的数值和符号工具

• 多变量统计程序库，包括支持100多种数据分布的数据拟合、假设检验、概率和期望的运算

• 对运算和应用程序添加用户界面的各种工具包

• 约束和非约束以及局部和全局的最优化技术支持

• 程序语言支持：过程式编程语言、函数式编程语言和面向对象的编程语言

• 图像处理工具^[10]，包括图像识别

• 提供用于图论中图的分析和可视化的工具

• 分析组合问题的工具

• 用于文本挖掘的工具

• 数据挖掘的工具，比如聚类分析、字符串对齐和模式匹配

• 数论函数库

• 金融运算的工具，包括期权、债券、年金、派生工具等的计算

• 群论函数

• 技术文本处理，包括公式编辑器和自动报告生成

• 用于声音、图像和数据的小波分析程序库

• 控制系统程序库

• 连续和离散的积分变换

• 导入和导出数据、图像、视频、GIS、CAD^[11]等各种文件格式，并支持对生物医学类数据的输入和输出

• 链接Wolfram Alpha的大量数学、科学、社会经济学类的数据集合

• 查看并且重新使用前面的输入和输出（包括图像和文本记号）的笔记本界面

• 和基于DLL、SQL、Java、.NET、C++、FORTRAN、CUDA、OpenCL以及http的系统相链接的工具

• 编写并行程序的工具

• 当与互联网连接时，在笔记本中可同时使用“自由格式语言输入”（一个自然语言型的用户界面）^[12]和     Wolfram 语言

1. 三、       简单功能介绍：

1、算术计算：

Mathematica最简单的用法就是像计算器一样输入您的算式，然后按Shift+Enter。

和别的计算机语言一样，Mathematica分别用+、-、*、/、^来表示加、减、乘、除、幂，用圆括号(和)来控制运算顺序。此外，乘法也可以用空格表示：

在Mathematica中，数的大小和精度是不受限制的[2]，比如说我们可以计算100的阶乘：

Mathematica把不带小数点的数都当成精确值。一般情况下，当您输入的数字都是精确值时，输出也将是精确值：

只要输入的数当中有一个带有小数点，比如说，把“1”改成“1.”，Mathematica就会把它当成近似值，这样输出的也将是近似值：

2、使用函数：

当我们要进行复杂一点的计算时，就要用到数学函数了。与我们平时写数学公式的习惯不同，Mathematica中函数的自变量都括在方括号中，这样是为了与控制运算顺序的圆括号相区别。比如说计算4的算术平方根，就要用到表示平方根的函数Sqrt：

同样，我们也能计算2的算术平方根：

这看起来有些奇怪，它好像什么都没算。事实上，我们前面已经说过，当您输入的数字都是精确值时，输出也将是精确值。

Mathematica中大小写是严格区分的，Mathematica内建的函数首字母都是大写。除了一些一些常见的数学常数在Mathematica也用首字母是大写的符号来表示，如Pi表示圆周率、E表示自然对数的底、I表示虚数单位。这都和我们平常写数学公式的习惯不同。

这就是著名的欧拉恒等式，

下表列出了一些常用的数学函数：

Mathematica内建的数学函数非常丰富，涉及到数学的各个不同领域。最新版本的Mathematica中数学函数的全表可以参见Mathematica帮助中的Mathematical Functions。

3、代数运算：

Mathematica是一个计算机代数系统，它的强项就是代数运算。 比如说，您可以（在没有给a赋值的情况下）输入a+a。在一般的计算机语言中，这样输入可能会导致错误，因为您没有告诉计算机a是多少。但是，只要学过一点初等代数，我们不需要知道a的值也能知道a+a等于2a。在Mathematica中也是如此：

Mathematica中变量的符号不仅可以是英文字母，还可以是希腊字母，甚至别的符号，或者符号的组合：

与代数运算有关一个很有用的Mathematica函数是Simplify。事实上，Mathematica很懒，一般的式子它不会自动帮您化简，只会做一下调整顺序、合并同类项之类的工作。例如：

而Simplify则能够帮我们化简这些式子：

Simplify有时不能把式子化到最简。Mathematica提供了另一个函数FullSimplify，它化简式子时运用的变换规则比Simplify更多，化简能力比Simplify更强，但花的时间比Simplify要长。

4、输出近似值：

前面说过，当您输入的数字都是精确值时，输出也将是精确的。如果我们希望Mathematica输出的结果是近似值，可以在输入的末尾加上//N：

“//N”这种奇怪的写法其实是使用N这个函数时的另一种写法^[4]，Sqrt[2]//N就相当于N[Sqrt[2]]:

N是表示数值（也就是近似值）的函数。N[expr]表示表示expr的近似值，N[expr, n]表示expr的有n位精度的近似值。比如说，求圆周率的前100位：

 

 

以上便是对我们学习课程中可能用到的数学工具的一些简单介绍，希望能对你有所能帮助！