实验内容：

（1）命令的使用

1、 特征多项式的建立与特征根的求取

      在命令窗口依次运行下面命令，并记录各命令运行后结果

num1=[10];

den1=conv([2 1 0],[3 1]);

num2=[1 6];

 den2=conv([1 1] ,[1 5]);

[ num,den]= feedback(num1,den1,num2,den2,-1)

r=roots(den)                    

2、 传递函数零、极点的求取

在命令窗口依次运行下面命令，并记录各命令运行后结果

num=[6,0,1];den=[1,3,3,1];      构建传递函数的特征多项式

z=roots(num) ;                                 求零点

p=roots(den) ;                                 求极点

printsys(num,den)                               输出以多项式表示的传递函数

pzmap(num,den),title(‘极点－零点图’)              输出传递函数的极点和零点图。

（二）典型环节的验证

已知输入信号是单位阶跃信号，求以下典型环节的输出响应，分析其输入输出信号的变化关系。

1）、比例环节      G1(s)=1和G2(s)=2

2）、积分环节      G1(s)=1/s和G2(s)=1/（0.5s）

3）、含有惯性的微分环节 G1(s)=(s+2)/(0.01s+1)和G2(s)=(s+4)/(0.1s+1)

4）、惯性环节      G1(s)=1/(s+1)和G2(s)=1/(0.5s+1)

5）、比例积分环节（PI）G（s）=1+1/s和G（s）=2（1+1/2s）

6）、振荡环节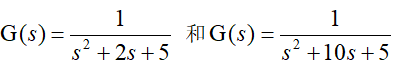   

写出以上典型环节的传递函数，并计算其单位阶跃响应，观察其输入输出信号的变化。

实验报告请在作业中提交，提交前请仔细查看实验报告的要求。