特性:
每个参与人对博弈信息有完全的了解,即掌握博弈规则、博弈过程及博弈各方的策略及收益,但不知道其他人的行动。
所有参与人同时决策且只决策一次(一次博弈)。
不管是否沟通过,都无法做出有约束力的承诺(非合作)
“划线法”是求解完全信息静态博弈均衡的常用方法。 通常说来,完全信息静态博弈都存在纳什均衡
纯策略纳什均衡
混合策略纳什均衡
一、存在一个纳什均衡的博弈
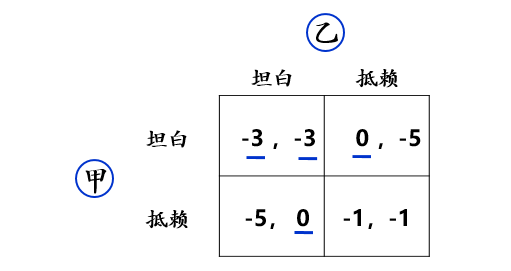
如果单元格里面的两个收益被同时划线,该收益所对应的策略组合即为纳什均衡。
求解得,囚徒困境中甲乙二人的纳什均衡为(坦白,坦白)
练习:价格战
假设彩电市场有两个寡头A、B,均面临降价与不降价的选择
若一方降价而另一方不降价,则降价的一方扩大了市场,赢利增加80个单位,不降价的一方市场缩小,赢利增加-100个单位;
若双方都选择不降价,则都保持原来的销售利润,增加的利润均为0;
若双方都选择降价,则各自增加-50个单位的赢利。
用划线法求解该博弈模型的纳什均衡。
二、存在多个纳什均衡的博弈
案例:情侣博弈
一对热恋中的情侣,展开了一场温情笼罩下的“博弈”:
• 如果男方看足球,女方独自去看演唱会,因为两人分开,双方的满意度都为0;
• 如果男方去看演唱会,女方看足球,因为两人分开,双方的满意度都为-1;
• 如果两人一起看足球,男方的满意度为2,女方的满意度为1;
• 如果两人一起看演唱会,女方的满意度为2,男方的满意度为1;
请用“划线法”寻找“情侣博弈”的纳什均衡
答案:

经划线法求解,男女双方的策略组合(足球,足球)和(演唱会,演唱会)均为该博弈的纳什均衡。
练习:斗鸡博弈
两只实力相当的斗鸡狭路相逢,每只斗鸡都有两个选择,后退或进攻:
如果两只斗鸡都进攻,结果两百俱伤,双方的收益均为-2;
如果一方进攻,一方后退,进攻的斗鸡获得的收益为1,后退的斗鸡因损失了面子,获得的收益为-1
如果两只斗鸡都后退,两者的收益均为-1。
请用“划线法”寻找“斗鸡博弈”的纳什均衡。
三、无法通过“划线法”找到纳什均衡的博弈(以石头、剪刀、布博弈为例)
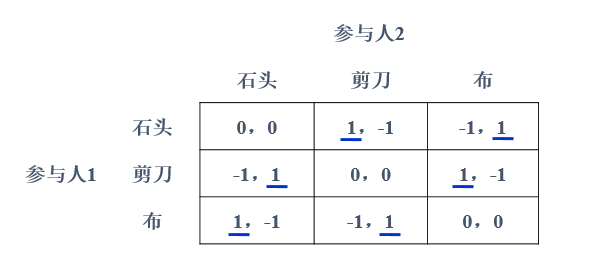
通过“划线法”求解,未找到“石头、剪刀、布”博弈的纳什均衡。该博弈又为完全信息静态博弈,故该博弈存在混合策略的纳什均衡。
完全信息静态博弈,
可能存在一个或多个纯策略纳什均衡
如果不存在纯策略纳什均衡,则一定存在混合策略纳什均衡
混合策略均衡指博弈参与者以一定的概率分布随机选择策略中的策略,使得其他博弈参与者在各个可能的策略之间无差异。


