博弈的表示方法
-
1
-
2
上一节
下一节
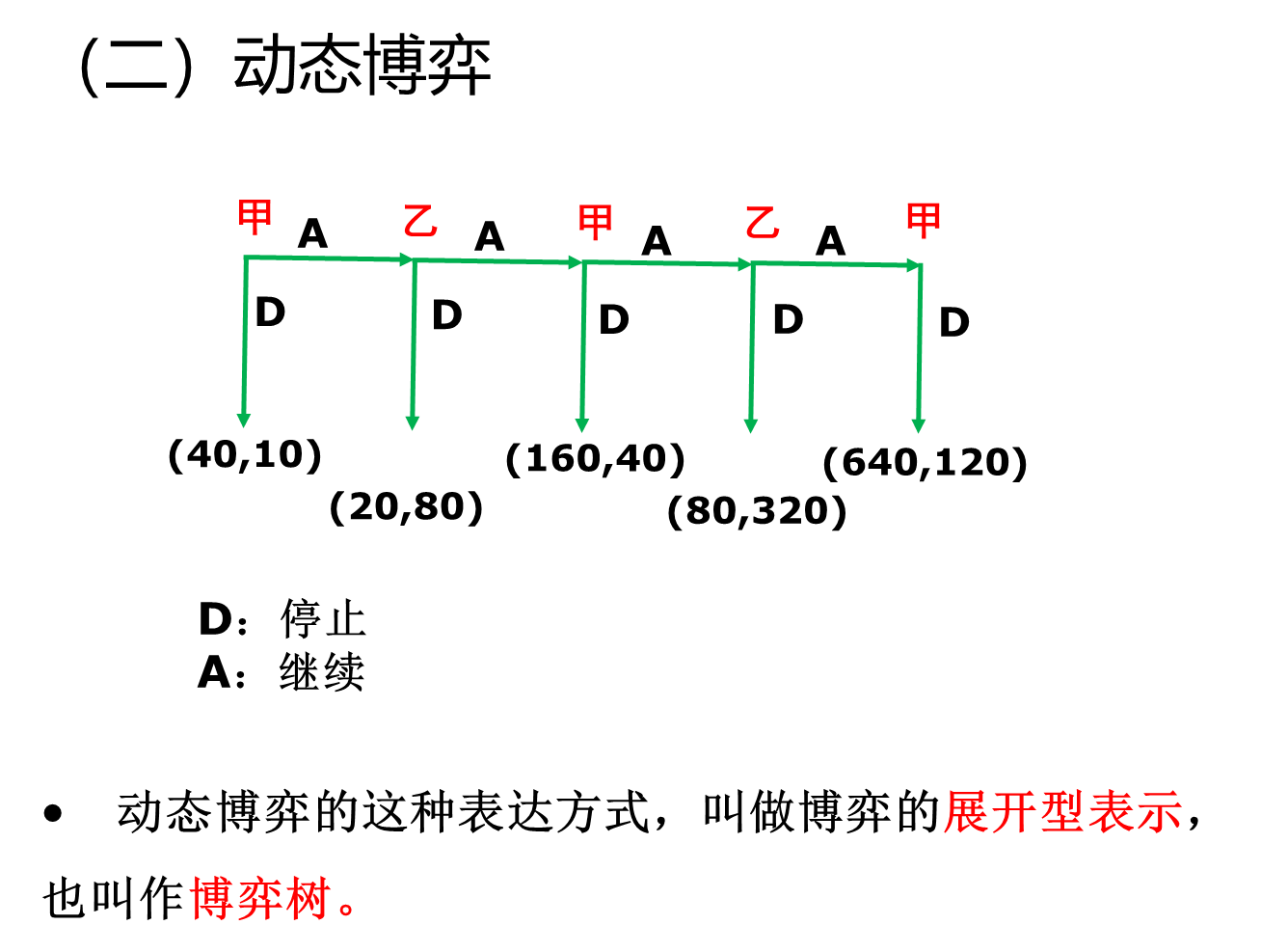
(一)静态博弈
l如果将“石头、剪刀、布”博弈的收益用数字表示:
Ø“1”表示“赢”
Ø“0”表示“平局”
Ø“-1”表示“输”

上述矩阵,叫做支付矩阵
静态博弈的这种表达方式,叫做博弈的矩阵型表示
例1:价格战
故事模型
假设彩电市场有两个寡头A、B,均面临降价与不降价的选择
Ø若一方降价而另一方不降价,则降价的一方扩大了市场,赢利增加80个单位,不降价的一方市场缩小,赢利增加 -100个单位;Ø若双方都选择不降价,则都保持原来的销售利润,增加的利润均为0;Ø若双方都选择降价,则各自增加-50个单位的赢利。
问题:写出该博弈模型的矩阵型表示
| 寡头A | |||
| 降价 | 不降价 | ||
| 寡头B | 降价 | -50,-50 | 80,-100 |
| 不降价 | -100,80 | 0,0 | |
例2:猎鹿博弈
设想村庄里有两个猎人,他们的主要猎物只有两种:鹿和兔子。
l如果两个猎人齐心合力,他们就可以共同捕得一头鹿,两人平分后,可供每人吃10天。
l如果两个猎人各自行动,
Ø分别去打兔子,每人只可以抓住4只兔子,4只兔子可以供一个人吃4天;
Ø一人去打兔子一人去捕鹿,则前者收益为4,后者收益为0。
| 乙 | |||
| 鹿 | 兔 | ||
| 甲 | 鹿 | 10,10 | 0,4 |
| 兔 | 4,0 | 4,4 | |