一、模型概述

“酒吧问题”是斯坦福大学的阿瑟(W.B.Arthur)教授1994年在《美国经济评论》发表的一篇文章中提出来的。它是在博弈论的基础上发展起来的一个理论模型。

理论模型

–  假设一个小镇上总共有100人。这些人在每个周末，都要决定是去酒吧活动还是待在家里休息。

–  酒吧的容量是有限的，如果去的人多了，去酒吧的人会感到不舒服。此时，他们留在家中比去酒吧更舒服。

–  假定酒吧的容量是60人，如果某人预测去酒吧的人数超过60人，他的决定是不去，反之则去。

 这100人该如何作出选择呢？

这是典型的动态群体博弈问题。模型假设条件：

• 每一个参与者只能根据以前的历史数据归纳出此次行动的策略，没有其他的参考信息

• 互相之间没有信息交流

二、阿瑟的两种考察方法

1.  计算机模拟实验

Ø 起初，去酒吧的人数没有一个固定的规律

Ø 经过一段时间后，去与不去的人数之比接近于60：40。尽管每个人不会固定地属于去或不去的人群，但此系统的这个比例是不变的。

Ø 自组织的形成一个生态稳定系统

（2）阿瑟教授对真实人群的考察

 

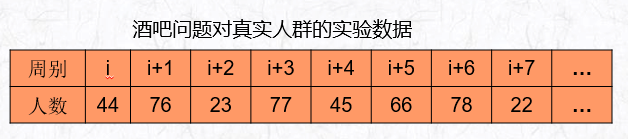
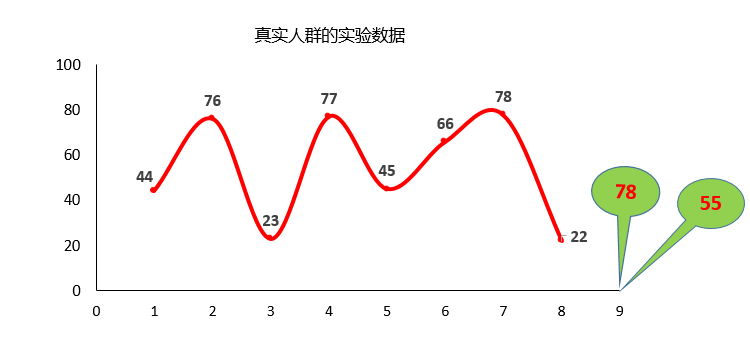
结论：实验对象的预测呈有规律的波浪形态。但后来的学者已经用实验证明这个预测在多数情况下是不正确的。

三、“酒吧问题”小结

该预测是一个非线性的过程

–所谓非线性的混沌系统，可以理解为2是1的两倍，但是100万却不是1的100万倍

–人们根据历史数据来预测以后去酒吧的人数

–历史数据是“任意的”

–未来不可能得到一个确定的值

 

相关案例

–  股市的钱都被谁赚走了？

–  凯恩斯的“选美理论”

–  高考报志愿博弈

这些问题都是“酒吧博弈”模型的延伸，被统称为“少数者博弈”。

四、“酒吧博弈”的启示

•    从一个非线性系统的整体来说，其变化往往是不可预测的。在非线性的混沌系统中，临界点对于策略思维具有极大价值。

•    由于混沌系统的过程无法预测，但也可以采取恰当的策略来达到个体最优。在这样的策略中，少数者策略是值得我们重点关注的。