引入——秦宣太后的遗命（10分钟）

战国时，秦宣太后快要病死的时候，拟了一条遗命：“如果我死了，要用魏丑夫为我殉葬。”魏丑夫知道后坐卧不宁。一个叫庸芮的大臣出面为魏丑夫劝说太后。

•   庸芮说：“太后您认为人死后，冥冥之中还能知觉人间的事情吗？”

•   太后说：“人死了当然就什么也不知道了。”

•   庸芮又说：“像太后这样圣明，明知道人死了不会有知觉，为什么还要平白无故的把自己心爱的人置于死地呢？倘若人死了还知道什么的话，那么先王这几十年来，在地下怒火不知道已经积累了多少。太后您去了阴世，补过还来不及，哪还有机会与魏丑夫寻欢作乐？万一让先王看见了魏丑夫，岂不是更要惹出大麻烦来？”

太后想了想，就断了用魏丑夫殉葬的念头。

 

总结：

庸芮用假设前景，向回推导，说明将魏丑夫殉葬的不明智。他知道太后已经被爱情烧的发昏，正常的道理是听不进去的，只有用这种“危险”的提示，才能让她有所醒悟。

这种方法，在博弈论中叫做“倒推法”

–  在动态博弈（相继行动的博弈）中，每个参与者都必须向前展望或预期，来估计对手的意图，从而倒后推理，决定自己这一步该如何行动。

–  线性思维链：假如我这么做，我的对手会怎么做，若是那样，我应该这样应对……

简而言之，通过“向前展望——倒后推理”的法则，找出最优策略。

蜈蚣博弈及其悖论（20分钟）

1. 蜈蚣博弈由来

    蜈蚣博弈是由罗森塞尔(Rosenthal)在1981年提出的一个动态博弈问题。

2. 模型描述

   两个参与者A、B轮流进行策略选择，可供选择的策略有“合作”和“背叛” 两种。

–  规则是：A、B两次决策为一组，第一次若A决策结束，A、B都得n；第二次若B决策结束，A得n-1，而B得n+2；

–  下一轮则从A、B都得n+1开始。

博弈展开式如下（假设n=1，博弈次数为10）：                             

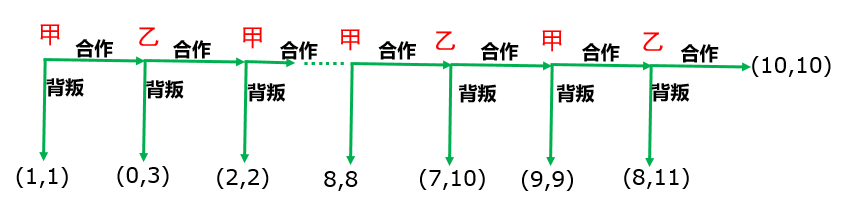
由于这个博弈的展开型像一条蜈蚣，因此被称为“蜈蚣博弈”。现在的问题是：A、B是如何进行策略选择的呢？

结论：在第一步A将选择“背叛”！

思考：难道蜈蚣博弈的倒后推理法存在问题？

从逻辑推理来看，倒推法是严密的，但结论是违反直觉的，这种现象，就叫做“蜈蚣博弈悖论”。

例:向邻居借斧头的故事

学者用科学的方法推导出：倒推法是分析完全且完美信息的有用工具，也符合人们的直觉，但在某种情况下却存在无法解释的缺陷。