课前学习任务

若二次曲面方程经平移和旋转变换化成了  的形式，则曲面本身的的形状并未改变. 如果再考虑伸缩变换

相当于曲面方程中的系数 a, b, c 发生了伸缩，而曲面的形状虽有所改变，但曲面的“类型”不会变，如以下例子所示.

例1：令 a, b 在 1 和 4 之间变化，c 在 -1 和 -4 之间变化.

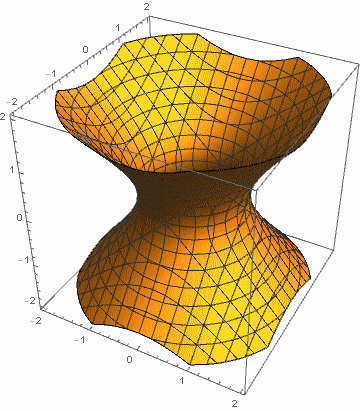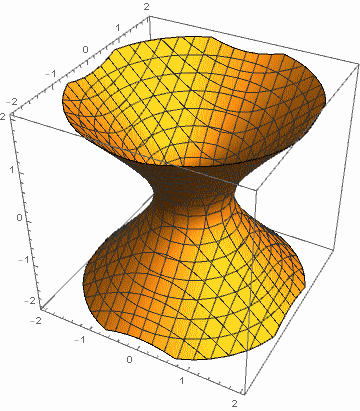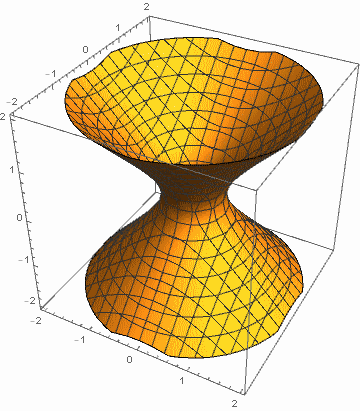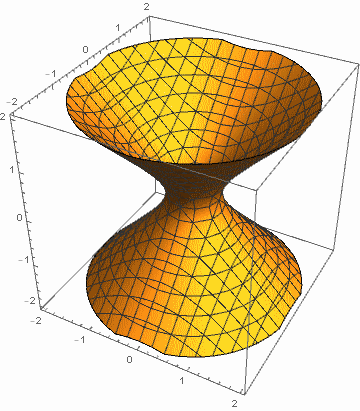
例2：令 a 在 1 和 4 之间变化，b, c 在 -1 和 -4 之间变化.

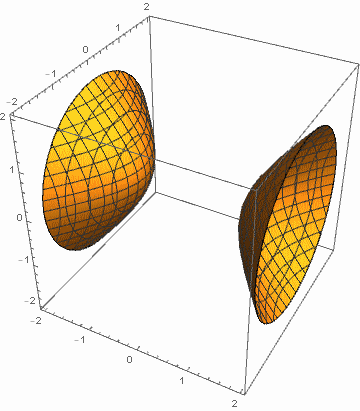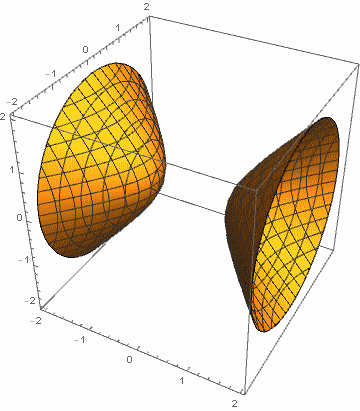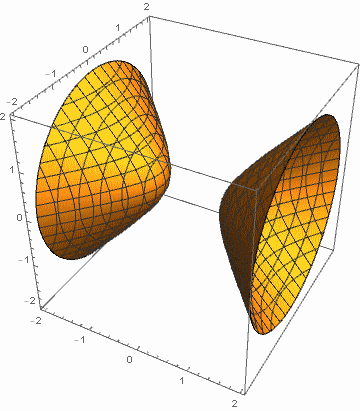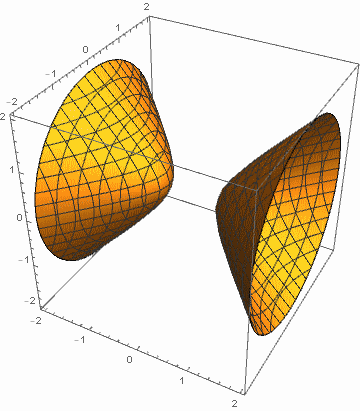
这启发我们，为搞清二次曲面有多少种类型，需且仅需对二次型的标准形进行伸缩，化成更“规范”的形式（比如将 a, b, c 化成 1 或 -1）.  这就引出了二次型的规范形概念.

课堂学习资料

课后学习任务

1. 利用所学的二次型知识探究一般二次曲面的分类（可参考图解）.

2. 实二次型的“惯性定理”跟“惯性”有关吗？确实是的，这是 Sylvester 研究刚体运动问题得到的结果. 刚体的惯性矩阵就是一个实对称阵，不同坐标系下得出的惯性矩阵是相互合同的.

3. 复习本章已学知识，并完成以下测验.