课程简介
下一节
引 言
实变函数论是一门什么样的课程,它研究的是什么样的问题,这是初学者首先想要知道的事情。
1902 年,法国数学家 Lebesgue 发表了题为《积分,长度与面积》的博士论文,利用以集合论为基础的"测度"概念建立了所谓的"Lebesgue 积分",从而形成了一个新的数学分支一实变函数论。因此实变函数论的核心内容是 Lebesgue 积分。
Lebesgue 积分是什么样的积分,它是怎么定义的,它与数学分析课程研究的 Riemann积分有什么不同。我们先回顾一下 Riemann 积分的定义。
定义 设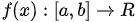 (实数集),
(实数集),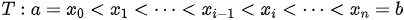 为区间
为区间 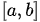 的一个分割。
的一个分割。 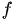 关于
关于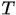 的 Riemann 和
的 Riemann 和 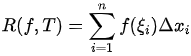 ,其中
,其中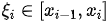 ,
,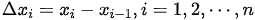 . 记
. 记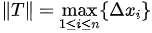 ,若存在常数
,若存在常数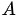 ,使对
,使对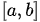 的任意分割
的任意分割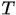 , 及任意的
, 及任意的 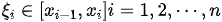 .有
.有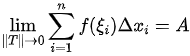 .则称
.则称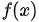 在
在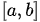 上 Riemann 可积,
上 Riemann 可积,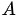 称为
称为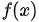 在
在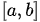 上的 Riemann 积分。记为
上的 Riemann 积分。记为


