ppt：

网课学习视频：

 第一章 潮汐与潮流

潮汐学：研究海洋、大气和地球潮汐现象的一门科学

与航海的关系：直接影响船舶航行计划的实施和航海安全

潮汐带来的影响：

1）载重量大的船舶，要等候潮水才能进出港口

2）航速，时间、燃料

本章学习目的：

1）从航海实际应用出发，阐明海洋潮汐的现象、成因

2） 利用《潮汐表》推算潮汐方法以及潮汐在航海中的应用。

第一节 潮汐的基本成因和潮汐术语

一、潮汐现象

海面在周期性外力作用下产生的周期性升降运动称为潮汐（tide），并将白天的海面上升称为潮，晚上的海面上升称为汐。海面上升的过程称为涨潮（rising tide 或flood tide），下降的过程称为落潮（falling tide 或 ebb tide），在一个涨落周期中，海面达到最高点时，称为高潮（high water，HW），达到最低点时，称为低潮（low water，LW）。伴随海面周期性的升降运动而产生的海水周期性的水平方向流动称为潮流（tidal stream）。

一个周期中的海面升降、即海水的涨落并不是均匀的，高潮过后，海面缓慢下降，降到高、低潮的中间时刻附近，下降得最快，然后又减慢，直到发生低潮为止。低潮前后的一段时间，海面处于停止状态，称为―停潮（stand tide），停潮的中间时刻称为―低潮时（time of low water，简记TLW）；高潮前后的一段时间，海面处于停止状态，称为―平潮（slack tide），平潮的中间时刻称为―高潮时（time of high water，简记THW）。

从低潮时到高潮时的时间间隔叫―涨潮时间（duration of rise ），从高潮时到低潮时的时间间隔叫―落潮时间（duration of fall ）。

二、潮汐的基本成因

潮汐是由天体的引潮力（tide-generating force）产生的。天体的引力与惯性离心力的合力称为引潮力。对潮汐影响大的是月球和太阳的引潮力，其中月球引潮力是产生潮汐的主要外力。即月球对地面海水的引力，以及地球绕地（球）、月（球）公共质心进行平动运动所产生的惯性离心力是形成潮汐的主要原动力。本节从航海实际需要出发，扼要地利用平衡潮理论(静力学理论)分析潮汐的基本成因，为方便讨论，提出两点假设：

（1）整个地球被等深的大洋所覆盖，所有自然地理因素对潮汐不起作用；

（2）海水质点间没有摩擦力和惯性力，外力使海水在任何时刻都处于平衡状态 。

1.月球的引力

在地球和月球的引力系统中，按万有引力定律，月球与地球之间的引力与地、月两球的质量成正比，与它们之间距离的平方成反比。若以mM 表示月球质量，mE 表示地球质量，R 表示地球与月球中心间的距离，则地球和月球之间的引力为：

式中：k 为万有引力系数。

设月球中心至地球上任一点的距离为r，则地球表面任意点处，单位质量的海水所受的月球引力为：

由此可见，对于地球上各点来说，其所受月球引力的大小和方向均不相同，即不同地点的水质点所受到的月球引力的大小，是随着该点与月球中心的距离r 的不同而不同的，离月球近的水质点受力大，离月球远的则受力小，引力的方向均指向月球中心。

2．惯性离心力

1）地、月系统的公共质心

由式看出，地、月之间具有相同的相互吸引力，但地、月系统能维系平衡，是由于它们绕着其共同质心运动的结果。由质心计算公式可计算出，地、月系统的公共质心（G）位于地、月中心（M）的连线上，距离地球中心（E）约0.73 倍的地球平均半径处。

2）地球上各点的惯性离心力

月球和地球都绕着它们的公共质心进行平动运动，周期为一个太阴月，约27.3 日。对于地球上的各点，它既受到月球引力，又受到绕公共质心运动产生的惯性离心力的作用。当只考虑地、月系统时，地球所受到的月球引力与地球绕公共质心的平动运动产生的惯性离心力近似平衡。就地球中心而言，单位质点的惯性离心力f E 与该质点的月球引力的大小相等、方向相反。即：

下面考察地球表面的水质点受到的月地平动运动所产生的惯性离心力。

图4-1-3 是地球绕公共质心一个周期的运动示意图。当地球中心在E１位置时，月球中心便在M１的方向上。同样地，随着月球和地球的相对运动，E2 与M2 对应，E3 与M3对应，E4 与M4 对应。总之，地球中心E 是以―月－地系统‖的公共质心G 为中心，以GE=0.73R 为半径作圆周运动。

当地心E 绕公共质心Ｇ作圆周运动时，由于地球自转周期与其绕公共质心的运动周期相比可以忽略，因而，在月地系统绕其公共质心的运动中，地球上任意两点的联线始终保持着平行运动。地球绕公共质心的运动状态类似于自行车踏脚板的运动，自行车踏脚板在被踩踏的过程中，踏脚板始终是平行运动的，即踏脚板上的任意平行线段在运动过程中始终保持着平行状态。同样地，当地球绕公共质心的运动中，地球中心E 以公共质心G为中心作运动时，地球表面上任意一点 A也在绕其自己的中心G保持与地心E同步运动。

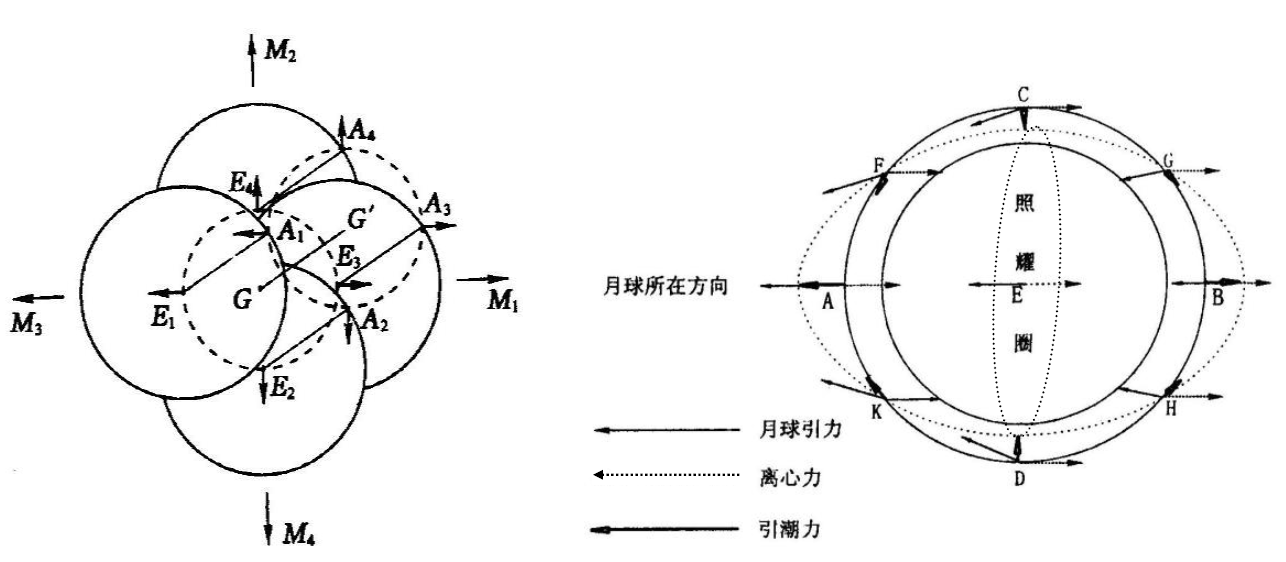
如图4-1-3 所示，A 是地球面上的任意一点，当地球中心绕G 运动一周时，对应地，A 也相应地由A1 运动到A2 、A3、A4，且始终保持E1A1//E2A2//E3A3//E4A4//GG，即地球上任意线段的空间方向始终保持不变。因此，地球表面上任意一点A 的圆周运动半径AG与地心E绕G 作圆周运动的半径EG 相同，且运动的角速度也相同。所以，A点所受到的惯性离心力必定与E 点的惯性离心力大小相等，方向相同，即相互平行。它们都背离自己的圆周运动中心，即背离月球方向。

3．月球引潮力及月潮椭圆体

1）月球引潮力

月球引潮力是月球引力和地球绕公共质心进行平动运动所产生的惯性离心力的合力，地球上的任意点均会受到引潮力的作用。 图4-1-4是地球上各点的月球引潮力的大小和方向示意图。在地球中心，引力与离心力大小相等，方向相反，处于力的平衡状态，引潮力等于零。在其它各点处，引力和离心力不会相互抵消，从而产生了它们的合力即引潮力。

2）月潮椭圆体与潮汐的形成 

月潮椭圆体是在假设地球表面全被等深海水所覆盖时，受月球引潮力的作用时海面达到新的平衡状态时形成的椭圆体，其长轴与月地连线一致（图4-1-4中的点线椭圆体）。

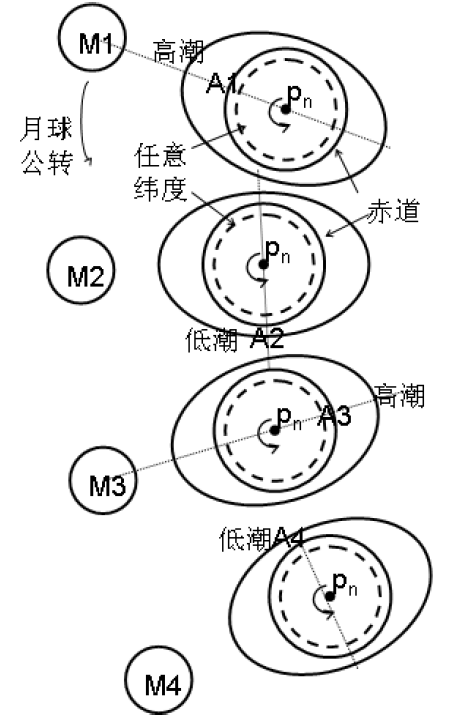
同一地点的潮汐是在引潮力和地球自转的共同作用下形成的。图4-1-5是假设月球赤纬等于零的月潮椭圆体，椭圆体的长轴位于月地连线上与地轴垂直。pn为地理北极，测者A位于任意纬度，A1、A2、A3、A4分别表示地球表面上任意一点A在地球相对于月球自转一周中的四个特殊位置。在地球自转中，当月球位于M1，A位于A1时，月球处于上中天，A处于月潮椭圆体的长轴上，该地的海面相对上升到最高位置，形成高潮；当地球自转时，月球在绕公共质心公转，当地球相对于月球自转过90°即月球公转到M2时A转到了A2，A处于月潮椭圆体的短轴，该地的海面相对下降到最低位置，产生低潮；当地球相对于月球转过180°，即月球公转到M3，A转到A3时，月球处于该地的下中天，A处于月潮椭圆体的长轴，海面又上升到最高位置，即发生了第二次高潮；同理，当A自转到A4时，该地的海面再次下降到最低，发生了第二次低潮。月球连续两次上（下）中天的间隔时间，称为一个太阴日，平均约为24h50min。由此可见，由于月球引潮力和地球自转的共同作用，使同一地点的海面发生周期性的升降现象，从而形成了潮汐。

人们对某地海平面连续观测发现，海面每天上升和下降的高度是不等的，涨落时间点也不一致。上述的理论仅解释了潮汐的基本成因，实际中的潮汐现象比较复杂，经总结有―三个不等和一个滞后现象。 

1. 潮汐的周日不等

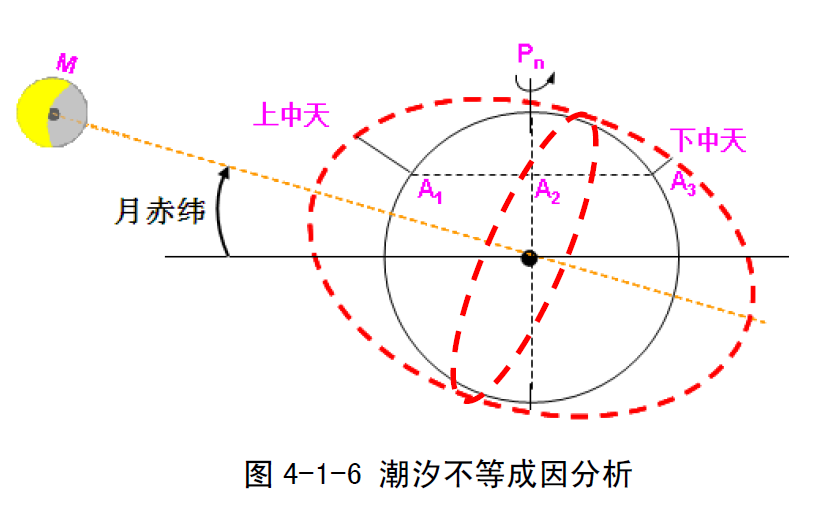
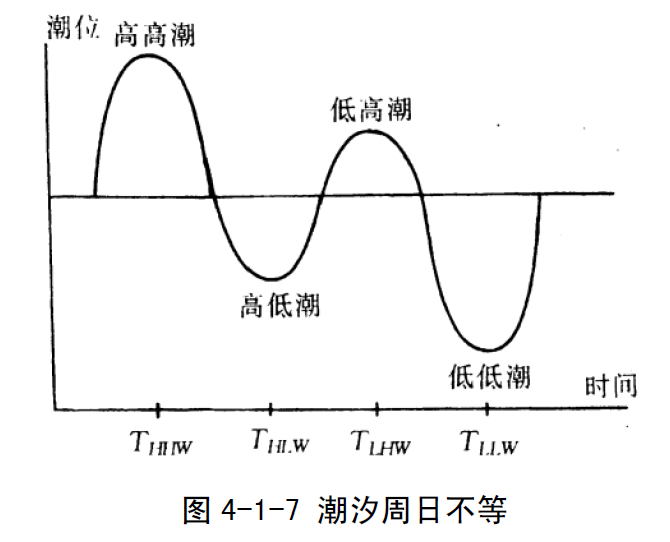
在同一太阴日中所发生的两次高潮或两次低潮的潮高以及相邻的高、低潮的时间间隔并不相等，这种现象称为潮汐周日不等（diurnal inequality of tide）。潮汐周日不等产生的主要原因是月赤纬不等于零以及测者的纬度不等于零所致。 图4-1-6是当月赤纬不等于零时的潮汐椭圆体，其长轴与赤道平面之间的夹角等于月球赤纬。类似于图4-1-5的分析，地球自转中当A转到A1和A2时，发生第一次高潮和低潮，转到A3 和A4 时，发生第二次高潮和低潮。显然，同一太阴日中的两次高潮（低潮）的高度不等，其中较高的一次高潮叫高高潮（higher high water，HHW），较低的一次高潮叫低高潮（lower high water，LHW），而两次低潮中较高的一次叫高低潮（higher low water，HLW），较低的一次叫低低潮（lower low water，LLW）。而且间隔时间A1A2不等于A2A3，即相邻的高、低潮（或低、高潮）之间的间隔时间（涨、落潮时间）也不等。

潮汐周日不等的显著程度随着月球赤纬的增大或测者纬度的升高而加剧。当月赤纬为0°时，由以上分析可知，在一个太阴日中产生两次高潮，两次低潮，两次高潮的高度几乎相等，两次低潮的高度也几乎相等，相邻的涨落潮时间各约为6h12min，这一现象称为半日潮。我们把月赤纬等于零时的潮汐称为赤道潮（equatorial tide）或分点潮。当测者纬度很高，月亮赤纬又较大时，一个太阴日中，相邻的低高潮和高低潮的高度可能相差无几，从而形成一天只有一次高潮、一次低潮，这一现象称为日潮。当月赤纬达到最大时，潮汐周日不等现象最为显著。月赤纬最大时的潮汐称为回归潮（tropical tide）。图4-1-7 是潮汐周日不等成因分析示意图。

2.潮汐的半月不等

人们连续数日对同一地方海面进行观测发现：月亮从朔（新月）望（满月）到两弦，又从两弦到朔望的位置改变，引起潮差（相邻的高、低潮潮高的差值）不断变化。即从新月到上弦，潮差逐渐变小，从上弦到满月则逐渐变大，从满月到下弦，从下弦到新月又产生同样的变化。这样以半个朔望月（约14.5 日）为周期的潮汐变化，称为潮汐的半月不等（semi menstrual inequality of tide）。

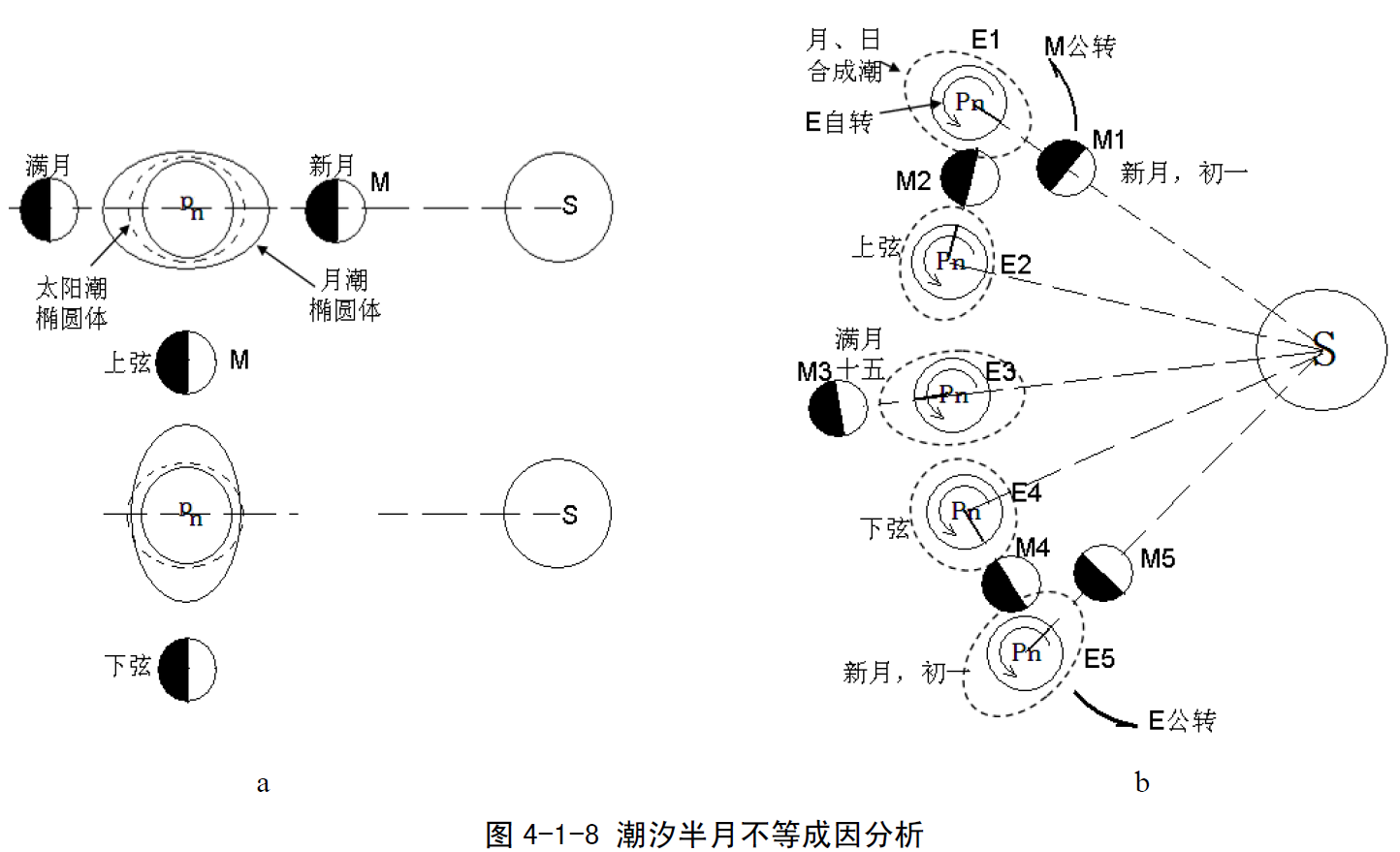
月亮引潮力和太阳引潮力的共同作用以及月亮和太阳的相对位置的变化产生了潮汐的半月不等。由于月球引潮力要比太阳引潮力约大2.17 倍，对于潮汐现象而言，主要与月球的引潮力有关。但太阳的引潮力同样会产生太阳潮汐椭圆体（图4-1-8a），且太阳两次上（下）中天的时间间隔为一个太阳日，即24h。当太阳的赤纬不等于零时，也会发生太阳潮汐的周日不等现象。因而，太阳潮的存在增加了潮汐现象的复杂性。由于月球、太阳和地球在空间周期性地改变着它们的相对位置（图4-1-8b），因而发生了潮汐半月不等现象。

图4-1-8a是月亮和太阳子午面一致时和垂直时的两潮汐椭圆体关系示意图。图4-1-8b是太阳、月球和地球运动及合成潮的变化示意图。地球E如图所示的绕太阳S公转，月球M绕地月公共质心公转，pnS为太阳子午面，pnM为月亮子午面。在一个朔望月中，地、月相对于太阳由E1、M1（阴历初一）运动到了E5、M5（阴历初一），潮汐便不断发生变化。当月、地处在M1、E1新月（初一，月相）或M3、E3满月（十五，月相○）时，太阳子午面和月亮子午面一致，它们的引潮力方向接近相同（图4-1-8a上图），相互加强，使合成的潮汐椭圆体的长轴更长，短轴更短，从而出现高潮相对最高，低潮相对最低，潮差最大，此时的潮汐称为大潮（spring tide）。而当月球处于M2、E2上弦（初七、八，月相）和M4、E4下弦（廿二、廿三，月相）时，太阳和月亮的子午面相互垂直，它们的引潮力方向接近相反（图4-1-8a下图），被相互抵消一部分，使合成的潮汐椭圆体的长轴变短、短轴变长，出现高潮相对最低，低潮相对最高，潮差相对最小，此时称为小潮（neap tide）。

3.潮汐的视差不等 

潮汐的视差不等（parallax inequality of tide）是由于月球和太阳与地球间的距离变化，使月球引潮力和太阳引潮力发生变化，从而产生的潮汐不等现象。月球在近地点时的引潮力要比其位于远地点时约大40%。由此产生的潮汐不等，称为月潮视差不等，因其周期为一个恒星月（约27.3日），故又称周月不等。同样，地球在近日点时的太阳引潮力比远日点时约大10%。由此产生的潮汐不等称太阳潮视差不等，因其周期为一年，故又称周年不等。

四、理论潮汐与实际潮汐的差异

1．复杂的实际潮汐

上述对潮汐成因、潮汐不等问题的讨论，都是根据牛顿的潮汐静力学理论，在理想的假设条件下进行的。事实上，海水有粘滞性，海洋深浅不一，海底崎岖不平，海水与地面有很大的摩擦力，因此，高潮并不发生在月上（下）中天之时，而是滞后一段时间才发生。从月上（下）中天时刻到当地出现第一次高潮的时间间隔称高潮间隙，到当地出现第一次低潮的时间间隔称低潮间隙；大潮也不发生在朔望日，而往往发生在朔望后的1～3 天。朔望日到发生大潮的间隔天数称为潮龄（tide age）。我国沿海，潮龄一般为2～3 天，即阴历初三、十八发生大潮。

沿岸海区地理条件较大洋更加复杂。其水深变化大，海底地形复杂，岸线曲折，尤其是浅滩和狭窄海湾的存在，不仅能改变海水涨落的差距，而且能改变潮汐性质。例如：我国的―钱塘怒潮‖，就是由于漏斗状河口，越往上游水深越浅，涌入的潮波形成相当大的落差，形成所谓怒潮或暴涨潮，潮水像一堵墙一样涌来，甚为壮观；加拿大东南芬地湾的海面落差最大可达18m；我国秦皇岛港的潮汐有别于渤海湾内的邻近港口；墨西哥湾中相距很近的两个地区出现性质完全不同的潮汐现象。

另外，潮汐还受大风、气压变化（如台风）、洪水、结冰等影响而增水或减水，尤其在浅水海湾或河口港，其影响可能非常显著，不可忽视。有些河口航道，由于河流下泄水的影响，落潮时间明显长于涨潮时间，落潮流速也明显大于涨潮流速。

2．调和常数

实际的潮汐现象是非常复杂的，为了实际应用，数学家们将复杂的潮汐看成是许多简谐振荡的合成。把每一简谐振荡视为由一个假想天体引起的潮汐，从而把十分复杂的不规则的潮汐振荡分解为很多正规的潮汐振荡。每种正规潮汐，即由一个假想天体引起的潮汐，称为分潮（tidal component）。每个分潮曲线又用两个参素描述：分潮振幅（tidal component amplitude），用H 表示；分潮迟角（tidal component epoch），即假想天体上中天到该分潮高潮的时间间隔，用g 表示。H 和g 称为调和常数（harmonic constants）。大部分假想天体引起的分潮振幅很小或周期很长，在实用上可忽略不计，在一般的预报潮汐中仅涉及11 个分潮。英版《潮汐表》（Admiralty Tide Tables）每卷在第三部分（part Ⅲ）中列出了当年各港4 个主要分潮的H 和g 的数值，以便用来大致计算任意时刻的潮汐。这四个主要分潮是： M2 主要月球半日分潮；S2 主要太阳半日分潮；K1 月球和太阳合成日分潮； O1 主要月球日分潮。

五、潮汐类型与潮汐术语

1．潮汐类型

潮汐的涨落现象是因时因地而异的，在中版《潮汐表》的附表中给出了各港口的潮

汐性质数据，其计算式为：

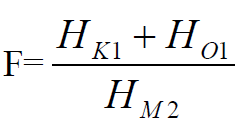
（H 为分潮的振幅），F 也叫潮型系数，其大小决定了港口的潮汐类型，分为以下几种：

1）半日潮港：每个太阴日都有两次高潮和两次低潮。两次高潮和两次低潮的高度都几乎相等，涨潮时间和落潮时间也接近相等，F＜0.5。我国大部分港口属于半日潮港口。

2）日潮港：在半个月中有连续1/2以上天数出现一个高潮，一个低潮日潮，而在其余日子则为半日潮，F＞4.0。我国南海有许多地点（北部湾、红岛、德顺港等）的潮汐，都属于日潮类型港口。

3）混合潮港：它界于半日潮与日潮之间。

（1）不正规半日潮混合潮港 对于具有半日潮特性，但在一个太阴日内其相邻的高潮（或低潮）的高度相差很大，涨潮时间和落潮时间也不等的港口又称为不正规半日潮港，0.5≤F＜2.0。 

（2）不正规日潮混合潮港 在半个月中，连续日潮的天数不超过7天，其余天数为不正规半日潮的港口又称为不正规日潮港，2.0≤F≤4.0。

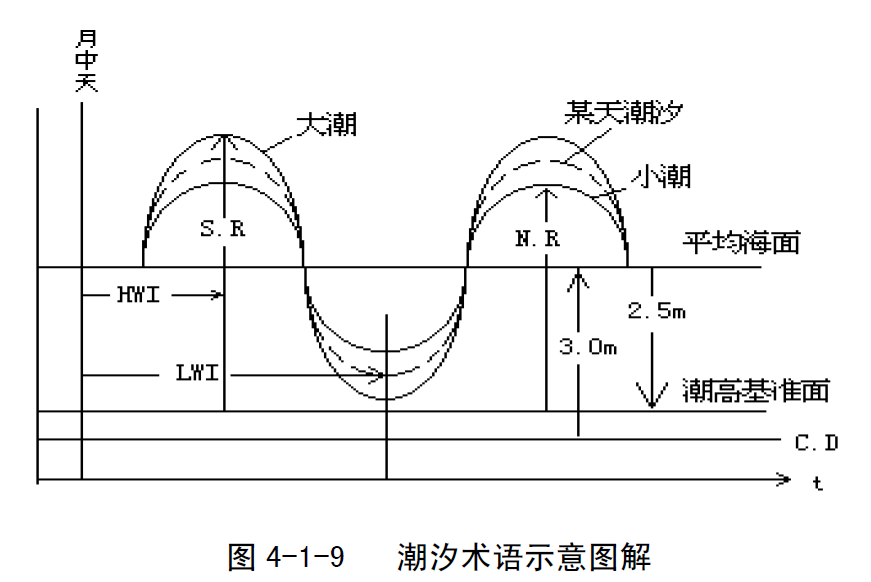
2．潮汐术语 在论述潮汐成因和潮汐不等等问题时已介绍了一些潮汐术语，为了掌握和运用潮汐计算方法，下面再介绍一些（图4-1-9）： 平均海面（mean sea level，MSL）：根据长期潮汐观测记录算得的海面平均高度。中版潮汐表中的平均海面由潮高基准面起算，即表中―潮高基准面‖的在平均海面下的数值。 潮高基准面（tidal datum，TD）：潮汐预报表中的潮高起算面，从平均海面向下度量。

海图深度基准面（chart datum，CD）：海图的水深起算面，从平均海面向下度量。CD一般与TD一致，当两者一致时，实际水深等于海图水深加上当时潮高。如果两者不一致，求实际水深时，应对两者的差值进行修正（见本章第二节中的―潮汐推算的应用‖）。

潮高（height of water）：从潮高基准面至某时刻潮面的高度。

高潮高（height of high water）：从潮高基准面至高潮面的高度，即高潮时的潮高。 低潮高（height of low water）：从潮高基准面至低潮面的高度，即低潮时的潮高。 潮差（range）：相邻的高潮高与低潮高之差。潮汐表中将大潮时的平均潮差称大潮差，小潮时的平均潮差称小潮差。

大潮升（spring rise，SR）：从潮高基准面到平均大潮高潮面的高度。 小潮升（neap rise，NR）：从潮高基准面到平均小潮高潮面的高度。 潮汐间隙：某地的月中天时刻到该地发生第一个高潮或者低潮的时间间隔。月中天时刻至发生第一个高潮的时间间隔为高潮间隙（high water interval，HWI）；至发生第一个低潮的时间间隔为低潮间隙（low water interval，LWI）。

平均高（低）潮间隙（mean high（low） water interval，MHWI（MLWI））：半个太阴月或其整数倍的每个高（低）潮间隙的平均值。 因我国的潮汐表采用专门方法计算潮汐间隙，所以，我国潮汐表中的平均高（低）潮间隙是用格林尼治月中天时刻计算的，即格林尼治月中天时刻加上高（低）潮间隙得到我国某港发生高（低）潮的时间。