一、思考与练习:
1.区分以下概念。
算术平均数和加权平均数;
众数与中位数;
离均差与方差;
2.表示集中趋势的量数主要有哪些?各在什么情况下使用?
3.表示离散趋势的量数主要有哪些?常使用哪一种?
4.标准化值的意义和用途是什么?
5.方差与标准差的关系是什么?
6.全距、标准差和方差的分数可以为负吗,为什么?
7.正态分布表中的Z、Y和P值分别代表什么意思,如何查正态分布表?
8.什么是3σ原则?
9.写出下列各项的代表符号:
a.样本平均数 b.总体平均数 c.样本标准差 d.总体标准差
e.原始分数 f.样本方差 g.总体方差
10.甲乙两班数学考试成绩的平均数和标准差分别为甲=80分,已=78,甲的标准差为6.3分,已的标准差为5.8分,试比较其离散程度。
11.如果S=0,分布中的分数如何?举例说明。
12.SPSS软件中的频数(Frequencies)命令、描述(Descriptive)命令和均值(Means)命令主要具有怎样的功能。
13.在一堂统计课上,教师进行了三项测试。每位学生的成绩都在原始成绩上有权重。测试一、测试二和测试三的权重分别是1、2和2。下面是一位学生的测试分数,求这个学生分数的总体平均数。
14.根据下列分布情况,判断是选择平均数还是中数表示集中趋势,并解释原因。
a.2,3,8,5,7,8
b.10,12,15,13,19,22
c.1.2,0.8,1.1,0.6,25
15. 已知下列各分布的集中趋势值,分别判断分布是正态、正偏态还是负偏态。
a. 平均数=14,中数=12,众数=10
b. 平均数=14,中数=16,众数=18
c. 平均数=14,中数=14,众数=14
16.计算下列各项的平均数,中数以及众数。
a.5,2,8,2,3,2,4,0,4
b.30,20,17,12,30,30,14,29
c.1.5,4.5,3.2,1.8,5.0,2.2
17.请求出下列分数的全距、标准差和方差.
a. 6,2,8,5,4,4,7
b.24,32,27,45,48
c.2.1,2.5,6.6,0.2,7.8,9.3
18.下面是一次生物考试的分数。
分数 | f | 分数 | f |
95-99 | 3 | 65-69 | 7 |
90-94 | 3 | 60-64 | 6 |
85-89 | 5 | 55-59 | 5 |
80-84 | 6 | 50-54 | 3 |
75-79 | 6 | 45-49 | 2 |
70-74 | 8 |
|
|
a.求中数 b.求众数
19.求下列样本分数的标准差,相对a来讲,为什么b的标准差如此之大呢?
a.6,8,7,3,6,4
b.6,8,7,3,6,35
20.初中一年级一班的期末数学成绩服从正态分布,平均分为105分,标准差为15分。请估计:
(1)该班成绩在120-150分的同学所占比例。
(2)该班80%的学生的成绩集中在哪个分数段内?
二、SPSS操作题。
21.使用SPSS计算以下数学考试成绩的平均数、标准差、方差和全距。
Mathexam:78,65,47,38,86,57,88,66,43,95,73,82,61
1. 2.已知某中学初中三年级1、2两个班学生的语文考试成绩分组如表所示。
按成绩分分组/分 | 1班学生人数/人 | 2班学生人数/人 |
60分以下 | 20 | 30 |
60-70 | 30 | 40 |
70-80 | 80 | 100 |
80-90 | 50 | 70 |
90以上 | 20 | 10 |
合计 | 200 | 250 |
(1)分别计算两个班学生的平均成绩。
(2)分别计算两个班学生成绩的标准差,比较两班学生平均成绩的代表性。
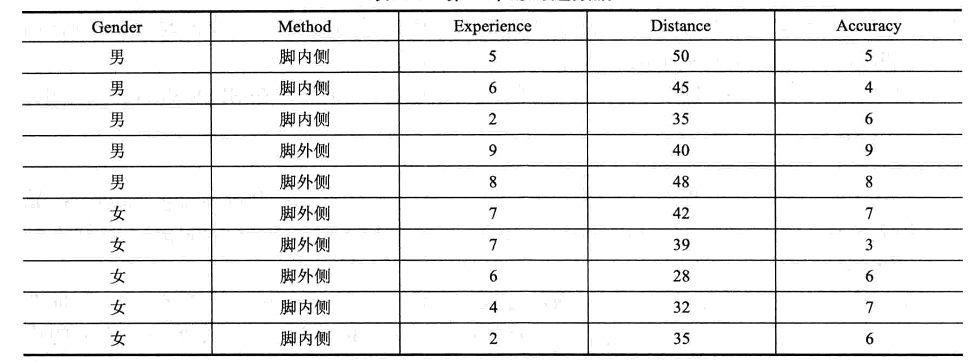
22.一位足球教练想评价一场足球比赛中两种不同踢法(脚内侧和脚外侧)的效果,5个男孩和5个女孩,使用其中一种方法踢球,记录了他们踢球的距离(英尺)和准确度(范围为1-10),也测量了小孩的经验水平(值越高表明经验越多)。下表给出了数据。(10分)
(1)在SPSS中将数据录入,写出主要步骤。
(2)分别报告性别和踢球方法不同分组的频数。
(3)报告全部样本的经验水平、踢球距离和准确度的均值和标准差,并生成标准分数。
(4)分别报告男孩和女孩的经验水平、踢球距离和准确度的均值和标准差。