教学视频

注意：本教学视频及内容仅供教学使用

本节主要内容

虚位移与虚功.广义坐标与自由度

1.虚位移与虚功

质点或质点系在给定瞬时不破坏约束而为约束所许可的任何微小位移，称为质点或质点系的虚位移。

虚位移可以是线位移，也可以是角位移。通常用变分符号表示虚位移。

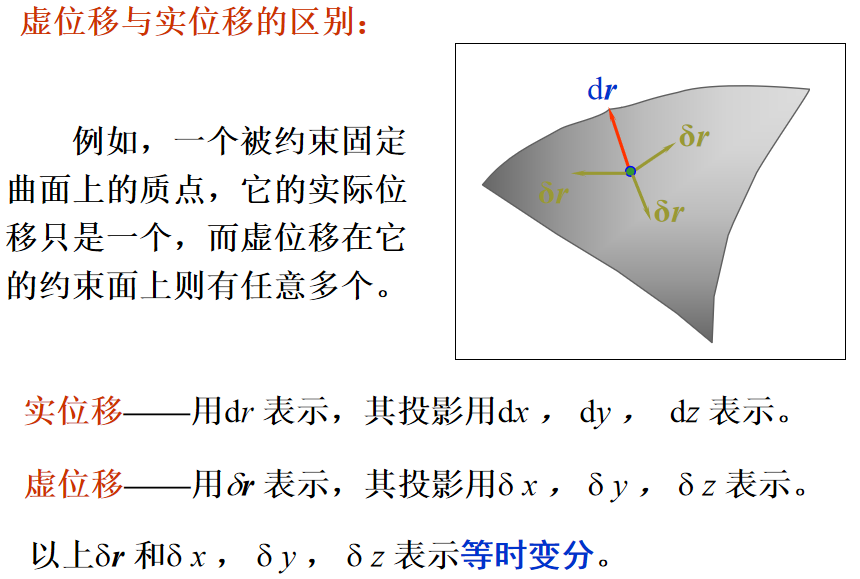
虚位移与实位移的区别：

与实际发生的微小位移（简称实位移）不同，虚位移是纯粹几何概念，是假想位移，只是用来反映约束在给定瞬时的性质。它与质点系是否实际发生运动无关，不涉及运动时间、主动力和运动初始条件。

虚位移仅与约束条件有关，在不破坏约束情况下，具有任意性。而实位移是在一定时间内真正实现的位移，具有确定的方向，它除了与约束条件有关外，还与时间、主动力以及运动的初始条件有关。

将矢径进行等时变分就是虚位移，将几何约束方程进行等时变分就可以得到虚位移之间的关系。

质点系中各质点的虚位移之间存在着一定的关系, 确定这些关系通常有两种方法：

几何法和解析法

2.广义坐标与自由度

确定一个受完整约束的质点系的位置所需的独立坐标的数目，称为该质点系的自由度的数目，简称为自由度。

用来确定质点系位置的独立参数，称为广义坐标。

拓展阅读

再论实位移与虚位移——从“无功约束”概念谈起  

略论变分原理之科学美