第三节 影响遗传平衡的因素
影响遗传平衡的因素主要包括:非随机婚配 (Nonrandom mating)、基因突变 (Gene mutation)、选择 (Selection)、遗传漂变 (Genetic drift)、基因流 (Gene flow)、减数驱动 (Meiotic drive)、以及遗传搭车 (Genetic draft)。
一、非随机婚配
随机婚配(Random mating)指随机选择婚配对象的婚配行为,这种选择不受表型、基因型、距离、经济条件等等各种因素的影响。非随机婚配主要包括选型婚配、分层婚配和近亲婚配。非随机婚配可能会降低群体杂合度,不改变基因频率。
近亲婚配 (Consanguineous mating) 指有血缘关系的个体间的婚配。近亲婚配增加了隐性基因纯合的机会,不利的隐性表型面临选择,最终将改变后代的等位基因频率。近亲的程度可用亲缘系数表示;近亲婚配使后代基因纯合的概率则用近婚系数表示。
(一)近婚系数
近婚系数(coefficient of inbreeding )是指个体的一对等位基因来自祖先的同一个等位基因的概率,通常用F表示。现在能够影响近婚系数的祖先只能是父母的共同祖先。近婚系数也可以针对婚配类型来说,个体的近婚系数与父母婚配类型的近婚系数一致。这里我们以姨表兄妹婚配的例子来说明近婚系数的计算,系谱图下:
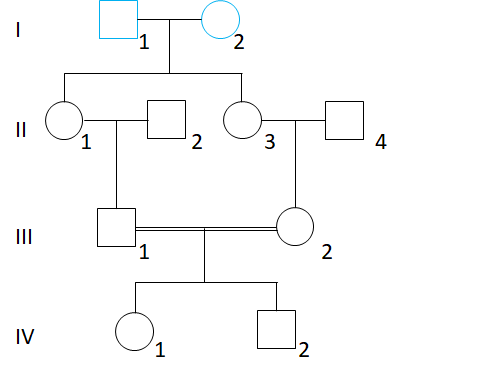
1. 常染色体遗传的近婚系数
这里要求IV1的近婚系数,则找到其父母的共同祖先I1和I2,假设他们的基因型分别为A1A2和A3A4。那么,IV1要的一对等位基因都来自祖先也就是说IV1的基因型有四种可能:A1A1、A2A2、A3A3、A4A4。
IV1基因型是A1A1的概率,也就是A1这个等位基因通过左右两边同时传下来的概率,分为如下几步:I1 → II1 → III1 → IV1、以及 I1 → II3 → III2 → IV1,这每一步传递的概率都只有1/2,A1从两边都成功从I1传到IV1的概率就是
[(1/2)×(1/2)×(1/2)]×[(1/2)×(1/2)×(1/2)] = (1/2)6
I1个体有两个等位基因,他对近婚系数的贡献就是2×(1/2)6,同I2个体的贡献也一样。因此IV1的近婚系数为:
F = 2×(1/2)6 + 2×(1/2)6 = 1/16
很容易就能看出,个体常染色体遗传的近婚系数为其父母亲缘系数的1/2。同样,很容易就算得,对于常染色体遗传,一级亲属婚配的近婚系数为1/4,二级亲属婚配的近婚系数是1/8,三级亲属婚配的近婚系数是1/16。
2. X连锁遗传的近婚系数
同样的例子,在X连锁遗传中,先找到共同祖先I1和I2,假设他们的基因型分别为X1Y和X2X3。那么,IV1要的一对等位基因都来自祖先也就是说IV1的基因型有三种可能:X1X1、X2X2、X3X3。不同的是,在考虑等位基因的传递的过程中,父传子和父传女的概率是不同与常染色体基因的,父传子的概率是0,而父传女的概率是1。因此,等位基因X1通过I1 → II1 → III1 → IV1及 I1 → II3 → III2 → IV1同时传到IV1的概率是
[(1)×(1/2)×(1)]×[(1)×(1/2)×(1/2)] = (1/2)3
而等位基因X2或X3通过I2 → II1 → III1 → IV1及 I2 → II3 → III2 → IV1同时传到IV1的概率是
[(1/2)×(1/2)×(1)]×[(1/2)×(1/2)×(1/2)] = (1/2)5
三个等位基因传递的贡献加起来就是IV1个体X连锁遗传的近婚系数:
F = 1×(1/2)3 + 2×(1/2)5 = 3/16
显然,对于X连锁遗传来说,不能简单通过亲属级别来说出近婚系数,而是需要画出系谱具体分析。而且,对于男性个体来说,不管其父母亲缘关系如何,其X连锁遗传的近婚系数肯定是0。
再看下边的两个例子:

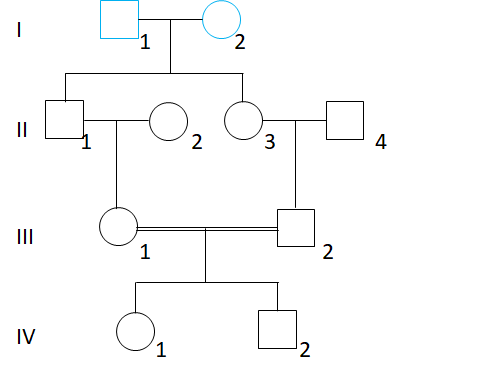
对于常染色体遗传,都是两条有5个个体的路径,近婚系数为= 1/16。对于X连锁遗传,左/上边的系谱所有路径都存在父传子(II2→III1),IV1的X连锁遗传的近婚系数为0,而对于右/下边的例子,IV1的X连锁遗传的近婚系数是 1/8。都是三级亲属婚配,X连锁近婚系数差异比较大,必须要具体问题具体分析。自己算算,看能否得到相同的结果。
在日常工作中可能会遇到比较复杂的情形,如果每次都写出每一步的概率,会比较麻烦,可以采用数个体的方法,详情见王老师网页。
(二)平均近婚系数
群体的平均近婚系数 (Average Inbreeding Coefficient)是所有个体的近婚系数的平均值。评价近亲婚配对群体的危害时,除近亲婚配率外,平均近婚系数也是重要的指标。平均近婚系数通常可通过统计婚配类型来估算,群体中第i种婚配类型的常染色体遗传近婚系数为Fi,共有Ni对,则群体平均近婚系数计算公式如下:
![]()
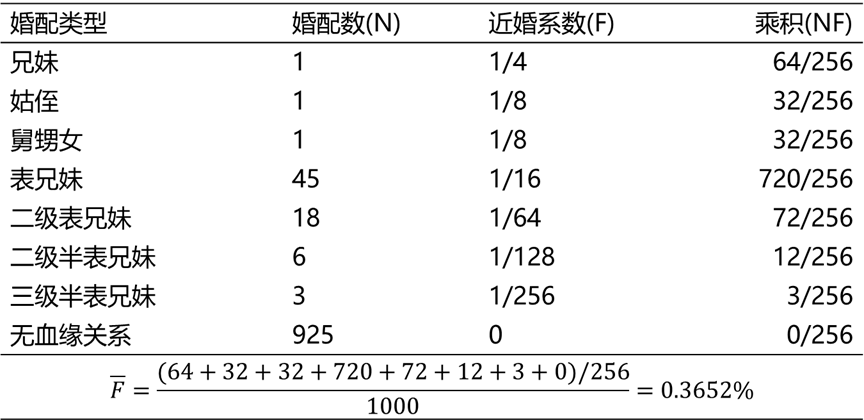
例题:在一次群体调查中发现,在1000例婚配,中兄妹婚配1例,姑侄婚配1例,舅甥女婚配1例,表兄妹婚配45例,二级表兄妹婚配18例,二级半表兄妹婚配6例,三级表兄妹户内3例,其余为非近亲婚配。这个群体的平均近婚系数是多少?
解:列表计算如下:
(三)近亲婚配对基因型频率的影响
基因型频率与近亲系数F、群体基因频率为p和q的关系如下:
![]()
![]()
![]()
显然,近亲婚配增加了隐性纯合子的频率。一代堂表兄妹姐弟婚配的子女的近婚系数为1/16,后代AR病发病风险为q2 +pq/16,与随机婚配比较,增加p/(16q)倍。显然,隐性遗传病越罕见(q越小),增加的倍数就越多。因此近亲婚配对群体有害。
二、选择
选择反应了环境因素对特定表型或基因型的作用,使个体的生活力和生育力改变。遗传学上用适合度来衡量生育力的大小,用选择系数来表示选择作用下适合度降低的程度。
(一)适合度
适合度(fitness)是在一定的环境条件下,某一基因型个体能够生存并将基因传给后代的几率,通常用w表示。适合度的大小用相对生育率表示。
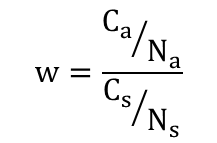
其中,Na个患者共生有Ca个小孩,这些患者的Ns个正常的同胞共有Cs个小孩
例题:丹麦一项调查发现:108名软骨发育不全性侏儒生育了27个孩子,这些侏儒的457个正常同胞共生育了582个孩子。侏儒患者的适合度(相对生育率,w)是多少?
解:将数据带入公式 w = (27/108)/(582/457) =0.2
(二)选择系数
选择系数(selection coefficient,s)指选择作用下,适合度降低的程度,通常s表示。即, s=1-w
三、突变
突变是正常基因和致病基因之间的相互转换,本质上是遗传物质的改变。A到a的突变率用μ表示,a到A的突变率用ν表示。群体中每代某一基因座位上基因突变的频率大约为10–5~10–7)。
突变会使群体中致病基因频率上升,而选择可淘汰掉部分致病基因。当群体平衡时, 突变增加的基因等于选择淘汰掉的基因。突变率的计算公式
AD:ν=sp (ν是a到A的突变率)
AR:μ=sq2 (μ是A到a的突变率)
XD:ν=sp (ν是a到A的突变率)
XR:μ=sq/3 (μ是A到a的突变率)
实际工作中,可通过群体发病率估算基因频率后结合选择系数计算突变率。
(一)显性致病基因突变率的计算(直接计算和用公式ν=sp计算)
例题:在100000个出生人口中有12人患同一种AD病,其中的两个患儿的父母一方有同种病, 其他10个患儿是由于基因新突变所致。求突变率。
解:通过新发病例可知:突变率=10/(100000×2)=1/20000
例题:94075婴儿中有10个为某AD病患者,求突变率ν。(该病s=0.80 )
解:发病率Ⅰ=10 /94075=1.063×10–4
发病率Ⅰ=p2+2pq≈2pq≈2p → p=(1/2)Ⅰ
μ=sp=s (1/2)Ⅰ=0.8×1/2×1.063×10–4=4.25×10–5
(二)AR致病基因突变率的计算(μ=sq2)
例题:苯丙酮尿症(AR)的发病率为6. 0×10–5。求致病基因突变率。(s=0.85)
解:发病率I =6. 0×10–5=q2
突变率µ=sq2=sⅠ=0.85×6. 0×10–5=5.1×10–5
(二)XR致病基因突变率的计算 [μ=(1/3)sq]
例题:甲型血友病(XR)男性发病率为8. 0×10–5。求致病基因突变率?(该病s=0.75)
解:已知男性发病率=8. 0×10–5=q
突变率 μ=(1/3)sq=1/3×0.75×8.0×10–5=2.0×10–5
四、遗传漂变
在小群体中可能出现后代的某基因频率较高,在一代代传递中基因频率明显改变,破坏了Hardy-Weinberg平衡。
遗传漂变的方向无法确定。究竟是那一种基因频率升高或下降,是一个随机事件。
五、基因流
随着群体迁移两个群体混合并相互婚配,新的等位基因进入另一群体,将导致基因频率改变,这种等位基因跨越种族或地界的渐近混合称之为基因流。
六、减数驱动
在减数分裂中,某个基因座位上特定的等位基因更多地被传递下去(即便这个等位基因本身可能是有害的),称为减数驱动。
七、遗传搭车
有利突变连锁的基因频率提高,称为遗传搭车。


