多元函数微分学是一元函数中极限、连续、可导和可微等知识点在多元函数中的推广。在学习基本概念的时候要注意与一元函数中相关的内容结合、对比。尤其要关注其中有差异的地方,如多元函数的可微、可导(偏导数存在) 、连续等基本概念之间的关系。除了基本的概念以外,本章的另一大重要内容是偏导数的计算:偏导数的四则运算法则、链式法则和隐函数存在定理都需要进行大量的练习，以熟练掌握。最后,对于多元函数的应用，要重点掌握多元函数极值(无条件、 条件）的定义和判别定理，尤其要区分无条件极值的必要条件和充分条件并注意它们各自适用的范围;对切线、法平面、切平面和法线则要熟悉它们的计算公式。

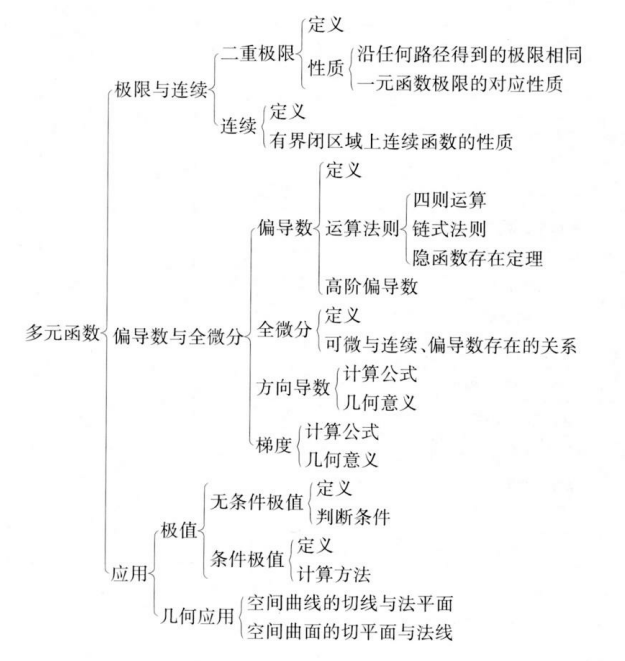
知识结构网