第三节 枚举与筛选
枚举:在解决问题时把所有可能的情况不重复、不遗漏、有顺序地一一列举出来。
筛选:在枚举过程中将重复的和不合要求的情况除去并将遗漏的情况找回来。
计数问题是小学数学中常常涉及的问题.
所谓计数,通俗地说就是数数,即把我们研究对象的个数数出来.
枚举法是解决关于计数问题的常用方法,枚举法就是把所要计数的对象一一列举出来,最后计算总数的方法.
对于简单的枚举法,一组既可列出;而对于较复杂的计数问题,难以用一组枚举法一一列举,就需要用“分组法”来计数了.其中列表和树状图都是应用枚举法解决问题常用的手段.
利用枚举法列举应注意:
①有序:即按一定的规律有顺序地进行计数;
②分组:即按照事物的相同属性(或不同属性)进行分组,分组的原则是既不重复又不遗漏;
③归纳:遇到复杂的问题,从符合条件的简单情形入手,利用不完全归纳法,分析归纳出一般的规律;
④对应:某些问题的种类与另一些问题有一一对应关系,可以利用它们之间的对应关系进行枚举法计数;
对应法:要求满足条件集合A的元素的个数,而又不易求出,常常寻找一个既能与集合A中的元素一一对应,同时又容易数出个数的集合B,从而由集合B的元素的个数推知集合A的元素的个数的方法叫做对应法.
⑤乘法原理与加法原理:
加法原理:如果要计数的对象有n类,每一类分别有m1种、m2种、m3种、…、mn种,那么这些对象总计有:m1+m2+m3+…+mn种,这种计数的方法叫做加法原理;
乘法原理:要完成一件事情需要n个步骤,完成每一个步骤各有m1种、m2种、m3种、…、mn种方法,那么完成这件事情共有:m1×m2×m3×…×mn种方法,这种计数的方法叫做乘法原理。
建议:先思考下列问题,再观看视频。
【例1】从2张5元、5张2元的纸币和10枚1元的硬币拿出10元钱来,有多少种不同的拿法?
【例2】窗台上有3盆花,分别是康乃馨、金盏花、百合花,把这3盆花摆成一排,有几种摆法?
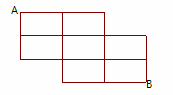
【例3】如图所示,从A点走到B点,沿线段走最短路线,共有多少种不同的走法?
【例4】将50这个数拆成10个质数的和,要求其中最大的质数尽可能的大,那么这个最大的质数是几?
(拓展阅读)请阅读下列链接内容:


