2020-03-10上传
（勘误：P18,页面中的sin(π/3)应该为sin(π/6)，感谢陈林同学的指正）
(注：视频中课件文字不够清晰，请结合上面的pdf文件观看)
视频1：平移变换与简单的旋转变换
（视频1已发现的BUG：1、如果手机播放没有声音，请带上耳机；或者请在电脑上观看；2、"tranform"应为“transform”,感谢段韬同学的指正）
视频2：旋转变换、齐次变换（2020-03-08）35分57秒
视频3：方向的其它表示方法
（视频3已发现BUG：1分25秒处，应为gamma弧度（误读成了gamma度））
视频4：基于Eigen3的坐标变换编程
示例程序：transform_tut.cpp
（向量点乘、叉乘、矩阵乘法、转置、逆矩阵、坐标系、坐标表示、变换、齐次变换矩阵求逆）
电子科技大学中山学院2020春季课程
第二周直播（部分对应 第二周答疑.pdf）2020-3-19
1、坐标系
ROS采用右手坐标系，如图1所示。由于本课程主要基于ROS介绍移动机器人自主导航，所以按照ROS的惯例采用右手坐标系。
在右手坐标系中，食指指向x轴的正方向，中指指向y轴的正方向，拇指指向z轴的正方向。
绕某个坐标轴的旋转方向根据如图2所示的右手法则定义：如果让右手的拇指沿某一坐标轴的正方向，那么其它四个手指旋绕的方向为旋转的正方向。
例如，对于移动机器人而言，x轴正方向指向机器人前进的方向，y轴的正方向指向（前进方向的）左边，z轴的正方向指向上方。围绕z轴的正方向的旋转是逆时针的。
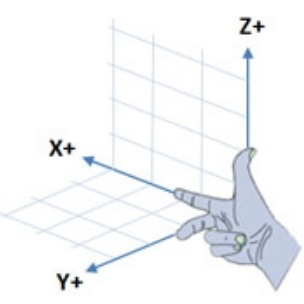
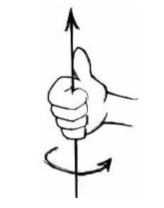
图1 右手坐标系 图2 右手法则
2、坐标与位姿
坐标给出某一点在坐标系中的位置，位姿包含位置和方向（机器人的朝向）。参照ROS的惯例，位置和长度的单位采用米(m)，时间采用秒(s)，线速度采用(m/s),角度采用弧度(rad)，角速度采用(rad/s)。
位姿(pose)：位姿包含位置(position)和方向(orientation)（如机器人或某个部件的朝向）。
位置：通过坐标表示。
方向：通过旋转矩阵、四元数等方式表示（将在后面介绍）
坐标：在三维空间中，坐标利用一个3x1的列向量表示。坐标总是相对于某个坐标系，当存在多个坐标系时，我们通过在点的左上角书写坐标系的名称来表示，如图3。
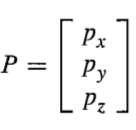
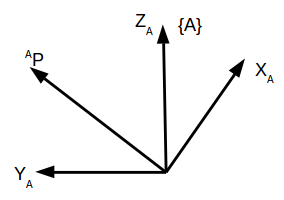
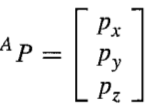
图3 坐标及其表示
3、坐标变换
平移变换：
平移(Translation)：设某点P在坐标系{B}中的坐标表示为BP。坐标系{B}与坐标系{A}具有相同的方向，即{B}相对于{A}只有平移，其平移变换通过向量表示，
是{B}的原点
在坐标系A中的坐标。
平移变换可以通过向量的加法实现，如图4所示,=
+
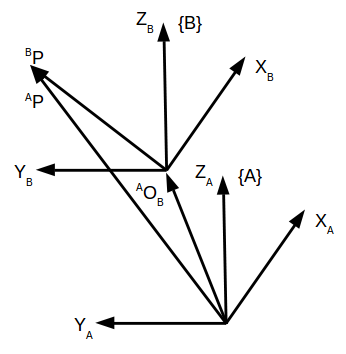
图4 平移变换
旋转(Rotation)：可以通过旋转矩阵ARB来表示坐标系{B}相对于坐标系{A}的方向。
图5显示的坐标系{B}是这样获得的：最初{B}与{A}重合，然后{B}绕{A}的Z轴旋转π/6。
旋转的右手法则：如果让右手的拇指沿某一坐标轴的正方向，那么其它四个手指旋绕的方向为旋转的正方向。
旋转矩阵ARB表示坐标系B相对与坐标系A的旋转。
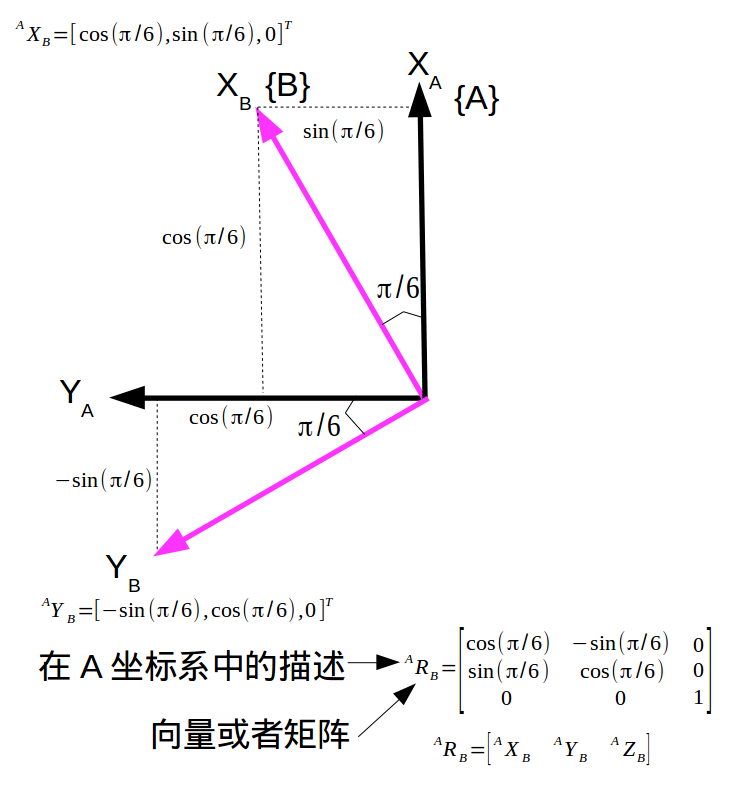
图5 旋转矩阵示例
该例显示：旋转矩阵ARB 的列向量是坐标系B的X, Y, Z 坐标轴的单位向量在坐标系A中的表示，这一结论将在后面予以证明。
可以看出，该矩阵的第一个列向量（cos(π/6) sin(π/6) 0)TT正是B坐标系在X方向单位向量在A中的表示。
在获得坐标系B相对于坐标系A的旋转矩阵之后，可以通过以下公式将坐标系B中某一点的坐标变换到坐标系A中。
Ap=ARB *Bp
例如：设Bp=（1 0 0)T
Ap=ARB *Bp=（cos(π/6) sin(π/6) 0)T
设坐标系{B}与坐标系{A}的原点相同，如图6，某点P在坐标系{A}中可以表示为：
P=(XA YA ZA)AP,其中XA，YA ，ZA分别为坐标系{A}的X,Y,Z轴的单位向量
P在坐标系{B}中可以表示为：
P=(XB YB ZB)BP,因此：
(XA YA ZA)AP= (XB YB ZB)BP
(XA YA ZA)T(XA YA ZA)AP=(XA YA ZA)T (XB YB ZB)BP，注意到(XA YA ZA)T(XA YA ZA)为单位矩阵，因而有
Ap=ARB Bp
其中：
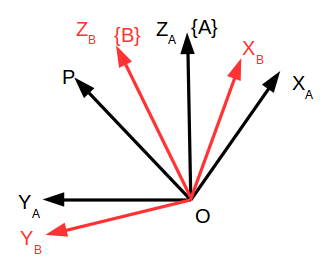
图6 旋转矩阵
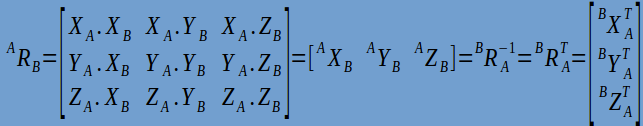
旋转矩阵有以下特点：
旋转矩阵是正交矩阵（Orthogonal Matrix）（就是说:其逆矩阵为其转置矩阵）
其行列式的值为1
每个列向量（及行向量）都是单位向量
三个列向量相互正交
三个行向量相互正交
坐标变换：若坐标系{B}相对与坐标系{A}既有旋转又有平移，可以引入坐标系{B'},{B'}的原点与{B}的原点重合，{B'}的方向与{A}的方向一致。
有：B'P=B'RBBP, AP=B'P+AOB'
由于OB'=OB，且 B'RB=ARB，所以
坐标变换可以通过以下公式实现：
AP=ARBBP+AOB
注意到AP和BP是同一个点P在坐标系{A}和{B}的坐标(并不是两个不同的点，只是一个点在不同坐标系下的描述)
齐次变换(homogeneous transform):为了把包含旋转和平移两类变换表示成矩阵形式，通常采用4X4的变换矩阵ATB，同时把3X1坐标扩展为4X1的向量：
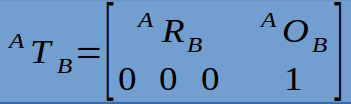
这样，变换可以表示为：
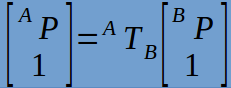
变换运算(transformation operators)：齐次变换不仅可以用于计算同一个点在不同坐标系中的坐标，还可以作为一个运算，此时，同一坐标系下的点P1经过齐次变换T后，产生一个新的点P2：
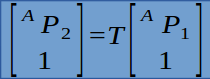
总结：齐次变换矩阵有三个作用：（1）可以表示坐标系之间的相对位姿，（2）用于坐标变换，（3）作为一种运算符
齐次变换给出了一种紧凑的书写方法，把旋转和平移变换用统一的矩阵形式表示，可以很好地表示多个坐标系之间的变换关系。但在实际的计算中，还是会采用旋转加平移的方法（以减少多余的乘以0的计算）。
参考：
[1]https://github.com/cse481sp17/cse481c/wiki/Lab-14%3A-Odometry-and-rotations
[3]《计算机视觉:一种现代方法(中文版)》,Computer Vision: A Modern Approach. David A. Forsyth, Jean Ponce 著. 林学訚，王宏译
[4]《视觉SLAM十四讲》从理论到实践，高翔、张涛著
[5]Introduction to Robotics:Mechanics and control. Third Edition. John J. Craig (Chapter 2 Spatial descriptions and transformations(p41-)
[6]Graphics Gems IV. Edited by Paul S. Heckbert. III.5 Euler Angle Conversion(p222-)
[7]http://eigen.tuxfamily.org/dox/group__TutorialGeometry.html
![[2]https://cloud.githubusercontent.com/assets/1175286/25162364/f754fce2-2476-11e7-9b78-8c7699c3a22c.png](https://cloud.githubusercontent.com/assets/1175286/25162364/f754fce2-2476-11e7-9b78-8c7699c3a22c.png){kind=link}