-
1.1前 言
-
1.2第1章 C语言程序设计基础知识
-
1.2.11.1 计算机基础知识概述
-
1.2.1.11.1.1 计算机与信息社会
-
1.2.1.21.1.2 计算机中信息的表示
-
1.2.1.31.1.3 计算机系统的组成
-
1.2.21.2 软件开发过程
-
1.2.2.11.2.1 计算机求解问题的步骤
-
1.2.2.21.2.2 算法的表示
-
1.2.31.3 C语言概述
-
1.2.3.11.3.1 C语言简史及特点
-
1.2.3.21.3.2 基本程序结构
-
1.2.3.31.3.3 基本语法单位
-
1.2.41.4 C语言程序的编写和运行
-
1.2.4.11.4.1 C程序的编写和运行步骤
-
1.2.4.21.4.2 Visual C++6.0介绍
-
1.2.51.5 案例研究
-
1.2.61.6 常见的编程错误
-
1.2.7小 结 一
-
1.2.8习 题 一
-
1.3第2章 基本数据类型及运算
-
1.3.12.1 基本数据类型
-
1.3.1.12.1.1 整型
-
1.3.1.22.1.2 浮点型
-
1.3.1.32.1.3 字符型
-
1.3.22.2 常 量
-
1.3.2.12.2.1 整型常量
-
1.3.2.22.2.2 浮点型常量
-
1.3.2.32.2.3 字符型常量
-
1.3.2.42.2.4 字符串常量
-
1.3.2.52.2.5 符号常量
-
1.3.32.3 变 量
-
1.3.3.12.3.1 变量的定义
-
1.3.3.22.3.2 变量的初始化
-
1.3.3.32.3.3 变量地址
-
1.3.42.4 运算符与表达式
-
1.3.4.12.4.1 算术运算符和算术表达式
-
1.3.4.22.4.2 赋值运算符和赋值表达式
-
1.3.4.32.4.3 关系运算符和关系表达式
-
1.3.4.42.4.4 逻辑运算符和逻辑表达式
-
1.3.4.52.4.5 位运算符和位表达式
-
1.3.4.62.4.6 条件运算符和条件表达式
-
1.3.4.72.4.7 逗号运算符和逗号表达式
-
1.3.4.82.4.8 其他运算符
-
1.3.52.5 混合运算与类型转换
-
1.3.5.12.5.1 自动类型转换
-
1.3.5.22.5.2 强制类型转换
-
1.3.5.32.5.3 赋值运算中的类型转换
-
1.3.62.6 运算的优先级与结合性
-
1.3.6.12.6.1 运算符汇总
-
1.3.6.22.6.2 运算符嵌套
-
1.3.6.32.6.3 表达式的运算顺序
-
1.3.72.7 数据的输入输出
-
1.3.7.12.7.1 字符输出函数putchar()和格式输出函数printf()
-
1.3.7.22.7.2 字符输入函数getchar()和格式输入函数scanf()
-
1.3.82.8 案例研究
-
1.3.9小 结 二
-
1.3.10习 题 二
-
1.4第3章 控制语句
-
1.4.13.1 程序的三种基本结构
-
1.4.23.2 复合语句
-
1.4.33.3 if条件分支语句
-
1.4.3.13.3.1 if流程
-
1.4.3.23.3.2 if else流程
-
1.4.3.33.3.3 else if流程
-
1.4.3.43.3.4 if语句嵌套
-
1.4.43.4 switch多路开关语句
-
1.4.53.5 for循环语句
-
1.4.63.6 while语句和do while语句
-
1.4.6.13.6.1 while语句
-
1.4.6.23.6.2 do while语句
-
1.4.73.7 循环嵌套
-
1.4.83.8 break,continue和goto语句
-
1.4.8.13.8.1 break语句
-
1.4.8.23.8.2 continue 语句
-
1.4.8.33.8.3 goto 语句
-
1.4.93.9 案例研究
-
1.4.10小 结 三
-
1.4.11习 题 三
-
1.5第4章 数组和结构
-
1.5.14.1 一维数组
-
1.5.1.14.1.1 一维数组的定义
-
1.5.1.24.1.2 一维数组元素的引用
-
1.5.1.34.1.3 一维数组的初始化
-
1.5.1.44.1.4 一维数组程序举例
-
1.5.24.2 二维数组
-
1.5.2.14.2.1 二维数组的定义
-
1.5.2.24.2.2 二维数组元素的引用
-
1.5.2.34.2.3 二维数组的初始化
-
1.5.34.3 字符数组
-
1.5.3.14.3.1 字符数组的定义和初始化
-
1.5.3.24.3.2 字符数组的输入输出
-
1.5.3.34.3.3 与字符串处理有关的几个函数
-
1.5.3.44.3.4 字符串应用举例
-
1.5.44.4 结构及结构变量的定义与访问
-
1.5.4.14.4.1 结构及结构变量的定义
-
1.5.4.24.4.2 结构成员的访问
-
1.5.4.34.4.3 结构变量的初始化
-
1.5.54.5 结构数组
-
1.5.64.6 程序举例
-
1.5.74.7 案例研究
-
1.5.8小 结 四
-
1.5.9习 题 四
-
1.6第5章 指 针
-
1.6.15.1 指针的概念和定义
-
1.6.1.15.1.1 指针的概念
-
1.6.1.25.1.2 指针的定义
-
1.6.1.35.1.3 指针的赋值
-
1.6.25.2 指针运算
-
1.6.35.3 指针和数组
-
1.6.3.15.3.1 指针与一维数组
-
1.6.3.25.3.2 指针与结构数组
-
1.6.45.4 字符串指针
-
1.6.4.15.4.1 指向字符数组的指针
-
1.6.4.25.4.2 指向字符串常量的指针
-
1.6.55.5 指针数组
-
1.6.65.6 指向指针的指针
-
1.6.75.7 程序举例
-
1.6.85.8 案例研究
-
1.6.9小 结 五
-
1.6.10习 题 五
-
1.7第6章 函 数
-
1.7.16.1 函数定义和调用
-
1.7.1.16.1.1 函数定义
-
1.7.1.26.1.2 函数调用
-
1.7.26.2 函数参数传递
-
1.7.2.16.2.1 传值调用
-
1.7.2.26.2.2 传址调用
-
1.7.36.3 函数与数组
-
1.7.3.16.3.1 数组元素作函数实参
-
1.7.3.26.3.2 数组名作为函数参数
-
1.7.46.4 函数与指针
-
1.7.4.16.4.1 返回指针的函数
-
1.7.4.26.4.2 指向函数的指针
-
1.7.56.5 函数与结构
-
1.7.5.16.5.1 结构指针及结构变量的传址调用
-
1.7.5.26.5.2 结构型函数
-
1.7.5.36.5.3 结构指针型函数
-
1.7.66.6 递归函数
-
1.7.76.7 命令行参数
-
1.7.86.8 标准库函数
-
1.7.96.9 程序举例
-
1.7.106.10 案例研究
-
1.7.11小 结 六
-
1.7.12习 题 六
-
1.8第7章 变量的存储类型
-
1.8.17.1 C程序的结构
-
1.8.1.17.1.1 C程序的组成
-
1.8.1.27.1.2 变量的作用域
-
1.8.1.37.1.3 变量的存储类型
-
1.8.27.2 内部变量
-
1.8.37.3 外部变量
-
1.8.3.17.3.1 在同一个源程序文件中使用外部变量
-
1.8.3.27.3.2 在不同源程序文件中使用外部变量
-
1.8.47.4 静态变量
-
1.8.4.17.4.1 静态局部变量
-
1.8.4.27.4.2 静态全局变量
-
1.8.57.5 寄存器变量
-
1.8.67.6 变量的初始化
-
1.8.77.7 动态内存分配函数
-
1.8.87.8 预处理功能
-
1.8.8.17.8.1 宏替换——#define
-
1.8.8.27.8.2 包含文件——#include
-
1.8.8.37.8.3 条件编译——#if、#ifdef、#ifndef
-
1.8.97.9 程序举例
-
1.8.10小 结 七
-
1.8.11习 题 七
-
1.9第8章 位域、联合、枚举和定义类型
-
1.9.18.1 位域及结构嵌套
-
1.9.1.18.1.1 位域
-
1.9.1.28.1.2 结构嵌套
-
1.9.28.2 联 合
-
1.9.38.3 枚 举
-
1.9.48.4 定义类型——typedef
-
1.9.5小 结 八
-
1.9.6习 题 八
-
1.10第9章 输入、输出及文件管理
-
1.10.19.1 流和文件
-
1.10.29.2 控制台I/O
-
1.10.2.19.2.1 字符输入输出——getchar()、putchar()
-
1.10.2.29.2.2 字符串输入输出——gets、puts
-
1.10.39.3 文 件
-
1.10.3.19.3.1 打开文件函数——fopen
-
1.10.3.29.3.2 关闭文件函数——fclose
-
1.10.3.39.3.3 标准流式文件stdin、stdout和stderr
-
1.10.49.4 用于文件的输入输出函数
-
1.10.4.19.4.1 单字符输入输出——getc()、putc()
-
1.10.4.29.4.2 行输入输出——fgets()、fputs()
-
1.10.4.39.4.3 数据块的输入输出——fread()、fw rite()
-
1.10.4.49.4.4 流式文件数据的格式化输入输出——fprintf()、fscanf()
-
1.10.4.59.4.5 文件的随机访问——fseek()
-
1.10.59.5 程序举例
-
1.10.69.6 案例研究
-
1.10.7小 结 九
-
1.10.8习 题 九
-
1.11第10章 C高级程序应用
-
1.11.110.1 链 表
-
1.11.1.110.1.1 引用自身的结构
-
1.11.1.210.1.2 单向链表
-
1.11.1.310.1.3 双向链表
-
1.11.1.410.1.4 循环链表
-
1.11.1.510.1.5 链表应用程序举例
-
1.11.210.2 与系统有关的库函数
-
1.11.2.110.2.1 BIOS接口调用函数
-
1.11.2.210.2.2 DOS系统调用函数
-
1.11.2.310.2.3 案例研究
-
1.11.310.3 声音程序
-
1.11.3.110.3.1 声音函数
-
1.11.3.210.3.2 音乐
-
1.11.3.310.3.3 应用举例
-
1.11.410.4 案例研究
-
1.12附 录
-
1.12.1附录A C语言的关键字
-
1.12.2附录B 运算符的优先级与结合性(见表B-1)
-
1.12.3附录C 常用字符ASCII表(见表C-1)
-
1.12.4附录D C语言中常用库函数
-
1.13参考文献
1
C语言程序设计
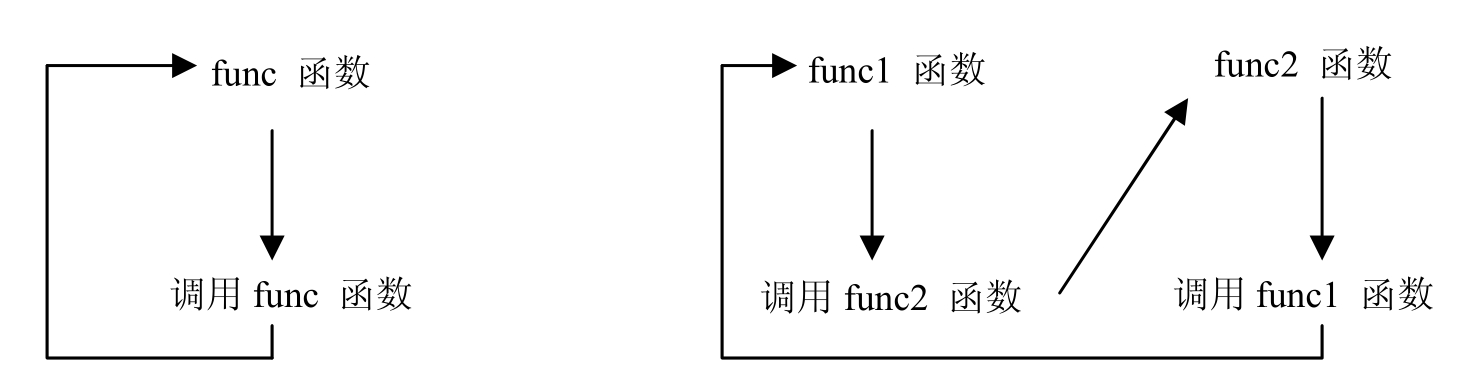
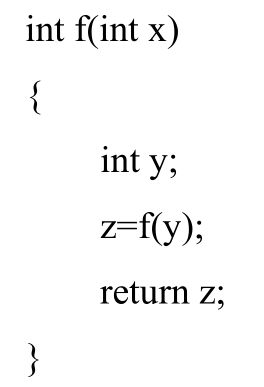


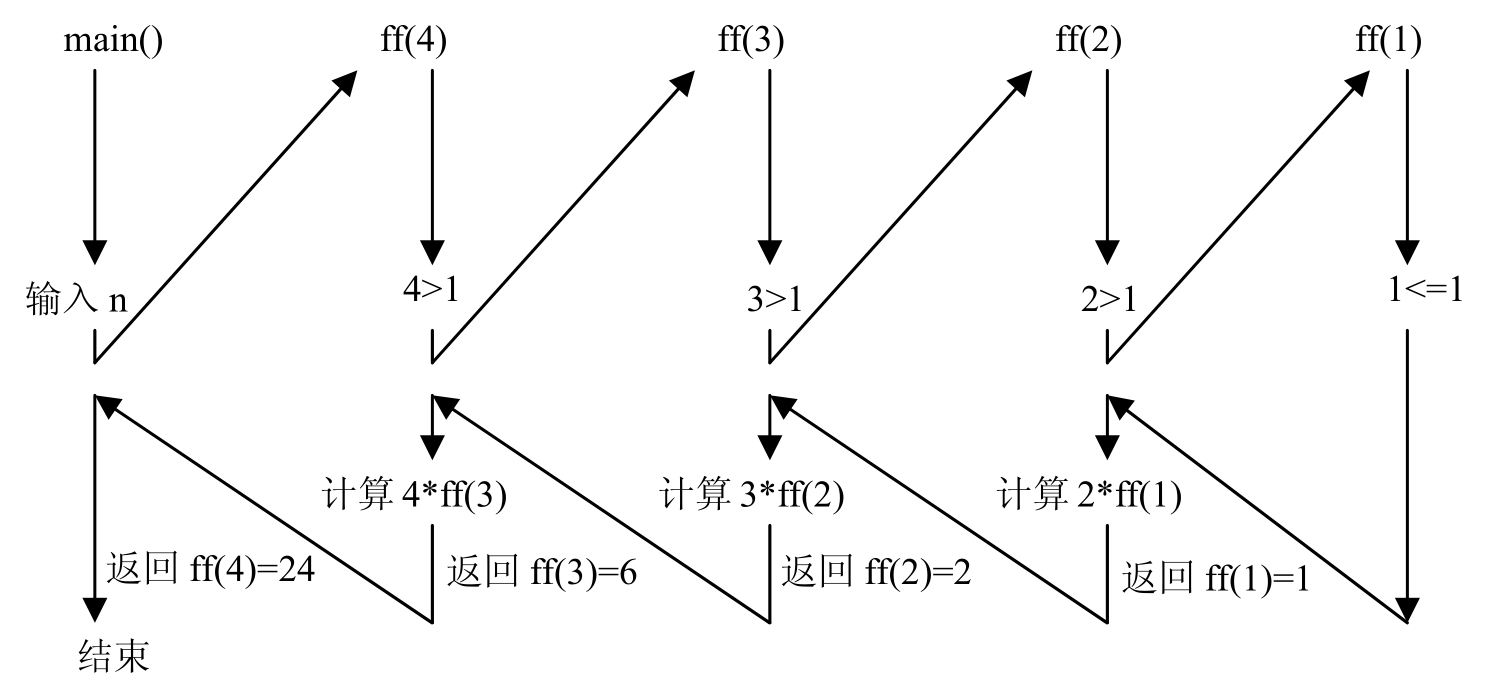
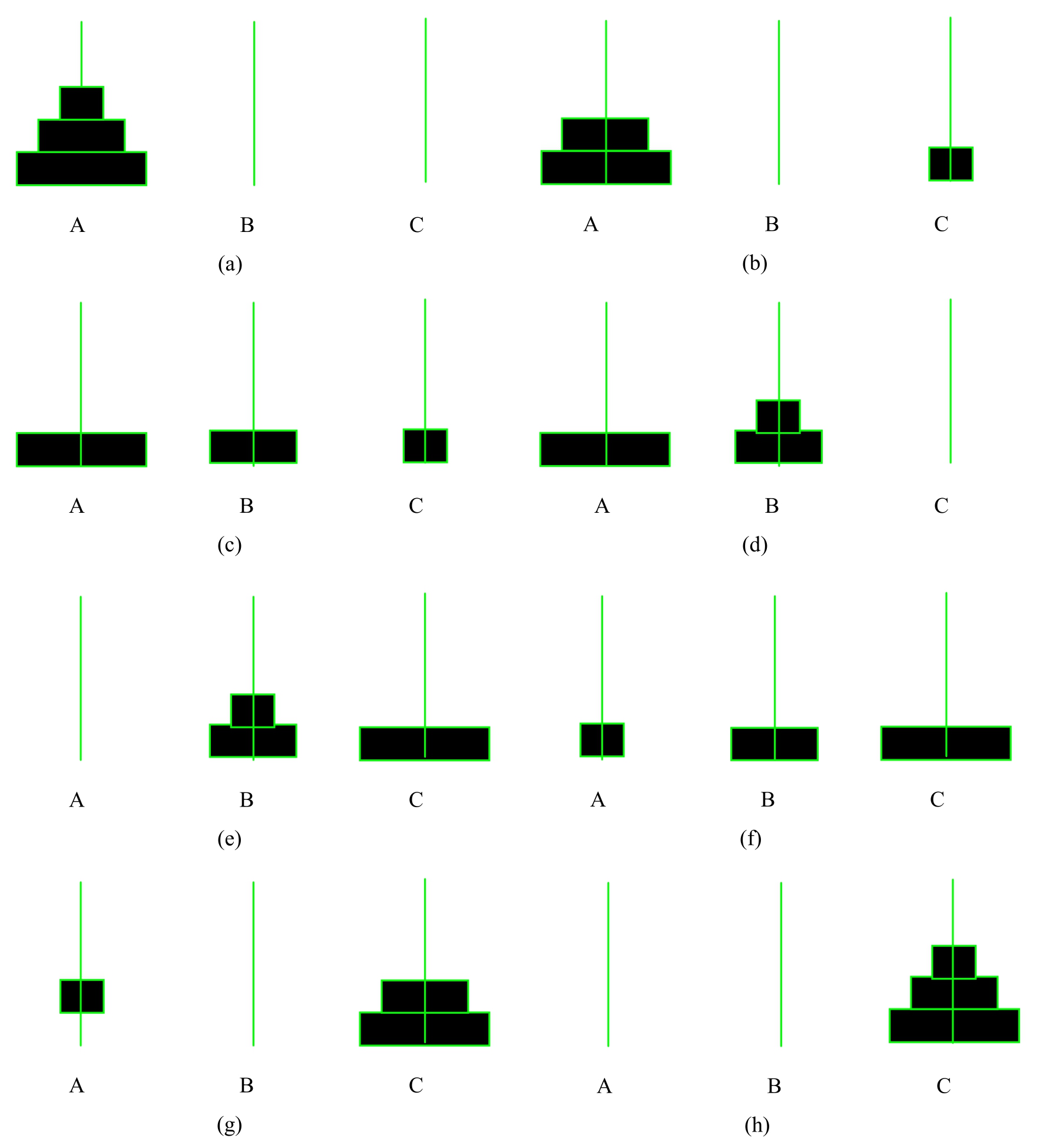


 省略基本情况,或者将递归步骤写得不正确,以致于不能归结到基本情况,引起无限“递归”,最终耗尽内存。
省略基本情况,或者将递归步骤写得不正确,以致于不能归结到基本情况,引起无限“递归”,最终耗尽内存。 如果一个非递归函数不经意地直接或间接调用了自身,会产生逻辑错误。
如果一个非递归函数不经意地直接或间接调用了自身,会产生逻辑错误。 避免导致指数级调用“爆炸”的递归程序。
避免导致指数级调用“爆炸”的递归程序。