8.7交流电路的功率

一、电路的功率

瞬时功率：电压瞬时值u和电流瞬时值i的乘积称为瞬时功率。用p表示

p =u i

1．电阻元件上的功率

（1）波形图法讨论：① 作u、i的波形图；② 作出p的波形图

（2）函数法讨论：设u= U_Rm sinωt，则

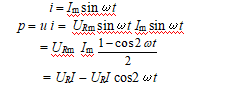
（3）平均功率（有功功率）：瞬时功率在一个周期内的平均值。用P表示。单位：W(瓦)、kW(千瓦)。

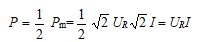
通常所说电器消耗的功率都是指有功功率。

（4）结论：P > 0，电阻元件是耗能元件；P= IU_R（W），有功功率（平均功率）。

2．纯电容电路的功率

（1）波形图法讨论：① 作u、i的波形图；②作出p的波形图

（2）函数法讨论：设u= U_Cmsinωt，则

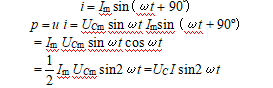
（3）结论：p = 0，说明电容元件不消耗功率，它是储能元件。无功功率：瞬时功率的最大值。用Q_C表示。单位：var（乏）、kvar（千乏）。

Q_C= U_C I

3．纯电感电路的功率

（1）波形图法讨论：①作u、i的波形图；②作出p的波形图。

（2）函数法讨论：设i= I_m sinωt，则

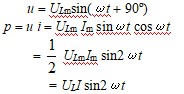
（3）结论：p = 0，说明电感线圈不消耗功率，它是储能元件。Q_L= U_LI（var），无功功率。

4．RLC串联电路的功率

（1）P= U_RI = UcosjI = U Icos j（2）Q= Q_L- Q_C=（U_L–U_C）I = U I sinj

（3）视在功率：总电压有效值与电流有效值的乘积称为视在功率。

S = UI，单位：V×A（伏安）、kV×A（千伏安）

（4）讨论：当cosj  = 1时，则电路消耗的功率与视在功率相等。

当cosj¹1时，则电路消耗的功率总小于视在功率；

当cosj = 0时，则电路的有功功率等于零，这时电路与纯电感、纯电容电路相同。

（5）功率三角形

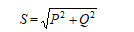
公式：P = UI cosj；Q = UI sinj；S= UI 适用于任何交流电路。

j——电路总电压和总电流的相位差。

电路的有功功率表示电路中所消耗的功率，电路的视在功率表示电源所能提供的功率。

二、功率因数

1．定义：电路的有功功率与视在功率的比值。它表示电能的利用率。

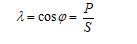
2．提高功率因数的意义

（1）功率因数越大，则说明电源能量的利用率越高。

例1：例1

（2）在同一电压下，输送一定的功率，则功率因数越高，线路中的电流越小，因而线路上的损耗也越小。

例2：例2

3．提高功率因数的方法

（1）在感性负载两端并联一只电容量适当的电容器可提高整个电路的功率因数。

（2）作出矢量图加以说明

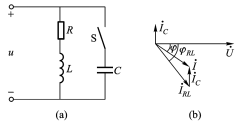
例3：在RLC串联电路中，已知电流为5A，电阻为30 W，感抗为40 W，容抗为80 W。求：（1）电路的阻抗；（2）该电路为什么性质电路？（3）电阻上的平均功率、无功功率；（4）电感上的平均功率、无功功率；（5）电容上的平均功率、无功功率；（6）电路的平均功率、无功功率和视在功率。