第5-6课时
2.1 定量分析的误差及减免方法
无论是化学分析法还是仪器分析法,在对实际样品的测量过程中,经常会出现下面的情况:即使由技术水平很高的某个人对同一样品用同一方法进行多次测量,结果也不会完全一样,那么这是为什么呢?
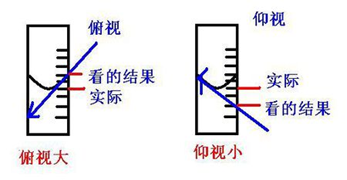
上面情况说明,在实际测量过程中,由于人、仪器、环境、方法设计等因素的影响,所得任何测量结果都不可能绝对准确,这表明分析过程中误差是客观存在的。
任何测量数据,客观上都存在误差,即误差是不可避免和消除的。定量分析也不例外,定量分析通常包括采样、称量、分解、分离、测定及计算等多个分析步骤,而每一步骤都会产生误差,故即使是采用最可靠的方法,使用最精密的测量仪器,由技术很熟练的操作人员在相同的条件下对同一试样进行多次测定,也不可能获得完全一致的分析结果。
那么,什么是误差呢?误差就是测量结果与真实值的差异。
误差 = 测量值-真实值,真实值也叫做真值。
虽然误差不可避免,但是可以采取措施减小误差,为此需要了解分析过程中产生误差的原因,并对所得数据进行归纳和取舍,判断它的准确性和可靠程度,使最终测量结果尽量接近真实值。
因此,在进行定量分析时,人们必须合理安排实验,对分析结果进行评价,判断分析结果的可靠程度,检查误差产生的原因并采取相应措施把误差降到最小,使分析结果准确可靠。
一、误差的分类
定量分析中,根据误差的来源和性质不同,可将误差分为系统误差和随机误差两大类。根据误差的性质和产生原因,可将其分为系统误差、偶然误差和过失误差三类。
1.系统误差
系统误差又称可测误差,它是由测定过程中某些经常性的、固定因素所造成的比较恒定的误差。它常使测定结果偏高或偏低,在同一测定条件下的重复测定中,误差的大小及正负可重复出现并可以测量。它主要影响分析结果的准确度,对精密度影响不大,而且通过适当方法校正以减小或消除。系统误差产生的主要原因有以下几种。
(1)方法误差
由于分析方法本身不够完善所造成,即使操作再仔细也无法克服。例如,重量分析中沉淀的溶解损失或吸附某些杂质而产生的误差;在滴定分析中,反应不完全、干扰离子的影响、滴定终点与化学计量点不同、副反应的存在等所产生的误差。它系统地影响测定结果,使之偏高或偏低。
(2)仪器误差
由于仪器本身不准确或未经校准引入的误差。例如天平两臂不等长,砝码腐蚀和量器刻度不准确等造成的误差。
(3)试剂误差
由试剂不纯或所用的蒸馏水含有微量杂质等因素所造成。
(4)主观误差
是指在正常情况下,操作人员的主观原因所造成的误差。如个人的习惯和偏向所引起的,如滴定管读数偏高或偏低;终点颜色辨别偏深或偏浅;平行测定时,主观上追求平行测定的一致性等引起的操作误差。
2. 偶然误差
偶然误差又称随机误差,它是由某些偶然因素所引起的误差,往往大小不等、正负不定。在正常情况下,平行测定结果不一致,甚至相差较大,这些都是属于随机误差。
例如测定时外界条件(如温度、湿度、气压等)微小变化引起的误差。这类误差在测定中无法完全避免,也难找到确定的原因,它不仅影响分析结果的准确度,而且明显地影响分析结果的精密度。
这类误差虽然不能完全消除,但其出现具有一定的规律性,表现为正态分布规律:正误差和负误差出现的概率相等,呈对称形式;小误差出现的概率大,大误差出现的概率小,很大的误差出现的概率极小。该规律可用正态分布曲线表示,如图3-1所示。图中横轴为以总体标准偏差σ 为单位的偏差,纵轴为误差出现的概率密度。

由此分布规律可知,随着测定次数的增加,随机误差的算术平均值逐渐趋于零。因此测定结果的准确度随测定次数的增加而提高。当测定次数较少时,分析结果的随机误差随测定次数的增加迅速减小,当测定次数大于10次时,随机误差减小将不明显,因此平行测定3~5次至多10次即可。
3. 过失误差
过失误差又称粗差,是由于操作人员工作中的过失,如粗心或不遵守操作规程等引起的误差,如容器不洁净、加错试剂、看错砝码、丢损试液、记录错误、计算错误等。过失误差严重影响分析结果的准确性,所测数据应弃去不用。
二、准确度与精密度
1.误差与准确度
一个物理量本身客观存在一个真实数量值,称为该物理量的真值。严格来说,任何物质中各组分的真实含量是不可测量的,但常将以下值当作真值处理。
① 理论真值:如某化合物的理论组成等。
② 计量学约定值:如国际计量大会上确定的长度、质量、物质的量单位等。
③ 相对真值:使用最精密的仪器,经过不同实验室、不同人员进行平行分析,用数理统计方法对分析结果进行处理,确定出各种组分相对准确的含量。此值也称标准值,一般用此值代表该物质中各组分的真实含量。
分析结果的准确度是指测定值与真实值相接近的程度。准确度的高低用误差来衡量。
误差表示测定结果与真实值的差异。差值越小,误差就越小,即准确度就高。
误差可用绝对误差和相对误差来表示。
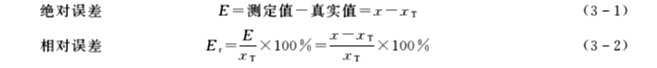
实际工作中,通常用多次平行测定结果的算术平均值x示测定结果,所以上述公式又可表示为
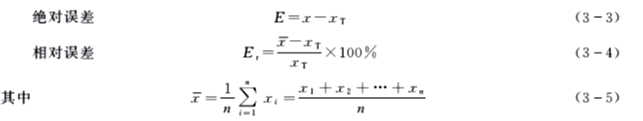
2.偏差与精密度
实际工作中,真值是无法知道的。虽然在分析化学中存在着“约定”的一些真值,如原子量等。但待测样品是不存在真值的,既然如此,用误差就无法衡量分析结果的好坏。在实际工作中,人们总是在相同条件下对同一试样进行多次平行测定,得到多个测定数据,取其算术平均值作为最后的分析结果。
精密度是指在相同条件下,用同样的方法,对同一试样进行多次平行测定时所得数值之间相互接近的程度。精密度的高低常用偏差来衡量。
偏差是指个别测定值与测定平均值之间的差值,它也分为绝对偏差和相对偏差。
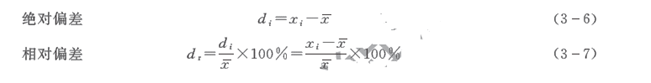
在实际工作中,常用平均偏差和相对平均偏差表示分析结果的精密度。
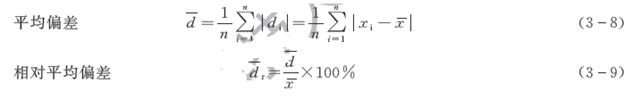
用数理统计方法处理数据时,常用标准偏差(又称均方根偏差)来衡量测定结果的精密度。
当测定次数n 趋于无穷大时,总体标准偏差σ表达如下:
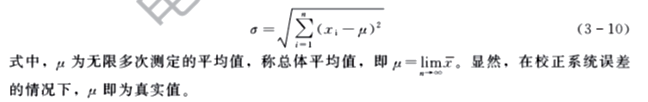
3.准确度与精密度的关系
从前面的讨论可知,系统误差是误差的主要来源,它主要影响分析结果的准确度。偶然误差主要影响分析结果的精密度。但实际工作中真实值往往是未知的,常常用测定平均值来代表真实值来计算误差的大小。通常在测定中精密度高的准确度不一定好,而准确度好必须以精密度高为前提。
图3-2表示甲、乙、丙、丁四人分析同一试样中铁含量的结果。由图可见:甲所得结果准确度与精密度均好,结果可靠;乙的精密度虽很高,但准确度较低,存在较大的系统误差;丙的精密度与准确度均很差;丁的平均值虽也接近于真值,但几个数值彼此相差甚远,仅是由于正负误差相互抵消才使结果接近真实值。如只取2次或3次平均,结果会与真实值相差很大,这个结果不可靠。
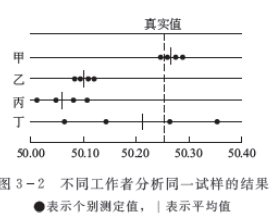
由此可得:①精密度是保证准确度的先决条件。精密度差,结果不可靠,也就失去了衡量准确度的前提。②精密度高准确度不一定好。只有在消除了系统误差的情况下,才能得到精密度高,准确度也好的测量结果。
4.提高结果准确度的方法
(1)选择合适的分析方法
化学分析法(重量法和滴定分析法)测定的准确度高(千分之几),但灵敏度低,适用于常量(>1%)组分的分析。
仪器分析法测定的灵敏度高,但准确度较低,适用于微量(0.01%~1%)或痕量(<0.01%)组分的分析。
在实际工作中,需要根据试样的具体情况和对准确度的要求以及客观实际条件等综合考虑,选择合适的测定方法。
(2)减少测量的相对误差
为了保证分析结果的准确度,必须尽量减小测量误差。例如,一般分析天平(电子天平)称量两次的误差为±0.0002g,为了使测量时的相对误差在0.1%以下,试样质量就不能太小。相对误差的计算公式如下:

可见称取试样的质量必须在0.2g以上。
在滴定分析中,滴定管读数两次的误差常有±0.02mL,为了使测量时的相对误差小于0.1%,消耗滴定剂的体积必须在20mL以上。
而在光度分析法中,控制取样量,即显色溶液的浓度使吸光度A 落在0.15~1.0范围内,测量的相对误差较小。
(3)检查和消除系统误差
系统误差是造成测定平均值偏离真实值的主要原因,因此检查并消除系统误差是至关重要的。
A、对照试验
在相同条件下,用含量准确已知的标准试样与待测试样同时进行测定,通过对标准试样的分析结果与其标准值的比较,可以判断测定是否存在系统误差。或者用其他可靠的分析方法与所采用的分析方法进行对照,以检验是否存在系统误差。对照试验是检查系统误差的最有效方法。
B、回收试验
在测定试样某组分含量χ1的基础上,加入已知量的该组分χs,再次测定该组分含量χ2。由下式计算加标回收率:

回收率越接近100%,系统误差越小。回收试验常用于微量组分或复杂样品的分析,如果微量组分的平均回收率达95%~105%,则可以认为分析结果可靠。
C、空白试验
由蒸馏水、试剂和器皿带进杂质所造成的系统误差,一般可通过做空白试验来扣除。所谓空白试验,就是在不加待测组分的情况下,按照待测组分分析同样的操作步骤和条件进行实验。实验所得结果称为空白值。从试样分析结果中扣除空白值后,就得到比较可靠的分析结果。当空白值较大时,应找出原因,加以消除。如选用纯度更高的试剂和改用其他适当的器皿等。在进行微量分析时,空白试验是必不可少的。
D、方法校正
用公认的标准方法进行对照试验,找出校正数据以消除方法误差。
E、仪器校正
在实验前,应根据测定误差要求,对测量仪器,如砝码、滴定管、移液管、容量瓶等进行校正,以减小这些仪器引起的系统误差。
(4)减少偶然误差
随机误差是由偶然的不固定的原因造成的,在分析过程中始终存在,是不可消除的。在消除系统误差的前提下,平行测定次数越多,平均值越接近真实值。因此,增加测定次数,可以提高平均值精密度,使平均值更接近真实值。在一般化学分析中,对于同一试样,通常要求平行测定3~5次。如对测定结果的准确度要求较高时,可增加测定次数至10次左右。
教学实验(探索性等实验例外)采用的是较为成熟的分析方法,可认为不存在方法误差;若实验采用符合纯度要求的试剂和蒸馏水,可认为不存在试剂误差;若仪器的各项指标也调试到符合实验要求,可认为无仪器误差。那么实验结果误差的来源就是随机误差。若出现非常可疑的离群值,基本可判断实验存在着操作者的操作误差或过失。
(5)避免过失误差
过失误差减免的方法是在学习过程中必须养成严格遵守操作规程、耐心细致地进行实验的良好习惯,培养实事求是、严肃认真、一丝不苟的科学态度。


