★掌握四个量子数的取值及其物理意义，量子数组合和轨道数的关系；原子轨道、电子云的角度分布；基态原子核外电子排布遵守的三条规律（Pauli不相容原理，能量最低原理，Hund规则）；

★熟悉原子轨道和概率密度的概念；原子轨道的角度分布图、径向分布函数图的意义和特征；熟悉电子组态与元素周期表的关系，有效核电荷、原子半径及电负性变化规律；

★了解氢原子的Bohr模型；电子的波粒二象性，测不准原理；电子云的径向分布；元素性质的周期性变化规律；元素和人体健康。

1803年英国科学家道尔顿提出了著名的原子学说：一切物质都是由分子组成的，分子是保持原有物质一切化学性质的最小颗粒；各种分子又是由更小的粒子—原子组成的；

1897年，英国物理学家汤姆逊发现了电子，并确认电子是原子的组成部分；(“枣糕模型”：原子是一个平均分布着正电荷的粒子，其中镶嵌着许多带负电的电子) 

1911年，英国物理学家卢瑟福提出了行星原子轨道模型；        

1913年，年轻的丹麦物理学家玻尔在卢瑟福原子结构模型的基础上，建立了玻尔原子结构模型，成功解释了氢光谱，推动了原子结构理论的发展。

1911年 英国物理学家Rutherford E根据α粒子散射实验，提出了 原子的有核模型（nuclear model），即“行星系式”原子模型 ：原子核好比是太阳，电子好比是绕太阳运动的行星，电子绕核高速运动。 

Rutherford E的模型存在一个解决不了的问题:电子在核外空间有怎样的状态?根据他的模型，绕核运动的电子会连续地辐射电磁波，得到连续光谱,并且因电磁辐射而损失能量的电子会堕入原子核内。但事实是原子光谱是线性光谱，原子是稳定的。

解决这一矛盾的是丹麦科学家Bohr N，他借助Plank关于热辐射的量子理论，应用于原子中电子的运动，建立了氢原子模型。

人们用眼睛能观察到的可见光的波长范围是400—760 nm。当一束白光通过石英棱镜时，不同波长的光由于折射率不同，形成红、橙、黄、绿、青、蓝、紫等没有明显分界线的彩色带状光谱，这种带状光谱称为连续光谱。

                                 连续光谱

气态原子被火花、电弧或其他方法激发产生的光，经棱镜分光后，得到不连续、有明显分界的线状光谱，这种线状光谱称为原子光谱。

 

                        

                            氢原子光谱及实验示意图

Bohr在1913年提出Bohr假定：

1、能级假说  

 核外电子在一定的轨道上运动，在这些轨道上运动的电子不放出能量也不吸收能量，电子处于某种“定态”（stationarystate）。轨道上电子有特定的能量值，称为“能级”（energy level)。核外电子能量为

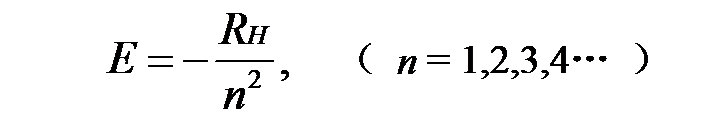
式中RH是常量 ，值为2.18×J，n称为主量子数,取整数值。n=1时能量最低，称为原子的基态，其它能量较高的状态都称为激发态。

2、能级间的跃迁

当电子的能量由一个能级改变到另一个能级，称为跃迁。电子跃迁所吸收或辐射光子的能量等于电子跃迁后的能级( E )与跃迁前的能级( E )的能量差：     hν=E-E 

式中ν是光子的频率，h为普朗克常量，等于6.626×10-34J·s 

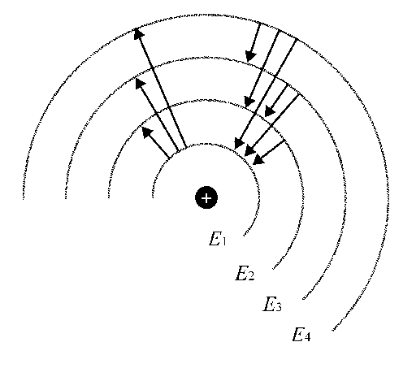
                                               氢原子能级图

玻尔理论成功地解释了原子稳定存在的事实和氢原子光谱:

◆ 在正常状态时，核外电子处于最低的基态，在该状态下运动的电子既不吸收能量，也不放出能量，电子的能量不会减少，因此不会落到原核上，原子不会毁灭。

◆ 原子从外界接受能量时，电子就会跃迁到能量较高的激发态。而处于激发态的电子是不稳定的，它会跃迁回能量较低的轨道 ，同时将能量以光的形式发射出来 ，发射出的光的频率决定于跃迁前后两个轨道间的能量差。由于轨道的能量是不连续的，所发射出的光的频率也是不连续的，因此得到的氢原子光谱是线状光谱。

1923年，法国物理学家de Broglie L 在光的波粒二象性启发下，提出了所有微观粒子如电子、原子等也具有波粒二象性 。他将反映光的二象性的公式应用到微粒上，导出了微观粒子具有波动性的de Broglie关系式：

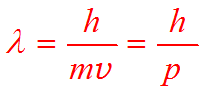
p：微粒的动量

m：微粒的质量

v：微粒的运动速度

λ：微粒波的波长

贝尔电话实验室的Davisson  C J和Germer  L H用电子束代替X射线通过一薄层镍的晶体 （作为衍射光栅），投射到照相底片上，得到了完全类似单色光通过小圆孔那样的衍射图象。 

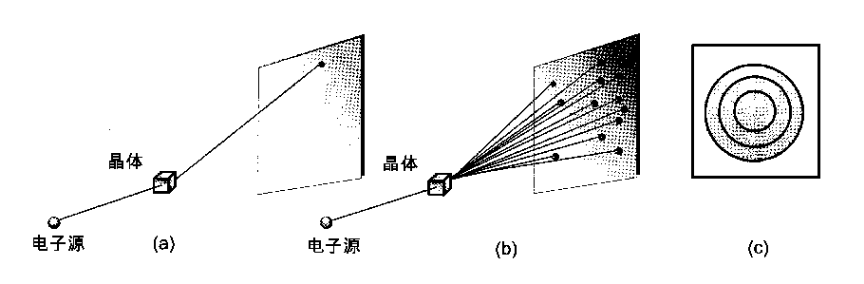
                           电子衍射图

 衍射图像上，亮斑强度大的地方，电子出现的概率大，反之，电子出现少的地方，亮斑强度就弱。

                                    电子衍射图

电子波是概率波，反映电子在空间各区域出现的概率大小。

Heisenberg不确定原理：无法同时确定微观粒子的位置和动量，它的位置越准确，动量（速度）就测得越不准。反之，它的动量测得越准确，位置就越不准确。 

                         x·△px≥h/4π                     

  △ x：为x方向坐标的测不准量(误差)

      △ px：为x方向的动量的测不准量

           h：是普朗克常量。 

 对于质量为0.01 kg 的子弹，运动速率为1000m·s，若速率的不确定程度为其运动速率的 0.1% ，则其位置的不确定程度为。

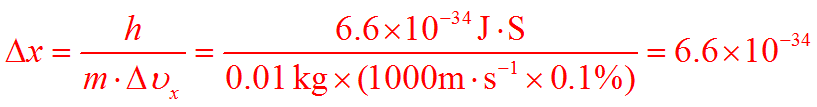
宏观物体的位置不确定程度Δx = m就已经很准确了，这样小的位置不确定程度可以忽略不计。