本节微课教师由教材的思考题入手导，通过对题目的分层分析，让学生对这节课的知识做好了充足的储备。由教材导学引出相关知识点，并结合两个探究板块，将平行线分线段成比例运用到了图形相似的证明中。

本节微课注重了对教材的深度挖掘，突出了新旧知识间的有机连接，帮助学生完善整个知识框架与结构，最后教师对与平行线相关的相似图形与基本结论进行了整合分类。

本节微课教师首先对相似三角形相关概念进行回顾，再依据全等三角形的判定定理，让同学通过旧知，提出问题，最后类比边边边的判定定理，研究相似三角形的判定定理（SSS）。既让学生感受到已学的知识经验对于数学学习的重要性，又亲历新知识的形成过程。教师再借用各类题目运用该判定定理，便于学生理解掌握新知。

本节微课注重了新旧知识的有机连接，及从特殊到一般的过渡，突出了定理的辨析与运用。最后教师对判定相似三角形的常用方法进行了梳理归纳，再配以例题、习题进行巩固。

本节微课教师首先对相似三角形进行回顾，再类比全等三角形边角边的判定定理，研究两边和夹角的关系探索三角形相似，并探究对应边夹角的重要性。既让学生感受到已学的知识经验对于数学学习的重要性，又亲历新知识的形成过程及证明过程。教师再借用大量习题运用该判定定理，加强学生的理解和掌握。

本节微课注重了新旧知识的有机连接，突出了定理的辨析与运用。最后教师对基本的相似三角形的形成、变化及发展过程，进行梳理归纳，帮助学生进行整合分类，完善其知识结构。

本节微课教师首先进行知识回顾，带领学生复习已经学过判定三角形相似的四种方法，以旧知识入手，提出新问题，让学生通过两副不同的三角尺探究出新的判定定理。在探究过程中充分锻炼了学生从实物到图形，从生活到数学的抽象过程。

本节微课注重了从特殊到一般的过渡，突出了定理的辨析与应用，最后教师对图形的相似的判定定理及图形的基本变化过程进行了总结与归纳，再配以例题、习题进行巩固。

本节课讨论的是相似三角形几何量之间的关系。首先，让学生探究相似三角形的对应高、对应中线和对应角平分线的比与相似比之间的关系. 接下来，以对应高为例进行了证明，并得出了“相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比”的结论，并将这个结论推广到“相似三角形对应线段的比等于相似比”.然后，探讨了相似三角形面积比与相似比的关系，并用代数计算方法证明了相似三角形的面积比等于相似比. 最后，通过例题、习题的设计进一步巩固所学知识，并让学生知道，当遇到求三角形中的未知几何量问题时，通常可以先判定两个三角形相似，再利用相似三角形的性质求解.

本届微课围绕相似三角形的性质这一内容展开，并以它为主线贯穿整节课，由浅入深，环环相扣，紧扣本节课的学习目标，难易结合，重点突出，突破难点，能促使不同层次的学生发展.

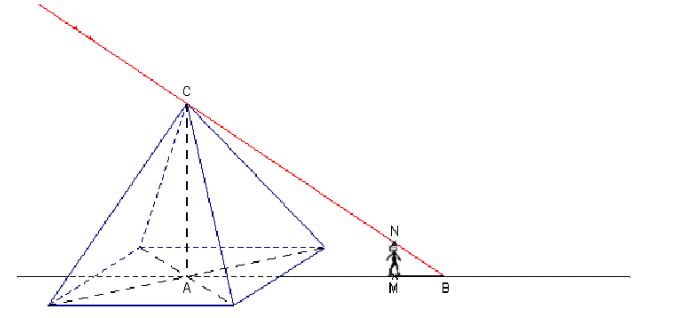
本节微课教师从实际问题入手，引出本节课的学习目标：如何利用三角形的相似，来解决生活中不能直接测量的物体长度的问题。接着通过探究如何测量金字塔的高度，激发学生学习热情，引发学生积极思考，让学生体会在“测高”的过程中利用太阳光的影子和平面镜反射来构造相似三角形，从而归纳出测量高度的方法。再通过测量旗杆、建筑物的高度等实例进一步巩固和提高。

本节微课充分发挥了学生的主体地位，注重学生的自主探索，引导学生认真观察图形，从实际问题中抽象出几何图形，鼓励学生动手操作、演示、证明和计算，帮助学生更好的体会数学建模的思想方法。

本节微课通过实例说明相似三角形在测量方面的应用，帮助学生进一步熟练运用相似三角形的判定定理和性质解决实际问题，增强了学生分析问题、解决问题的能力。

泰勒斯测量金字塔高度

泰勒斯（Thales，约公元前624年—公元前546年），又译为泰利斯，公元前7至6世纪的古希腊时期的思想家、科学家、哲学家，希腊最早的哲学学派——米利都学派（也称爱奥尼亚学派）的创始人，被称为“科学和哲学之祖”。泰勒斯是古希腊及西方第一个有记载有名字留下来的自然科学家和哲学家，泰勒斯的学生有阿那克西曼德、阿那克西美尼等。

    泰勒斯在数学方面划时代的贡献是引入了命题证明的思想。它标志着人们对客观事物认识从经验上升到理论，这在数学史上是一次不寻常的飞跃。在数学中引入逻辑证明，它的重要意义在于：保证了命题的正确性；揭示了各定理之间的内在的联系，使数学构成一个严密的体系，为进一步发展打下基础；使数学命题具有充分的说服力，令人深信不疑。

    证明命题是希腊几何学的基本精神，而泰勒斯就是希腊几何学的先驱。他把埃及的地面几何演变成平面几何学，并发现了许多几何学的基本定理，如“直径平分圆周”、“等腰三角形底角相等”、“两直线相交、其对顶角相等”、“半圆所对的圆周角是直角”、“相似三角形对应边成比例”等，并将几何学知识应用到实践中去。

    据说，埃及的大金字塔修成一千多年后，还没有人能够准确的测出它的高度。由于金字塔是法老们的陵墓，人们对金字塔十分敬畏，没有人敢登上金字塔进行测量，所以人们根本没有办法直接测量它们的高度。法老王一直为没有人能够测量出“金字塔”的高度而苦恼。泰勒斯知道了这件事情，在一番思考以后，他就想出一个测量金字塔的办法。为此，他去见了法老王，说他能够测量出来。

在一个阳光明媚的日子里，他和他的助手及法老王一同来到金字塔的下面，准备测量。他首先测出自己的身高，然后站在阳光里，这样地面上就出现了他的影子。当影子的长度等于自己身高的时候，他就让助手测出金字塔的塔底中心到金字塔影子顶端的距离，这样他就报出了金字塔的确切高度。在法老的请求下，他向大家讲解了如何从“影长等于身长”推到“塔影等于塔高”的原理，也就是今天所说的相似三角形的性质。

古希腊人利用和他相近的办法，用一根竹杆甚至还测出了地球的半径，并且和现在的数值相差不大，这在当时可是一项很了不起的成就。