在项目六中我们提到了神经网络算法,神经网络在识别图像和语音、识别手写、理解文本、图像分割、对话系统、自动驾驶等领域不断打破纪录。
该算法是一种简单易实现的、很重要的机器学习算法。在项目六中我们直接调用scikit-learn中实现的一种神经网络算法实现了鸢尾花的分类。本节将通过TensorFlow实现自定义的不同神经网络,并在鸢尾花Iris数据集上进行模型训练。神经网络算法对所选择的参数是敏感的。在应用中,通过调整参数,了解不同的学习率、损失函数和优化对模型训练结果的影响。
任务1:设计一个具有单个隐藏层的神经网络,如图所示,使用鸢尾花Iris数据集,实现输入三个值,即花萼长度、花萼宽度和花瓣长度,来预测输出值花瓣宽度。
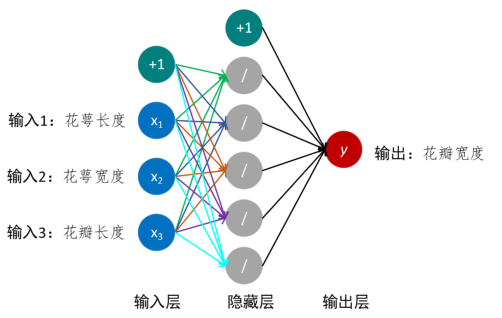
TensorFlow的Windows版目前只支持Python3.5以上(自1.2起)。
| #coding:utf-8
import numpyas np
import pandas as pd
import matplotlib.pyplotas plt
import tensorflowas tf
from sklearn.model_selection import train_test_split
from sklearnimport preprocessing
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 数据读取
df= pd.read_csv('iris.csv', delimiter=',')
# 对类别进行数值化处理
le = preprocessing.LabelEncoder()
df['Cluster'] = le.fit_transform(df['Species'])
# 三个输入值
x = df[['SepalLengthCm','SepalWidthCm','PetalLengthCm']]
# 一个输出值
y = df[['PetalWidthCm']]
# 设置种子使得结果可复现
sess = tf.Session()
# 如何设置随机种子,需要考虑
seed = 2
tf.set_random_seed(seed)
np.random.seed(seed)
# 创建训练集与测试集的划分
x_train, x_test,y_train, y_test = train_test_split(x, y, train_size = 0.8, test_size = 0.2)
# 添加三个占位符,用做输入(即花萼长度、花萼宽度和花瓣长度)
x_data = tf.placeholder(shape=[None, 3], dtype=tf.float32) # 添加一个占位符,用输出(即花瓣宽度)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 单个隐藏层:五个节点(这里我们设计了五个节点)
hidden_layer_nodes = 5
weights = tf.Variable(tf.random_normal(shape=[3, hidden_layer_nodes]))
biase = tf.Variable(tf.random_normal(shape=[hidden_layer_nodes]))
# 隐藏层输出,即输出层的输入
# 激励函数:
hidden_output = tf.nn.relu(tf.add(tf.matmul(x_data,weights),biase))
# 结果层
weights = tf.Variable(tf.random_normal(shape=[hidden_layer_nodes, 1]))
biase = tf.Variable(tf.random_normal(shape=[1]))
# 激励函数使用的是ReLu,它可快速收敛,但容易出现极值
final_output = tf.nn.relu(tf.add(tf.matmul(hidden_output, weights),biase))
# 定义损失函数,采用模型输出和预期值差值的L1范数平均
loss = tf.reduce_mean(tf.abs(y_target - final_output))
# 标准梯度下降优化算法,使用梯度下降优化器来基于损失值的导数去更新权重。
# 优化器采用一个学习率来调整每一步更新的大小,注意学习率的调参
my_opt = tf.train.GradientDescentOptimizer(learning_rate=0.001)
# 最小化损失函数
train_step = my_opt.minimize(loss)
# 初始化
init = tf.global_variables_initializer() # 进行
sess.run(init)
loss_vec = [] #训练操失
test_loss = [] #测试操失
# 遍历迭代训练模型
for i in range(2000):
# 训练
sess.run(train_step, feed_dict={x_data:x_train, y_target:y_train})
# 训练数据评估模型
temp_loss = sess.run(loss, feed_dict= {x_data:x_train, y_target:y_train})
loss_vec.append(np.sqrt(temp_loss))
# 测试数据评估模型
test_temp_loss = sess.run(loss, feed_dict= {x_data:x_test, y_target:y_test})
test_loss.append(np.sqrt(test_temp_loss)) # 输出损失
if (i+1)%500 == 0:
print('迭代次数:' + str(i+1) + '。损失: ' + str(temp_loss))
# 输出预测精确度
y_pred = sess.run(final_output,feed_dict={x_data:x_test})
print("花瓣宽度预期差值(百分比):{}%".format(np.mean(abs(y_test-y_pred)*100/y_test)))
plt.plot(loss_vec, 'k-', label ='训练损失')
plt.plot(test_loss, 'r--', label ='测试损失')
plt.title('损失')
plt.xlabel('迭代次数')
plt.ylabel('损失')
plt.legend(loc='upper right')
plt.show() |
神经网络算法的一个重要的技术是“反向传播”。反向传播是一种基于学习率和损失函数返回值来更新模型变量的过程。神经网络算法另外一个重要的特性是非线性激励函数。因为大部分神经网络算法仅仅是加法操作和乘法操作的结合,所以它们不能进行非线性数据样本集的模型训练。为了解决该问题,在神经网络算法中会使用非线性激励函数,这将使得神经网络算法能够解决大部分非线性的问题。
一般地,神经网络算法常用激励函数有两类,第一类是形状类似sigmoid的激励函数,包括反正切激励函数、双曲正切函数、阶跃激励函数等;第二类是形状类似ReLU的激励函数,包括softplus激励函数、leak ReLU激励函数等。其中,sigmoid激励函数具有良好的梯度控制;而ReLu快速收敛,容易出现极值。需要根据实际应用情况确定对应的方法。
根据显示的结果,调整参数,包括使用的节点数、学习率、损失函数、激励函数、迭代次数等。

如图所示,在不断迭代过程中,“反向传播”的特性使得损失函数在不断降低。为优化模型,需要根据结果,修改相应参数,以获得更好的模型。
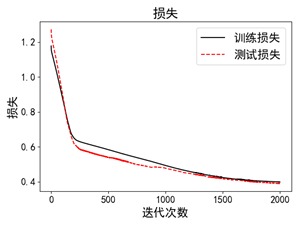
在有新的数据产生时,就可以使用模型做预测的应用。





