事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。
在电影产业中,一个电影的评分可能与多项因素相关。假设评分与电影日均票房、放映天数、电影类型等因素有关(此处我们仅关注是否爱情片),我们在使用回归分析时就需要用多元回归对评分进行相关分析与预测。
任务3:根据电影日均票房、放映周期、电影类型(是否爱情片),使用多元线性回归分析模型来预测电影评分。
| # 读入数据
df = pd.read_csv('film.txt', delimiter=';')
df =df[['影片类型','上映时间','闭映时间', '票房/万','评分']]
# 数据清洗
df = df.dropna()
df = df.drop_duplicates()
# 数据整理
df['上映时间'] = pd.to_datetime(df['上映时间'])
df['闭映时间'] = pd.to_datetime(df['闭映时间'])
df['放映周期'] = (df['闭映时间'] - df['上映时间']).dt.days + 1
df['票房/万'] = df['票房/万'].astype(float64)
df['日均票房/万'] = df['票房/万']/df['放映周期']
df['评分'] = df['评分'].astype(float64)
df['是否爱情片']= df['影片类型'].str.contains('爱情').astype(str)
name_to_type = {'True':'1','False':'0'};
df['影片类型(爱情)']=df['是否爱情片'].map(name_to_type);
df.head() |
准备好的部分数据如图所示: 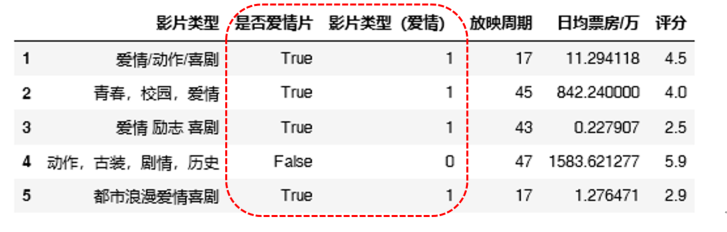
# 拆分训练集和测试集
x_train, x_test,y_train, y_test=train_test_split(df[['影片类型(爱情)','放映周期','日均票房/万']],df[['评分']],train_size=0.8, test_size=0.2)
# 建立线性回归模型
regr = linear_model.LinearRegression()
# 数据拟合
regr.fit(x_train, y_train)
# 系数、截距
print('系数:',regr.coef_)
print('截距:',regr.intercept_)
# 给出待re预测的一个特征
y_pred = regr.predict(x_test)
plt.plot(range(len(y_pred)),y_pred,'red', linewidth=2.5,label=u"预测值",linestyle='--')
plt.plot(range(len(y_test)),y_test,'green',label=u"测试值")
plt.legend(loc=2) plt.ylabel('评分')
# 显示预测值与测试值曲线
plt.show() |
| 系数: [[-1.93644687e+00 -1.29725765e-02 4.03645528e-04]] 截距: [6.50362603] |
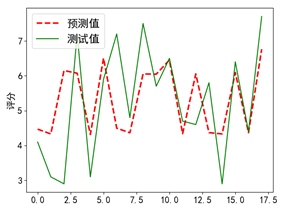
多元线性回归操作实现讲解详见以下视频:
进阶:sklearn库中数据预处理方法LabelEncoder实现标签映射
sklearn.preprocessing.LabelEncoder()即标准化标签,将标签值统一转换成range(标签值个数-1)范围内。简单来说,LabelEncoder是对不连续的数字或者文本进行编号。那么上述映射的复杂代码,可以简化。LabelEncoder标记编码转换的使用代码如下:
| from sklearnimport preprocessing
# 对电影类别进行数值化处理
le = preprocessing.LabelEncoder()
new_df['影片类型(爱情)'] = le.fit_transform(new_df['是否爱情片']) |
转换后的电影类型编码数据(已框出)如下图所示。 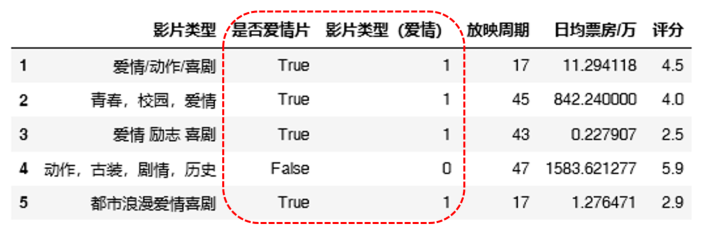
数据预处理中的标签映射操作讲解详见以下视频:





