一元线性回归的基本概念
回归只涉及两个变量的,称为一元回归。一元回归的主要任务是从两个相关变量中的一个变量(放映天数)去估计另一个变量(日均票房),被估计的变量(日均票房)称因变量,可设为Y;自变量设为X(放映天数)。回归分析就是要找出一个数学模型Y = f(X),使得从X可以估计Y。此时,Y可以用函数去计算。当Y=f(X)的形式是一个直线方程时,称为一元线性回归。这个方程一般可表示为Y=A+BX。A为截距,B为系数。
一元线性回归基本概念介绍见如下视频:
任务描述
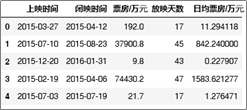
电影数据中,统计量日均票房=累计票房÷放映天数。当每日票房不足百万时一般就将会在接下来的一周左右下档。我们可能会联想推测,日均票房与放映天数是否存在一定的相关性?在本节中,我们将通过一元线性回归方法对两项数据进行简要的相关性分析,探讨是否可以在通过计划放映天数预测电影的票房。
一元线性回归实现基本原理与过程说明见以下视频:
分项任务2.1:根据放映天数,使用一元线性回归分析预测电影日均票房。
步骤一:数据读取与整理
# 用pandas读取文件,并用分号隔开
import pandas as pd
df= pd.read_csv('film.txt', delimiter=';')
# 筛选指定内容
df=df[['上映时间','闭映时间', '票房/万']]
# 除去带有空值的行
df=df.dropna()
# 转成时间类型
df['上映时间'] =pd.to_datetime(df['上映时间'])
df['闭映时间'] =pd.to_datetime(df['闭映时间'])
# 计算电影放映天数
df['放映天数']=(df['闭映时间'] -df['上映时间']).dt.days+ 1
# 票房数据转换为浮点型
df['票房/万'] =df['票房/万'].astype(float)
# 计算日均票房
df['日均票房/万'] =df['票房/万']/df['放映天数']
# 重置索引列,不添加新的列
df = df.reset_index(drop=True)
df.head()
步骤二:使用一元线性回归分析
from sklearnimportlinear_model
# 设定x和y的值
x = df[['放映天数']]
y = df[['日均票房/万']]
# 初始化线性回归模型
regr = linear_model.LinearRegression()
# 拟合
regr.fit(x, y)
步骤三:可视化分析结果
import matplotlib.pyplotas plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 可视化
# 定义图表标题等
plt.title('放映天数与票房关系图(一元线性回归分析)')
plt.xlabel('放映天数')
plt.ylabel('日均票房收入\万元')
plt.scatter(x, y, color='black')
# 画出预测点,预测点的宽度为1,颜色为红色
plt.scatter(x, regr.predict(x), color='red',linewidth=1 , marker = '*')
plt.legend(['原始值','预测值'], loc= 2)
plt.show()
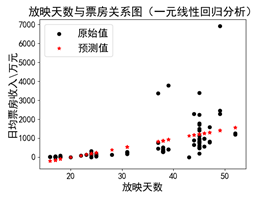
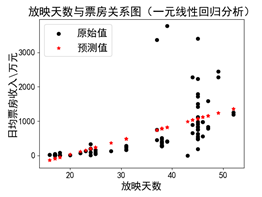
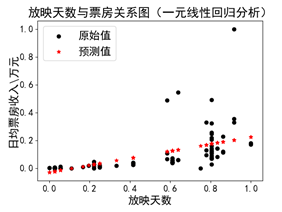
(a)使用原始数据 (b)去除“奇异点”
一元线性回归实现整体步骤讲解见以下视频:
思考进阶(1):异常值处理
线性回归的主要问题是对异常值敏感,在真实世界的数据收集过程中,经常会碰到错误的度量结果。上图(a)中,右上角的数值对于模型来讲是一个“奇异点”(df = df[df['日均票房/万']<5000]),在数据清洗、准备阶段,可以将该项值去掉以提高模型的准备性。图(b)中是对“奇异点”去除后的结果。
这些异常值的处理方法常用有四种:
1.删除含有异常值的记录
2.将异常值视为缺失值,交给缺失值处理方法来处理
3.用平均值来修正
4.不处理
项目中采用第1 种方法,异常值处理操作详见以下视频:
思考进阶(2):归一化处理
在机器学习领域中,不同评价指标(即特征向量中的不同特征就是所述的不同评价指标)往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果,为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。
原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。其中,最典型的就是数据的归一化处理。
简而言之,归一化的目的就是使得预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而消除样本数据不同量纲导致的不良影响。
在本项目中,需要将特征缩放到合理的大小是非常重要的。范围缩放(scaling)后,所有的数据特征值都位于指定范围内。我们将日均票房、放映天数进行范围绽放至[0,1]。
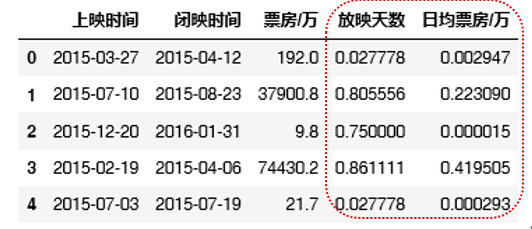
分项任务2.2:将日均票房、放映天数进行范围绽放至[0,1],即归一化处理。
步骤一:数据缩放
from sklearn.preprocessingimport minmax_scale
df['日均票房/万'] = minmax_scale(df['日均票房/万'])
df['放映天数'] = minmax_scale(df['放映天数'])
df.head()
步骤二:可视化结果
观察上述两张结果图的不同,形状相同,但是比例尺不同。
步骤三:可视化进阶,画出预测线
#定义x的最小值
x_min = x.values.min() - 0.1
# 定义x的最大值
x_max = x.values.max() + 0.1
#定义一个序列,最小值是x_min,最大值是x_max,步长为0.005
step = 0.005
x_new = np.arange(x_min,x_max,step).reshape(-1, 1)
plt.title(u'放映天数与票房关系图(一元线性回归分析)')
plt.xlabel(u'放映天数')
plt.ylabel(u'日均票房收入\万元')
plt.scatter(x, y, color='black')
plt.scatter(x_new, regr.predict(x_new),s=1, color='red',linewidth=2)
plt.legend(['原始值','预测值'], loc= 2)
plt.show()
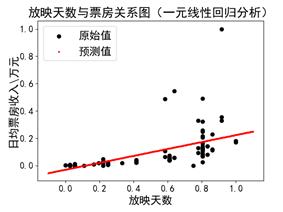
分项任务2.3:以8:2拆分训练集与测试集的切分,并对模型进行评估。
现实生活中,计算机没办法像人类一样认识事物,所以人类一直致力于这方面的研究来提高计算机认知事物的能力。在机器学习领域,人们已经开发了许多方法以实现计算机识别能力,比如支持向量机(SVM)等,还有目前最火且具有最高识别度的还是深度学习。举个例子,假如我们需要识别一辆小汽车。那么我们就需要有大量的小汽车图片(训练数据),当有足够多的数据时,我们就可以进行机器学习了。需要告诉计算机,这些数据都是小汽车。计算机通过算法知道什么是小汽车,具备哪些特征。学习完成后,我们就可以放入已有的其他图片(测试数据),计算机会把这些图片作为输入,通过训练后模型进行判断,并告诉我们哪些是小汽车,哪些不是小汽车。
因此,一般将样本分成独立的三部分,分别为:训练集(training set),验证集(validation set)和测试集(test set)。其中,训练集用于建立模型,简单地说就是通过训练集的数据确定拟合曲线的参数。验证集用来做模型选择(model selection),即做模型的最终优化及确定的,用来辅助模型构建,它是可选的。而测试集则是用来检验最终选择的模型的性能。
在实际应用中,一般只将数据集分成两类,即训练集和测试集。大多数应用并不涉及验证集,而是通过测试集来验证模型的准确性。
本节主要介绍sklearn里如何将已有的数据分为训练集和测试集,以及如何检验模型的准确度。以上述代码中,我们将所有的数据都用来做了训练。当然,我们可以将其中的一部分抽取出来作为测试集。假设我们需要随机抽取80%的数据用来做训练,20%的数据来判断模型的准确性。这时,可利用skearn中的函数来实现数据集的切分。
关于数据集切分的内容介绍视频如下:
步骤一:编码实现电影数据拆分,代码如下:
| from sklearn.model_selection import train_test_split #拆分训练集和测试集 |
步骤二:模型训练,代码如下:
| # 建立线性回归模型 |
步骤三:模型使用,代码如下:
| # 给出测试集的预测结果 |
步骤四:预测结果评估与可视化,代码如下:
| plt.title(u'预测值与实际值比较(一元线性回归)') # 画出预测值折线 # 显示测试值折线 |
步骤五:运行代码,显示结果
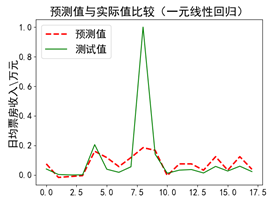
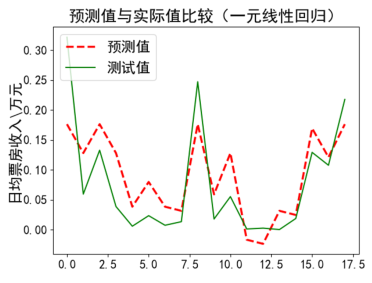
(a)第一次运行 (b)第二次运行


