-
1.1《爱因斯坦文集》序
-
1.2自述
-
1.3自述片断
-
1.4失业的痛苦和探索自然界统一性的乐趣——1901年4月14日给M.格罗斯曼的信
-
1.5生活的一个侧面——1903年1月给贝索的信
-
1.5.1附录一:《爱因斯坦给M.贝索的信选译》选编说明
-
1.5.2附录二:贝索,爱因斯坦最亲密的朋友——《爱因斯坦给M.贝索的信选译》编后记
-
1.61905年春天的四项研究——1905年5月给C.哈比希特的信
-
1.7论我们关于辐射的本质和组成的观点的发展
-
1.8也许量子问题的答案就藏在这里——1909年12月31日给贝索的信
-
1.9关于比热理论——1911年5月13日给贝索的信
-
1.10对第一次索耳未会议的印象——1911年12月26日给贝索的信
-
1.11红外线的吸收及其他——1912年2月4日给贝索的信
-
1.12作为研究者的麦克斯·普朗克
-
1.13相对论的引力论和马赫原理——1913年6月25日给E.马赫的信
-
1.14物理学家对引力论的态度——1913年底给贝索的信
-
1.15我不怀疑引力理论的正确性——1914年3月给贝索的信
-
1.16理论物理学的原理——在普鲁士科学院的就职讲话
-
1.17评H.A.洛伦兹的《相对性原理》
-
1.18科学方面两个好消息——1915年2月12日给贝索的信
-
1.19关于广义相对论——1915年11月28日给A.索末菲的信
-
1.20如今实现了最大胆的梦想——1915年12月10日给贝索的信
-
1.21关于广义相对论——1915年12月21日给贝索的信
-
1.22引力论获得巨大成功——1916年1月3日给贝索的信
-
1.23恩斯特·马赫
-
1.24关于有限宇宙的设想——1916年5月14日给贝索的信
-
1.25悼念卡尔·施瓦兹希耳德
-
1.26关于辐射的量子理论——1916年8月11日给贝索的信
-
1.27续论辐射的量子论——1916年8月24日给贝索的信
-
1.28可以肯定光量子的存在——1916年9月6日给贝索的信
-
1.29空间和时间的客观意义之所在——1916年10月31日给贝索的信
-
1.30为什么要提出闭合空间的假设——1916年12月中旬给贝索的信
-
1.31《狭义与广义相对论浅说》中的一个片断
-
1.31.1几何学命题的物理意义
-
1.32爱因斯坦给德西特的信(1916—1918年)——卡拉·卡恩和弗朗兹·卡恩报道
-
1.33关于宇宙学和其他——1917年3月9日给贝索的信
-
1.34对马赫的看法——1917年5月13日给贝索的信
-
1.34.1附:贝索1917年5月5日给爱因斯坦的信
-
1.35关于辐射量子的实在性和广义相对论的能量原理——1918年7月29日给贝索的信
-
1.36马里安·冯·斯莫卢霍夫斯基
-
1.37探索的动机——在普朗克六十岁生日庆祝会上的讲话
-
1.38康德的《绪论》读后感——1918年6—7月间给M.玻恩的信
-
1.39关于魏耳的理论和宇宙学问题——1918年8月20日给贝索的信
-
1.40理论必须以经验事实为依据——1918年8月28日给贝索的信
-
1.41黎曼几何也有它在地球上的起源——1918年9月8日给贝索的信
-
1.42应当对量子论的成功感到羞愧——1919年6月4日给M.玻恩的信
-
1.43什么是相对论?
-
1.44关于魏耳理论及其他——1919年12月12日给贝索的信
-
1.45不愿意放弃完全的因果性——1920年1月27日给M.玻恩的信
-
1.46理论和实验——《狭义与广义相对论浅说》德文第10版附录
-
1.47相对论的认识论观点以及闭合空间问题——1920年4月24日给M.索洛文的信
-
1.48以太和相对论
-
1.49我对反相对论公司的答复
-
1.50对“反相对论公司”的斗争——1920年9月6日给A.索末菲的信
-
1.50.1附:A.索末菲1920年9月3日给爱因斯坦的信
-
1.51对几种统一场论的评价——1922年6月6日给H.魏耳的信
-
1.52几何学和经验
-
1.53相对论发展简述
-
1.54《相对论的意义》中的两个片断
-
1.54.1相对论以前物理学中的空间和时间
-
1.54.2广义相对论
-
1.55关于相对论
-
1.56评W.泡利的《相对论》
-
1.57对康德哲学和马赫哲学的看法(报道)
-
1.58论理论物理学的现代危机
-
1.59《爱因斯坦全集》日文版序言
-
1.60关于诺贝尔奖——1923年1月11日给N.玻尔的信
-
1.60.1附:N.玻尔1922年11月11日给爱因斯坦的信
-
1.61尼耳斯·玻尔
-
1.62大自然赋予我们的是渴望多于智慧——1923年5月底给H.魏耳的明信片
-
1.63相对论的基本思想和问题
-
1.64评J.温特尼茨的《相对论和认识论》
-
1.65关于场论以及国际联盟——1924年1月5日给贝索的信
-
1.66反对电子有自由意志的想法——1924年4月29日给玻恩夫妇的信
-
1.66.1附:M.玻恩1925年7月15日给爱因斯坦的信
-
1.67在量子问题上我相信自己走的路是正确的——1924年5月24日给贝索的信
-
1.68对玻尔等人否定守恒定律的评论——1924年5月31日给P.埃伦菲斯特的信
-
1.69卢克莱修《物性论》德译本序
-
1.70对恩格斯《自然辩证法》手稿的意见
-
1.71非欧几里得几何和物理学
-
1.72对魏耳、爱丁顿、舒滕工作的评价——1925年6月5日给贝索的信
-
1.73关于仿射场论——1925年7月28日于日内瓦给贝索的信
-
1.74对薛定谔工作和海森伯-玻恩工作的评价——1926年4月26日给E.薛定谔的信
-
1.75关于量子力学的哲学背景问题同海森伯的谈话(报道)
-
1.76对统一场论以及对薛定谔和海森伯-狄拉克工作的评价——1926年8月21日给A.索末菲的信
-
1.77对薛定谔工作和对爱丁顿工作的评论——1926年11月28日给A.索末菲的信
-
1.78我深信上帝不是在掷骰子——1926年12月4日给M.玻恩的信
-
1.79对贝索的评价——1926年12月21日给H.仓格尔的信
-
1.80对米勒实验和量子力学的看法——1925年12月25日给贝索的信
-
1.81牛顿力学及其对理论物理学发展的影响
-
1.82对于量子理论的意见——在第五次索耳未会议上的发言
-
1.83量子力学的真理性同古典光学差不多——1927年11月9日给A.索末菲的信
-
1.84物理学的基本概念及其最近的变化
-
1.85测不准关系和海森伯-玻尔的绥靖哲学——1928年5月31日给E.薛定谔的信
-
1.86评M.E.梅耶松的《相对论的演绎法》
-
1.87统一场论的重大发展——1929年1月5日给贝索的信
-
1.88感谢斯托多拉
-
1.89关于科学的真理
-
1.90我信仰斯宾诺莎的上帝
-
1.91空间-时间
-
1.92物理学中的空间、以太和场的问题
-
1.93关于实在的本性问题同泰戈尔的谈话
-
1.94马赫同相对论的关系——1930年9月18日给A.魏纳的信
-
1.95约翰内斯·开普勒
-
1.96宗教和科学
-
1.97科学的宗教精神
-
1.98论科学
-
1.99牛顿的《光学》序
-
1.100量子力学中过去和未来的知识 同R.C.托耳曼和B.波多耳斯基合写
-
1.101关于螺旋星云红移的发现——1931年3月1日给贝索的信
-
1.102关于统一场论和经济问题的讨论——1931年10月30日给贝索的信
-
1.103麦克斯韦对物理实在观念发展的影响
-
1.104关于测不准关系(报道)
-
1.105在哥伦比亚大学的讲话
-
1.106关于因果性和自由意志问题同J.墨菲的谈话
-
1.107祝贺阿诺耳德·柏林内尔七十岁生日
-
1.108评理论物理学中问题的提法上的变化
-
1.109关于理论物理学的方法
-
1.110广义相对论的来源
-
1.111保耳·埃伦菲斯特的工作及其为人
-
1.112能认为量子力学对物理实在的描述是完备的吗?——同B.波多耳斯基和N.罗森合著
-
1.113生活和工作的感受——1935年夏给妹妹的信
-
1.114关于量子力学描述的完备性问题——1935年9月11日给K.R.波普的信
-
1.115悼念玛丽·居里
-
1.116物理学和实在
-
1.116.1一 关于科学方法的一般考查
-
1.116.2二 力学以及把力学作为全部物理学基础的企图
-
1.116.3三 场的概念
-
1.116.4四 相对论
-
1.116.5五 量子论和物理学的基础
-
1.116.6六 相对论和微粒
-
1.116.7总 结
-
1.117悼念马尔塞耳·格罗斯曼——1936年给格罗斯曼夫人的信
-
1.118《物理学的进化》的两个片断——同L.英费耳德合著
-
1.118.1哲学背景
-
1.118.2物理学和实在
-
1.119我还是以昔日的喜悦努力钻研问题——1937年6月9日给贝索的信
-
1.120引力问题使我从怀疑的经验论转向信仰唯理论——1938年1月24日给C.兰佐斯的信
-
1.121关于实证论的统治及其他——1938年4月10日给M.索洛文的信
-
1.122关于完备的描述和实在的问题——1939年8月9日给E.薛定谔的信
-
1.123关于理论物理学基础的考查
-
1.124科学的共同语言
-
1.125伐耳特·能斯特的工作及其为人
-
1.126统一场论方面的一个新尝试——1942年8月给贝索的信
-
1.127爱萨克·牛顿
-
1.128论伯特兰·罗素的认识论
-
1.128.1附:罗素的答复
-
1.129客观世界的完备定律及其他——1944年9月7日给M.玻恩的信
-
1.130关于数学领域的创造心理——给J.阿达马的信
-
1.131关于哲学和科学问题的谈话(报道)——1945年1月同A.施特恩的谈话
-
1.132关于宇宙学问题的评注——《相对论的意义》第二版(1945年)的附录
-
1.133以广义相对论为根据的空间结构——《狭义与广义相对论浅说》英译本第14版(1946年)的附录
-
1.134质能相当性的初浅推导
-
1.135E=mc^2:我们时代最迫切的问题
-
1.136R.凯泽尔的《斯宾诺莎》序
-
1.137悼念保耳·朗之万
-
1.138物理学应当阐明时间和空间中的实在——1947年3月3日给M.玻恩的信
-
1.139对马赫的评价及其他——1948年1月6日给贝索的信
-
1.140对玻恩《关于因果和机遇的自然哲学》书稿的意见——1948年3月18日给M.玻恩的信及其附件
-
1.140.1附件:对《关于因果和机遇的自然哲学》的最后一章《形而上学的结论》的批注
-
1.141悼念麦克斯·普朗克
-
1.142量子力学和实在
-
1.143为《量子力学和实在》一文给M.玻恩的信
-
1.144关于托勒玫、亚里士多德、广义相对论场论及其他——1948年11月25日给M.索洛文的信
-
1.145相对性:相对论的本质
-
1.146对批评的回答 对汇集在论文集《阿耳伯特·爱因斯坦:哲学家-科学家》中各篇论文的意见
-
1.147七十岁生日时的心情——1949年3月28日给M.索洛文的信
-
1.148《伽利略在狱中》读后感——1949年7月4日给麦克斯·布罗德的信
-
1.149对量子力学的看法——1949年7月24日给贝索的信
-
1.150关于统一场论——1949年8月16日给贝索的信
-
1.151要接近事物的本质是万分困难的——1950年4月15日给贝索的信
-
1.152《约翰内斯·开普勒的生平和书信》序
-
1.153关于迈克耳孙实验、相对论起源等问题的谈话(报道)——1950年2月4日同R.S.香克兰的谈话
-
1.154关于广义引力论
-
1.155关于统计论同决定论的对立问题——1950年6月12日给M.索洛文的信
-
1.156关于描述完备性的争论——1950年9月15日给M.玻恩的信
-
1.157关于“实在”问题的讨论——1950年10月13日给H.L.塞缪耳的信
-
1.158实在和完备的描述——1950年12月22日给E.薛定谔的信
-
1.159物理学、哲学和科学进步
-
1.160对实在的理性本质的信赖及其他——1951年1月1日给M.索洛文的信
-
1.161D.D.汝内斯编《斯宾诺莎词典》序
-
1.162五十年思考还不能回答光量子是什么——1951年12月12日给贝索的信
-
1.163关于相对论和量子论问题的谈话(报道)——1952年2月2日同R.S.香克兰的谈话
-
1.164青年时代二三事——1952年3月6日给贝索的信
-
1.165关于相对论诞生的年份——1952年3月11日给C.塞利希的信
-
1.166特殊和一般,直觉和逻辑——1952年3月20日给贝索的信
-
1.167客观世界的规律性和“奇迹”——1952年3月30日给M.索洛文的信
-
1.168关于广义引力论的实验问题——答《通俗科学月刊》——读者的信
-
1.169关于一些基本概念的绪论——祝贺德·布罗意六十岁生日的赠文
-
1.170关于思维同经验的联系问题——1952年5月7日给M.索洛文的信
-
1.171相对论和空间问题
-
1.172《狭义与广义相对论浅说》英译本第15版说明
-
1.173相对论发展的三个阶段——1952年6月给C.塞利希的信
-
1.174生命有个了结,是好事——1952年7月17日给贝索的信
-
1.175否认“实在状态”就落到贝克莱的境地——1952年9月10日给贝索的信
-
1.176要大胆思辨,不要经验堆积——1952年10月8日给贝索的信
-
1.177关于迈克耳孙以及其他问题的谈话(报道)——1952年10月24日同R.S.香克兰的谈话
-
1.178关于迈克耳孙实验对探索相对论的影响问题——纪念迈克耳孙诞辰一百周年的贺信
-
1.17974岁生日答客问(报道)
-
1.180“奥林比亚科学院”颂词——1953年4月3日给C.哈比希特和M.索洛文的回信
-
1.181西方科学的基础与古代中国无缘——1953年4月23日给J.S.斯威策的信
-
1.182关于广义引力论及其他——1953年5月28日给M.索洛文的信
-
1.183创造者H.A.洛伦兹及其为人
-
1.184时间箭头、基本概念的危机及其他——1953年7月29日给贝索的信
-
1.185伽利略《关于托勒玫和哥白尼的两大世界体系的对话》英译本序
-
1.186广义引力论的困难所在——1953年9月22日给贝索的信
-
1.187反对实证论及其他(报道)——1952—1953年间同R.卡尔那普的谈话
-
1.188M.雅梅的《空间概念》序
-
1.189关于量子力学基础的解释的基本见解——纪念M.玻恩退休的赠文
-
1.190“不掷骰子的上帝”及其他——1953年10月12日给M.玻恩的信
-
1.191在哥白尼逝世410周年纪念会上的讲话
-
1.192给玻恩的赠文所引起的争论(一)——1953年12月3日给M.玻恩的信
-
1.192.1附:M.玻恩1953年11月26日给爱因斯坦的信
-
1.193给玻恩的赠文所引起的争论(二)——1954年1月1日给M.玻恩的信
-
1.194给玻恩的赠文所引起的争论(三)——1954年1月12日给M.玻恩的信
-
1.194.1附件:对M.玻恩的回答
-
1.194.2附:W.泡利给M.玻恩的信(1954年3月31日)
-
1.195迈克耳孙实验同相对论的关系——1954年2月9日给F.G.达文波特的信
-
1.196关于相对论的发展——1954年8月10日给贝索的信
-
1.196.1附:贝索1954年10月1—4日给爱因斯坦的信
-
1.197悼念贝索——1955年3月21日给M.贝索的儿子和妹妹的信
-
1.198关于科学史和科学家的谈话(报道)——1955年4月3日同I.B.科恩的谈话
1
爱因斯坦文集
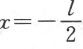 同
同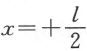 之间才不为零。为了使在间隔两端的ψ函数同在间隔之外的ψ函数连续地相连接这一要求得到满足,那就必须:对于
之间才不为零。为了使在间隔两端的ψ函数同在间隔之外的ψ函数连续地相连接这一要求得到满足,那就必须:对于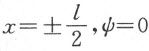 。
。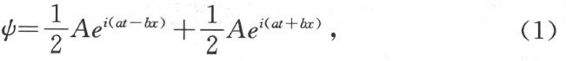

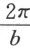 要比l小。
要比l小。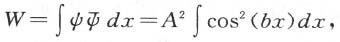
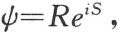
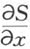 等于零,因而速度也等于零。泡利在四分之一世纪以前就已经提出的对这种理论上的尝试的反对意见,在我们这例子里就显得更加有分量了。速度等于零,是同那个颇有根据的要求相矛盾的,这要求就是:在宏观体系的情况下,运动应当近似地符合于古典力学所得出的结果。
等于零,因而速度也等于零。泡利在四分之一世纪以前就已经提出的对这种理论上的尝试的反对意见,在我们这例子里就显得更加有分量了。速度等于零,是同那个颇有根据的要求相矛盾的,这要求就是:在宏观体系的情况下,运动应当近似地符合于古典力学所得出的结果。