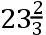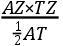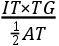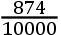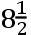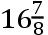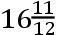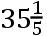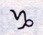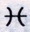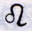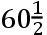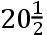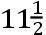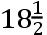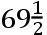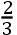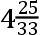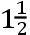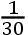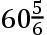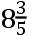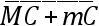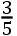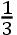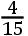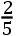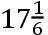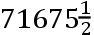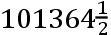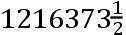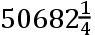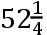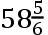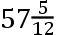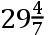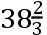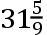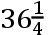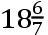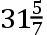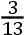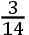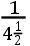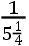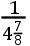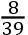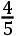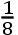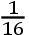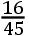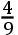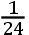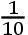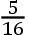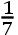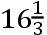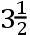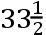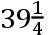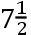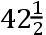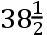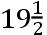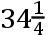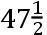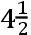论月球的交点的运动
命题 I
离开交点的太阳的平均运动,由太阳的平均运动和那个平均运动之间的几何比例中项确定,太阳由那个平均运动最迅速地退离在方照的交点。
设T为地球所在的位置,Nn为在任意给定的时刻月球的交点线,引一直线KTM与这条直线成直角,直线TA围绕中心以太阳和交点相互退离的角速度转动,如此使得静止的直线Nn和旋转的TA之间的角总等于太阳的和交点的位置之间的距离。现在如果任意的直线TK被分成部分TS和SK,使得它们如同太阳的平均小时运动比在方照时交点的平均小时运动,且设直线TH是部分TS和整体TK之间的比例中项,其中的这条直线[TH]与太阳离开交点的平均运动成比例。
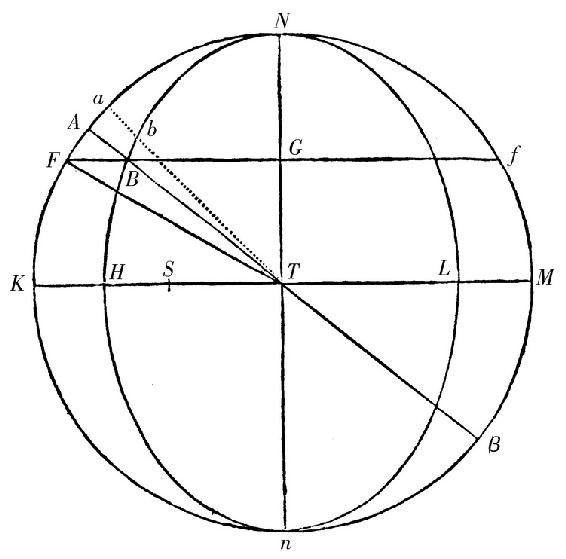
由于以中心T和半径TK画圆NKnM,又以相同的中心和半轴TH和TN画椭圆NHnL,且时间,在此期间太阳经弧Na退离交点,如果引直线Tba,扇形NTa的面积表示在相同的时间交点的和太阳的运动的和。所以,设aA是极短的弧,它由直线Tba按照前面所说的定律转动并在给定的一小段时间均匀地画出,且极小的扇形TAa如同速度的和,太阳和交点在那时以它们分别被移动。但是太阳的速度几乎是均匀的,因为它的小的不等性难以在交点的运动中引入变化。这个和的另一部分,即交点按自身平均量的速度,由《原理》第III卷命题XXXI的系理,在退离朔望时按它离太阳的距离的正弦的二次比被增大;且它的[速度]相对于K处的太阳位于方照时最大,这个速度比太阳的速度与SK比TS有相同的比,这即是如同(TK和TH的平方的差或者)矩形KHM比正方形TH。但椭圆NBH将这个表示两个速度之和的扇形ATa分为两部分ABba和BTb,它们与速度成比例。因为,延长BT至圆上的β,并从点B向长轴落下垂线BG,它向两个方向延长交圆于点F和f,又因为空间ABba比扇形TBb如同矩形ABβ比正方形BT(因那个矩形等于来自TA和TB的正方形的差,由于Aβ在T被平分且在B不被平分)。所以这个比,当空间ABba在K最大时,与矩形KHM比正方形HT的比相同;但交点的最大的平均速度比太阳的速度按照这个比。所以在方照扇形ATa被分成与速度成比例的部分。又因为矩形KHM比正方形HT如同[矩形]FBf比正方形BG,且矩形ABβ等于矩形FBf。所以一小块面积ABba当它最大时比余下的扇形TBb,如同矩形ABβ比正方形BG。但这些小面积的比总如同矩形ABβ比正方形BT;且所以在位置A时的小面积ABba按照BG比BT的二次比,就是按照太阳离交点的距离的正弦的二次比,小于在方照时的类似的小面积。又由于所有小面积ABba的和,即空间ABN如同交点在一段时间的运动,在此期间太阳通过弧NA远离交点。且剩下的空间,即椭圆扇形NTB如同太阳在相同时间的平均运动。所以,因为交点的平均年运动是它在一段时间发生的运动,在此期间太阳完成了自己的循环,交点离开太阳的平均运动比太阳自身的平均运动,如同圆的面积比椭圆的面积,这就是,如同直线TK比直线TH,即TK和TS之间的比例中项;或者得到同样的结果,如同比例中项 TH比直线TS。
命 题 II
给定月球的交点的平均运动求真实运动。
设角A为太阳离交点的平均位置的距离,或者太阳离开交点的平均运动。如果又取角B,它的正切比角A的正切如同TH比TK,这就是,按照太阳的平均小时运动比当交点位于方照时太阳离开交点的平均小时运动的二分之一次比;同一个角B是太阳离开交点的真实位置的距离。因为连结FT,且从上一命题的证明中,角FTN是太阳离交点的平均位置的距离,而角ATN为太阳离交点的真实位置的距离,且这些角的正切彼此如同TK比TH。
系理 因此,角FTA为月球交点的均差,且当这个角的正弦最大时是在八分点,它比半径如同KH比TK+TH。但在其他任意位置A这个均差的正弦比最大的正弦,如同角的和FTN+ATN的正弦比半径:这几乎如同二倍的太阳离交点的平均位置的距离(即2FTN)的正弦比半径。
解释
如果交点的平均小时运动在方照为16″.16.37iv.42v,这就是在整个恒星年中为39°.38′.7″.50,TH比TK按照数9.0827646比数10.0827646的二分之一次比,这就是,如同18.6524761比19.6524761。且所以TH比HK如同18.6524761比1,这就是如同太阳在一个恒星年中的运动比交点的平均运动19°.18′.1″.
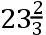 。
。
但是,如果月球的交点的平均运动在20儒略年(54)的386°.50′.15″,作为在观测中得到的并用于月球的理论:则交点的平均运动在一恒星年为19°.20′.31″.58,且TH比HK如同360gr.比19°.20′.31″.58′″,这就是,如同18.61214比1,因此交点在方照的平均小时运动成为16″.18.48iv。且交点在八分点的最大均差为1°.29′.57″。
命题XXXIV 问题XV
求月球的轨道对于黄道的平面的倾角的小时变差。
指定A和a为朔望;Q和q为方照;N和n为交点;P为月球在它自己轨道上的位置,p为那个位置在黄道的平面上的射影,且为mTl为交点的运动的瞬如上。且如果向直线Tm落下垂线PG,连结pG,并延长它直至交Tl于g,再者也连结Pg;角PGp为当月球在P时月球的轨道对黄道的平面的倾角;且角Pgp为相同的轨道在时间的瞬完成之后的倾角,且因此角GPg为倾角的瞬时变化。但这个角GPg比角GTg如同TG比PG和Pp比PG的联合。且所以,如果以一小时代替时间的瞬;由于角GTg(由命题XXX)比角33″.10.33iv如同IT×PG×AZ比ATcub.,则角GPg(或者倾角的小时变差)比33″.10.33iv,如同IT×AZ×TG×[(Pp)/(PG)]比ATcub.,此即所求。
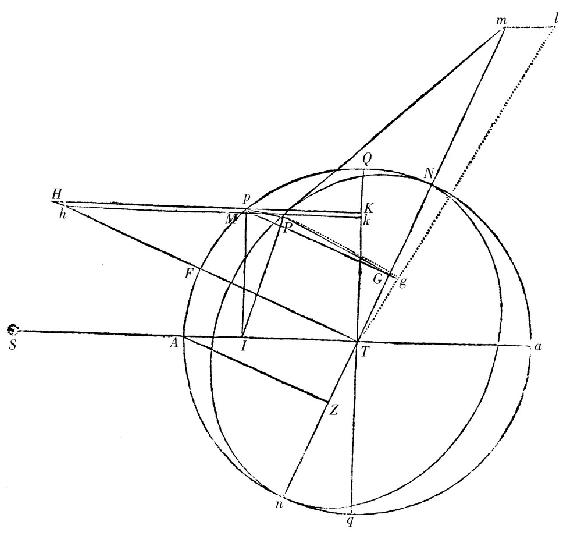
如果假设月球在一条圆轨道上均匀地旋转,这些结果就是如此。但是,如果那个轨道是椭圆,交点的平均运动按照短轴比长轴之比减小,正如上面所阐述的。且倾角的变差也按照相同的比减小。
系理1 如果在Nn上竖立垂线TF,且设pM为月球在黄道的平面内的小时运动,并在QT上落下垂线pK和Mk,延长两者交TF与H和h:则IT比AT如同Kk比Mp,TG比Hp如同TZ比AT,且所以IT×TG等于(Kk×Hp×TZ)/(Mp),这就是,等于面积HpMh乘以比(TZ)/(Mp);所以倾角的小时变差比33″.10.33iv如同HpMh乘以AZ×[(TZ)/(Mp)]×[(Pp)/(PG)]比ATcub.。
系理2 且因此,如果每个小时完成时,地球和交点从它们的新位置被拉回,并总是迅速地返回到它们原来的位置,使得经过一个整周期月它们给定的位置被保持,那个月的时间产生的倾角的整个变差比33″.10.33iv如同点p在一次绕行期间生成的所有面积HpMh的累积,并由适当的符号“+”和“-”连接起来,再乘以AZ×TZ×[(Pp)/(PG)]比Mp×ATcub.。亦即,如同整个圆QAqa乘以AZ×TZ×[(Pp)/(PG)]比Mp×ATcub.,也就是,如同QAqa的周长乘以AZ×TZ×[(Pp)/(PG)]比2Mp×ATq。
系理3 所以,在交点的一个给定的位置,平均小时变差,它从该处均匀地持续一个月能产生那个月变差,比33″.10.33iv,如同AZ×TZ×[(Pp)/(PG)]比2ATq,或者如同Pp×
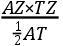 比PG×4AT,亦即(因Pp比PG如同上面所说的倾角的正弦比半径,且
比PG×4AT,亦即(因Pp比PG如同上面所说的倾角的正弦比半径,且
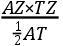 比4AT如同二倍的角ATn的正弦比四倍的半径)如同同一个倾角的正弦乘以二倍的交点离太阳的距离的正弦比四倍的半径的平方。
比4AT如同二倍的角ATn的正弦比四倍的半径)如同同一个倾角的正弦乘以二倍的交点离太阳的距离的正弦比四倍的半径的平方。
系理4 因为,当交点在方照时,倾角的小时变差(由本命题)比角33″.10.33iv如同IT×AZ×TG×[(Pp)/(PG)]比ATcub.,亦即,如同
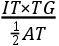 ×[(Pp)/(PG)]比2AT;这就是,如同月球离方照的距离的二倍的正弦乘以[(Pp)/(PG)]比二倍的半径;在交点的这一位置月球从方照移动到朔望期间(亦即,在17716小时的时间)的所有小时变差的和比同样数目的角33″.10.33iv之和,或者5878″,如同所有月球离方照的距离的二倍的正弦的和乘以[(Pp)/(PG)]比同样数目的直径的和;这就是,如同直径乘以(Pp)/(PG)比圆周;亦即,若倾角为5gr..1′,如同7×
×[(Pp)/(PG)]比2AT;这就是,如同月球离方照的距离的二倍的正弦乘以[(Pp)/(PG)]比二倍的半径;在交点的这一位置月球从方照移动到朔望期间(亦即,在17716小时的时间)的所有小时变差的和比同样数目的角33″.10.33iv之和,或者5878″,如同所有月球离方照的距离的二倍的正弦的和乘以[(Pp)/(PG)]比同样数目的直径的和;这就是,如同直径乘以(Pp)/(PG)比圆周;亦即,若倾角为5gr..1′,如同7×
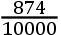 比22,或者278比10000。且因此,总的变差,它由所述期间所有小时变差的和凑成,为163″,或者2′.43″。
比22,或者278比10000。且因此,总的变差,它由所述期间所有小时变差的和凑成,为163″,或者2′.43″。
命题XXXV 问题XVI
给定时间,求月球的轨道对于黄道的平面的倾角。
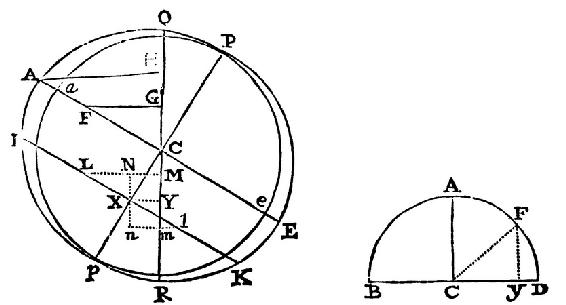
设AD为最大的倾角的正弦,且AB为最小的倾角的正弦。BD在C被平分,且以C为中心,BC为间隔画一个圆BGD。在AC上按照CE比EB之比与EB比2BA所具有的比相同,取CE;且对给定的时间,角AEG设为等于二倍的交点离方照的距离,并向AD落下垂线GH:则AH为寻求的倾角的正弦。

因为GEq等于GEq+HEq=BHD+HEq=HBD+HEq-BHq=HBD+BEq-2BH×BE=BEq+2EC×BH=2EC×AB+2EC×BH=2EC×AH。且因此,由于2EC被给定,GEq如同AH。现在指定AEg为某个给定的时间的瞬完成之后,交点离方照的距离的二倍,则弧Gg 由于角Geg被给定,如同距离GE。但是Hh比Gg 如同GH比GC,于是Hh如同容量GH×Gg,或者GH×GE;亦即,如同[(GH)/(GE)]×GEq或者[(GH)/(GE)]×AH,亦即,如同AH和角AEG的正弦的联合。所以,如果AH在任意一种情形是倾角的正弦,由上一命题的系理3,它将以相同的增量与倾角的正弦一起增大,且所以总与那个正弦保持相等。但AH,当点G无论落在点B或者点D时,等于这个正弦,且所以总保持与它相等。此即所证。

在这一证明中我曾假设角BEG,它是二倍的交点离方照的距离,均匀地增大。因为没有时间考虑均差的所有细节,现在设想角BEG为一直角,且在此情形Gg为二倍的交点和太阳彼此离开的距离的小时增加;且在同一情形倾角的小时变差(由上一命题的系理3)比33″.10.33iv如同倾角的正弦AH和直角BEG的正弦之下的容量,比四倍的半径的平方,BEG是二倍的交点离太阳的距离;亦即,如同平均倾角的正弦AH比四倍的半径;这就是(由于那个平均倾角约为5gr..
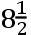 ′)如同其正弦896比四倍的半径40000,或者如同224比10000。且总的变差,与正弦的差BD对应,比那个小时变差,如同直径BD比弧Gg;亦即,如同直径BD比半圆周BGD和时间
′)如同其正弦896比四倍的半径40000,或者如同224比10000。且总的变差,与正弦的差BD对应,比那个小时变差,如同直径BD比弧Gg;亦即,如同直径BD比半圆周BGD和时间
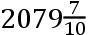 小时,在此期间交点自方照前进到朔望,比一小时的联合;这就是,如同7比22和
小时,在此期间交点自方照前进到朔望,比一小时的联合;这就是,如同7比22和
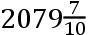 比1的联合。所以,如果所有的比联合起来,总的变差BD比33″.10.33iv如同224×7×
比1的联合。所以,如果所有的比联合起来,总的变差BD比33″.10.33iv如同224×7×
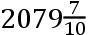 比110000,亦即,如同29645比1000,且因此得出那个变差BD为16′.
比110000,亦即,如同29645比1000,且因此得出那个变差BD为16′.
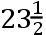 ″。
″。
这是不考虑月球在它自己的轨道上的位置时倾角的最大变差。因为倾角,如果交点在朔望,一点也不会由于月球的位置的不同而变化。但如果交点在方照,月球在朔望时的倾角小于月球在方照时的倾角,超出为2′.43″;正如我们在上一命题的系理四所指明的。且月球在方照,总的平均变差BD,减少这个超出的一半1′.
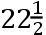 ″,变为15′.12″,但在朔望增大相同的量,变为17′.45″。所以,如果月球出现在朔望,总的变差在交点在从方照到朔望的路径上为17′.45″;且因此,如果倾角,当交点在朔望时,为5gr..17′.20″;则当交点在方照且月球在朔望时,为4gr..59′.35″。且这些结果已被观测证实。
″,变为15′.12″,但在朔望增大相同的量,变为17′.45″。所以,如果月球出现在朔望,总的变差在交点在从方照到朔望的路径上为17′.45″;且因此,如果倾角,当交点在朔望时,为5gr..17′.20″;则当交点在方照且月球在朔望时,为4gr..59′.35″。且这些结果已被观测证实。
如果现在需求当月球在朔望而交点在任意位置时轨道的倾角;设AB比AD如同4gr..59′.35″的正弦比5gr..17′.20″的正弦,并取角AEG等于二倍的交点离方照的距离:则AH是所寻求的倾角的正弦。当月球离交点90gr.远时,轨道的倾角等于这个倾角。在月球的其他位置,月均差,它从属于倾角的变化,在计算月球的纬度时以消除的方式为交点运动的月均差所平衡(如我们在以上所说),且因此在纬度的计算中可以被忽视。
解释
我期望由月球运动的这些计算证明,月球的运动能由重力的理论从它们的原因算出。由同一理论我更发现月球的平均运动的周年差(æquatio annua),按照第一卷命题LXVI系理6,起源于月球的轨道的倾角由于太阳的力发生的变化。当太阳在近地点,这个力较大,且扩大月球的轨道;在远地点它较小,且允许那个轨道收缩。在被扩大的轨道上月球运行得较缓慢,在被收缩的轨道上月球运行得较迅速;且周年差,由它这一不等性被补偿,在太阳的远地点和近地点消失,在太阳离地球的平均距离上大约升高到11′.50″,在其他位置与太阳的中心差成比例;且当地球自它的远日点向近日点前进中,它被加到月球的平均运动上,又在轨道的对面部分,它被从月球的平均运动中减去。假定地球的大轨道的半径为1000,且地球的偏心距为
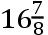 ,这个差,当它最大时,由重力理论得出为11′.49″。但地球的偏心率似乎略大;且如果偏心率增大这个差应按相同的比被增大。设偏心距为
,这个差,当它最大时,由重力理论得出为11′.49″。但地球的偏心率似乎略大;且如果偏心率增大这个差应按相同的比被增大。设偏心距为
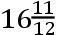 ,则最大的差为11′.51″。
,则最大的差为11′.51″。
我也发现,在地球的近日点,因为太阳的力较大,月球的远地点和交点比在地球的远日点运动得迅速,且按照地球离太阳的距离的三次反比。且由此引起这些运动的周年差与太阳的中心差成比例。但是,太阳的运动按照地球离太阳的距离的二次反比,且最大的中心差,它由这一不等性生成,是1gr..56′.20″,与前面所说太阳的偏心率
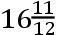 对应。且如果太阳的运动按照距离的三次反比,则由这一不等性生成的最大的[中心]差为2gr..54′.30″。且所以最大的差,它由月球的远地点和交点的运动的不等性生成,比2gr..54′.30″,如同月球的远地点的日平均运动和月球的交点的日平均运动比太阳的日平均运动。因此,得到远地点的平均运动的最大的差为19′.43″,且交点的平均运动的最大的差为9′.24″。当地球由其近日点向远日点前进时,加上前一个差且减去后一个差;又在轨道的相对的部分发生相反的情形。
对应。且如果太阳的运动按照距离的三次反比,则由这一不等性生成的最大的[中心]差为2gr..54′.30″。且所以最大的差,它由月球的远地点和交点的运动的不等性生成,比2gr..54′.30″,如同月球的远地点的日平均运动和月球的交点的日平均运动比太阳的日平均运动。因此,得到远地点的平均运动的最大的差为19′.43″,且交点的平均运动的最大的差为9′.24″。当地球由其近日点向远日点前进时,加上前一个差且减去后一个差;又在轨道的相对的部分发生相反的情形。
由重力理论亦可确立太阳对月球的作用,当月球的轨道的横截直径穿过太阳时比当这条直径与地球和太阳的连线成直角时稍大;且所以月球的轨道在前一种情形较后者稍大。且因此产生月球的平均运动的另一个差,它依赖月球的远地点对于太阳的位置;这个差当月球的远地点离太阳四十五度远时为最大;且当远地点抵达方照或者朔望时消失:在月球的远地点自太阳的方照到朔望的路径上它被加到平均运动上,且在月球的远地点自朔望到方照的路径中它被从平均运动中减去。这个差,我将称之为半年的,在远地点的八分点为最大,尽我能从天象推出的,约上升到3′.45″。这是在太阳离地球的平均距离时它的量。它按照太阳的距离的三次反比增大或者减小,因此在太阳的最大的距离很接近地为3′.34″,且在最小的距离很接近地为3′.56″;且当月球的远地点位于八分点之外时,它变得更小;且它比最大的差,如同月球的远地点离最近的朔望或者方照的距离的二倍的正弦比半径。
由同一重力理论,太阳对月球的作用当过月球的交点引的直线经过太阳时比当那条直线与太阳和地球的连线成直角时稍大。且因此产生月球平均运动的另一个差,我称之为第二半年差,且它当交点离太阳四十五度远时最大,且当交点在朔望和方照时消失,在交点的其他位置与交点离最近的朔望或者方照的距离的二倍的正弦成比例;如果太阳在离它最近的交点的前面,它被加到月球的平均运动,且如果太阳在后面,它被从月球的平均运动中减去;且在离太阳四十五度远,在那里它最大,在太阳离地球的平均距离,上升到47″,正如我由重力理论推得的。在太阳的其他距离,这个在离交点四十五度远时最大的差与太阳离地球的距离的立方成反比,且因此在太阳的近地点约上升到49″,在其远地点约上升到45″。
由同一重力理论,月球的远地点当它与太阳会合时或者相对时,它尽可能快地前进;当它相对于太阳在方照时,它后退。且由第I卷命题LXVI系理7、8和9,偏心率在前一种情形最大且在后一种情形最小。又由相同的系理,这些不等性极大,并生成远地点的主差,我称它是半年的。且最大的半年差,尽我能从天象推出的,约为12gr..18′。我们的同国人霍罗克斯,首先提出月球在围绕地球的一个椭圆上运动,地球位于其下焦点上。哈雷把椭圆的中心安置在一本轮(epicyclus)上,其中心均匀地围绕地球旋转。且由在旋轮线上的运动引起以上提到的在远地点的前行和后退以及在偏心率的量上的不等性。假设月球离地球的平均距离被分成100000份,并设T表示地球且TC表示5505份的月球的平均偏心距。延长TC至B,使得CB是最大的半年差12gr..18′对于半径TC的正弦,则以中心C,间隔CB画出的圆BDA是那个本轮,月球的轨道的中心被安置在其上并沿字母BDA的顺序旋转。取角BCD等于二倍的年角距(argumentum annum),或者二倍的太阳的真实位置离被一次取平后的月球的远地点的距离,则CTD为月球的远地点的半年差,而TD为其轨道的偏心率,趋向被二次取平后的远地点。但是,有了月球的平均运动和远地点以及偏心率,以及有200000份的轨道的长轴;由这些[数据]通过熟知的方法求得月球在其轨道上的真实位置和它离地球的距离。
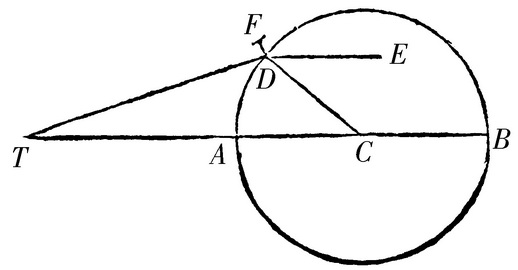
在地球的近日点,因为太阳的力较大,月球的轨道的中心围绕中心C比在远日点运动得更迅速,且这按照地球离太阳的距离的三次反比。由于太阳的中心差被包含在年角距中,月球的轨道的中心按照地球离太阳的距离的二次反比在本轮BDA上更迅速地运动。为使同一个中心按照距离的简单反比运动得更迅速;由轨道的中心D引一直线DE朝向月球的远地点,或者平行于直线TC;再取角EDF等于前面所说的年角距对月球的远地点沿向前的方向离太阳的近地点的距离的超出;或者这也得出同样的结果,取角CDF等于太阳的真近点角对360度的补角。又设DF比DC如同二倍的大轨道的偏心距比太阳离地球的平均距离和离开月球的远地点的太阳的日平均运动比离开它自己的远地点的太阳的日平均运动的联合,亦即,如同
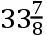 比1000和52′.27″.16比59′.8″.10的联合,或者如同3比100。再想象月球的轨道的中心位于点F,且在一中心为D,半径为DF的本轮上旋转,在此期间点D在圆DABD的周线上前进。因为按这种方式,月球的轨道的中心在围绕中心C画出的某一曲线上运动的速度,很近似地与太阳离地球的距离的立方成反比,正如它应当的。
比1000和52′.27″.16比59′.8″.10的联合,或者如同3比100。再想象月球的轨道的中心位于点F,且在一中心为D,半径为DF的本轮上旋转,在此期间点D在圆DABD的周线上前进。因为按这种方式,月球的轨道的中心在围绕中心C画出的某一曲线上运动的速度,很近似地与太阳离地球的距离的立方成反比,正如它应当的。
这一运动的计算是困难的,但可由以下的近似变得容易。如果设月球离地球的平均距离为100000份,且偏心距TC为5505,如同上面;直线CB或者CD被发现为
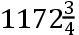 份,直线DF为
份,直线DF为
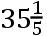 份。且这条直线[DF]在距离TC对着一个在地球的角,轨道的中心在这个中心的运动中自位置D到位置F的迁移中生成它;且同一直线的二倍在平行的位置以月球的轨道的上焦点离地球的距离,对着在地球的相同的角,在焦点的运动中生成那个迁移;且在月球离地球的距离它对着一个角,在月球的运动中生成相同的迁移,且所以可以称为第二中心差。再者,这个差,在月球离地球的平均距离,很接近地如同一个角的正弦,角由那条直线DF与自点F向月球所引的直线围成,且当它最大时为2′.25″。但直线DF和自F向月球所引的直线包含的角,或者通过从月球的平均近点角减去角EDF得到,或者通过月球的远地点离太阳的远地点的距离加上月球离太阳的距离得到。且由于半径比如此被发现的那个角的正弦,如同2′.25″比第二中心差。如果那个和小于半圆,第二中心差被加上;如果那个和大于半圆被减去。由此能够发现月球在[两个]发光体的朔望时它的经度。
份。且这条直线[DF]在距离TC对着一个在地球的角,轨道的中心在这个中心的运动中自位置D到位置F的迁移中生成它;且同一直线的二倍在平行的位置以月球的轨道的上焦点离地球的距离,对着在地球的相同的角,在焦点的运动中生成那个迁移;且在月球离地球的距离它对着一个角,在月球的运动中生成相同的迁移,且所以可以称为第二中心差。再者,这个差,在月球离地球的平均距离,很接近地如同一个角的正弦,角由那条直线DF与自点F向月球所引的直线围成,且当它最大时为2′.25″。但直线DF和自F向月球所引的直线包含的角,或者通过从月球的平均近点角减去角EDF得到,或者通过月球的远地点离太阳的远地点的距离加上月球离太阳的距离得到。且由于半径比如此被发现的那个角的正弦,如同2′.25″比第二中心差。如果那个和小于半圆,第二中心差被加上;如果那个和大于半圆被减去。由此能够发现月球在[两个]发光体的朔望时它的经度。
由于地球的大气直到35或者40哩的高度折射太阳光,通过折射,光线被散射到地球的阴影里,且由于光线在阴影边缘的散射扩大了阴影;对于阴影的直径,它由视差发现,在月食时我加上一分或者一分三十秒。
然而,月球的理论应由天象检查和证实,首先在朔望,其次在方照,而且最后在八分点。且任何着手完成这项工作的人在格林尼治皇家天文台用在旧历(55)(stilus vetus)1700年12月的最后一天的正午时太阳和月球的如下的平均运动,当不会不相宜,即,太阳的平均运动
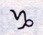 20gr..43′.40″,且其远地点的平均运动
20gr..43′.40″,且其远地点的平均运动
 7gr..44′.30″,又月球的平均运动
7gr..44′.30″,又月球的平均运动
 15gr..21′.00″,且其远地点的平均运动
15gr..21′.00″,且其远地点的平均运动
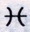 8gr..20′.00″,其升交点的平均运动
8gr..20′.00″,其升交点的平均运动
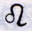 27gr..24′.20″,又这座天文台和巴黎皇家天文台的子午线的差为0hor..9min..20sec.(56);但月球的和其远地点的平均运动尚未充分精确地确定。
27gr..24′.20″,又这座天文台和巴黎皇家天文台的子午线的差为0hor..9min..20sec.(56);但月球的和其远地点的平均运动尚未充分精确地确定。
命题XXXVI 问题XVII
求移动海洋的太阳的力。
太阳的力ML或者PT,在月球的方照,对月球运动的摄动(由本卷命题XXV)比我们周围的重力,如同1比638092.6。且力TM-LM或者2PK在月球的朔望是[在方照时的]二倍。但是这些力,如果下降到地球的表面,它们按照离地球的中心的距离之比减小,亦即,按照
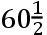 比1之比;且因此前一个力在地球的表面比重力如同1比38604600。由这个力海洋在一些地方受到压迫,那里离太阳90度远。另一个力,它有二倍大,不仅太阳下面的一片海洋而且对面的一片海洋也被它举起。这些力的和比重力如同1比12868200。且因为相同的力引起相同的运动,无论它压迫离太阳90度远的一片区域或者举起太阳之下以及太阳对面的一片海洋;这个和是太阳推动海洋的总力;且它有相同的作用,好像整个力举起在太阳之下的和太阳对面的区域的海洋,但在离太阳90度远的区域一点也没有作用。
比1之比;且因此前一个力在地球的表面比重力如同1比38604600。由这个力海洋在一些地方受到压迫,那里离太阳90度远。另一个力,它有二倍大,不仅太阳下面的一片海洋而且对面的一片海洋也被它举起。这些力的和比重力如同1比12868200。且因为相同的力引起相同的运动,无论它压迫离太阳90度远的一片区域或者举起太阳之下以及太阳对面的一片海洋;这个和是太阳推动海洋的总力;且它有相同的作用,好像整个力举起在太阳之下的和太阳对面的区域的海洋,但在离太阳90度远的区域一点也没有作用。
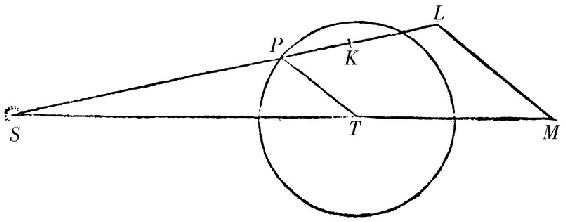
这是当太阳在任一给定位置的天顶点且在它自己离地球的平均距离上推动该处海洋的力。在太阳的其他位置,它举起海洋的力与太阳高出位置的地平线高度的二倍的正矢成正比,且与太阳离地球的距离的立方成反比。
系理 由于地球的部分的离心力,它起源于地球的周日运动,比重力如同1比289,它引起赤道之下的水的高度比两极之下的水的高度高出的尺寸为85472巴黎呎,如在前面的命题XIX所示;我们所论的太阳的力,由于它比重力如同1比12868200,因此比那个离心力如同289比12868200,或者1比44527,它引起太阳之下以及太阳对面区域的水比与离太阳90度远的地方的水高出的尺寸仅为一巴黎呎十一又三十分之一吋。因为该尺寸比85472这样的尺寸如同1比44527。
命题XXXVII 问题XVIII
求移动海洋的月球的力。
移动海洋的月球的力从它比太阳的力的比例推出,而这个比从海洋运动的比推出,它们起源于这些力。在[下]埃文河河口的前方,布里斯托尔下方第三块里程碑处,春季和秋季,在两个发光体(57)的合和冲,水的总的上升,根据撒母尔·斯图米的观测,约为45呎,但在方照时仅为25呎。前一个高度起源于力的和,后一个起于同样的力的差。所以,令太阳和月球在赤道且在离地球的平均距离的力为S和L,则L+S比L-S,如同45比25,或者9比5。
根据撒母尔·科尔普雷斯的观测,在普利茅斯港,海潮被举起的平均高度约为十六呎,但在春季和秋季,在朔望时海潮的高度能比在方照时的高度的超出多于七呎或者八呎。如果这些高度的最大的差是九呎,则L+S比L-S将如同
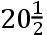 比
比
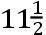 或者41比23。一个与前者足够符合的比。由于在布里斯托尔港的海潮的大小,斯图米的观测似乎更为可信,且因此在更确定的一些东西建立起来之前,我们使用9比5的比例。
或者41比23。一个与前者足够符合的比。由于在布里斯托尔港的海潮的大小,斯图米的观测似乎更为可信,且因此在更确定的一些东西建立起来之前,我们使用9比5的比例。
但是由于水的往复运动,最大的潮不发生在发光体的朔望,而在,如我们在前面所说,朔望后的第三次潮或者在朔望之后紧接着月球第三次靠近那个位置的子午线,或者更确定些(正如由斯图米注意到的)是朔月日或者望月日后的第三次潮;或者接近朔月或者望月之后的第十二小时,且因此大约发生在朔月或者望月之后的第四十三小时。但在这个港口它们大约发生在月球接近这个位置的子午线后的第七小时;且因此当月球离太阳的或者太阳的冲的距离,以向前的方向接近十八或者十九度时,它们紧跟在月球靠近子午线之后。在夏季和冬季,它们不是在二至点自身,而是当太阳离二至点约为整个圆的十分之一远时,或者约为36或者37度时,达到最大。且类似地,起源于月球靠近一个位置的最大的海潮,[发生在]月球离太阳约为从一次潮到下一次潮它的整个运动的十分之一远的时候。设那个距离约为
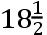 度。在月球离朔望和方照的这个距离上的太阳的力,对起源于月球的力的海洋的运动的增大和减小,按照半径比二倍的这个距离或者37度角的余弦,这就是,按照10000000比7986355的比小于在朔望和方照时它们自身。且因此在上面的类比中S应写成0.7986355S。
度。在月球离朔望和方照的这个距离上的太阳的力,对起源于月球的力的海洋的运动的增大和减小,按照半径比二倍的这个距离或者37度角的余弦,这就是,按照10000000比7986355的比小于在朔望和方照时它们自身。且因此在上面的类比中S应写成0.7986355S。
但是由于月球离开自赤道的倾角,在方照时月球的力应被减小。因为月球在方照,或者更确切些,在方照之后的
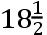 度,倾角约为22gr..13′。且自赤道倾斜的任一发光体移动海洋的力很接近地按照其倾角的余弦的二次比减小。且因此在这些方照月球的力仅为0.8570327L。所以L+0.7986355S比0.8570327L-0.7986355S如同9比5。
度,倾角约为22gr..13′。且自赤道倾斜的任一发光体移动海洋的力很接近地按照其倾角的余弦的二次比减小。且因此在这些方照月球的力仅为0.8570327L。所以L+0.7986355S比0.8570327L-0.7986355S如同9比5。
此外,月球应在其上无偏心地运动的轨道的直径,彼此如同69比70;且因此在朔望月球离地球的距离比在方照它离地球的距离如同69比70,若其他情况相同。且它的距离,当最大的潮生成时,离朔望
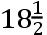 度,且当最小的潮生成时,离方照
度,且当最小的潮生成时,离方照
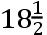 度,比它的平均的距离如同69.098747和69.897345比
度,比它的平均的距离如同69.098747和69.897345比
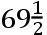 。但是移动海洋的月球的力按照距离的三次反比,且因此在这些最大的和最小的距离上的力比在平均的距离上的力如同0.9830427和1.017522比1。于是1.017522L+0.7986355S比0.9830427×0.8570327L-0.7986355S如同9比5。则S比L如同1比4.4815。所以,由于太阳的力比重力如同1比12868200,则月球的力比重力如同1比2871400。
。但是移动海洋的月球的力按照距离的三次反比,且因此在这些最大的和最小的距离上的力比在平均的距离上的力如同0.9830427和1.017522比1。于是1.017522L+0.7986355S比0.9830427×0.8570327L-0.7986355S如同9比5。则S比L如同1比4.4815。所以,由于太阳的力比重力如同1比12868200,则月球的力比重力如同1比2871400。
系理1 因为[海]水受太阳的力的作用升高至一呎十一又三十分之一吋的一个高度,受月球的力的作用它升高至八呎
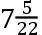 吋的一个高度,且两力的作用使海水升高至十又二分之一呎,又当月球在近地点会使水升高到十二又二分之一呎或者更高的一个高度,特别是在风助海潮的时候。如此大的一个力引起海洋的所有运动是绰绰有余的,且恰与诸运动的量对应。因为在海洋,它们自东往西广袤地延伸,如在太平洋,以及在大西洋和埃塞俄比亚海(58)(Mare Æthiopicum)的回归线之外的部分,水通常被举起到六、九、十二或者十五呎的一个高度。但在太平洋,它更深且更宽广,海潮据说比在大西洋和埃塞俄比亚海的海潮大。因为为了有一个全潮,海洋自东往西的宽度应不小于九十度。在埃塞俄比亚海,因为此海在非洲和美洲南部之间的狭窄,海水在回归线之间的升高小于在温带的升高。在海洋的中间,水不能上升,除非在东海岸和西海岸的水同时下降;然而,在我们的狭窄的海洋,水应在那些海岸交替下降。由于这个原因,在海岛上的涨潮和落潮,它们离海岸极远,通常甚小。在某些港口,那里水以大的冲击通过浅的地方流入并流出,交替地填满并清空海湾,涨潮和落潮必较通常要大,如在英吉利的普利茅斯和切普斯托桥,在诺曼底的圣米歇尔山和阿布瑞卡图奥勒姆镇(通称阿夫朗什);在东印度的坎贝和勃固。在这些地方,海水以大的速度到来和退去,有时淹没海岸,有时留下许多哩的干燥海岸。且流入的和回流的冲击在水被举起或者压下至30、40或者50呎以及更高之前,不会被削弱。且这个理由亦适于长而浅的海峡,如麦哲伦海峡和那些环绕英吉利的海峡。海潮在此类港口和海峡中由于水流入和流出的冲击而极度增大。但在海岸,它们以陡坡面对深而且开阔的海洋,水没有流入和回流的冲击亦能被举起并降低,海潮的大小对应于太阳和月球的力。
吋的一个高度,且两力的作用使海水升高至十又二分之一呎,又当月球在近地点会使水升高到十二又二分之一呎或者更高的一个高度,特别是在风助海潮的时候。如此大的一个力引起海洋的所有运动是绰绰有余的,且恰与诸运动的量对应。因为在海洋,它们自东往西广袤地延伸,如在太平洋,以及在大西洋和埃塞俄比亚海(58)(Mare Æthiopicum)的回归线之外的部分,水通常被举起到六、九、十二或者十五呎的一个高度。但在太平洋,它更深且更宽广,海潮据说比在大西洋和埃塞俄比亚海的海潮大。因为为了有一个全潮,海洋自东往西的宽度应不小于九十度。在埃塞俄比亚海,因为此海在非洲和美洲南部之间的狭窄,海水在回归线之间的升高小于在温带的升高。在海洋的中间,水不能上升,除非在东海岸和西海岸的水同时下降;然而,在我们的狭窄的海洋,水应在那些海岸交替下降。由于这个原因,在海岛上的涨潮和落潮,它们离海岸极远,通常甚小。在某些港口,那里水以大的冲击通过浅的地方流入并流出,交替地填满并清空海湾,涨潮和落潮必较通常要大,如在英吉利的普利茅斯和切普斯托桥,在诺曼底的圣米歇尔山和阿布瑞卡图奥勒姆镇(通称阿夫朗什);在东印度的坎贝和勃固。在这些地方,海水以大的速度到来和退去,有时淹没海岸,有时留下许多哩的干燥海岸。且流入的和回流的冲击在水被举起或者压下至30、40或者50呎以及更高之前,不会被削弱。且这个理由亦适于长而浅的海峡,如麦哲伦海峡和那些环绕英吉利的海峡。海潮在此类港口和海峡中由于水流入和流出的冲击而极度增大。但在海岸,它们以陡坡面对深而且开阔的海洋,水没有流入和回流的冲击亦能被举起并降低,海潮的大小对应于太阳和月球的力。
系理2 由于月球移动海洋的力比重力如同1比2817400,显然那个力比用摆的实验,或者任何静力学或者流体静力学中的实验所能察觉到的力要小很多。只在海洋的潮汐中,这个力才产生显著效应。
系理3 因为月球移动海洋的力比太阳的同类的力如同4.4815比1,且那些力(由第I卷命题LXIV系理14)如同月球和太阳的本体的密度及它们的视直径的立方的联合;月球的密度比太阳的密度如同4.4815比1的正比,和月球的直径的立方比太阳的直径的立方的反比,亦即如同4891比1000。(因为月球的和太阳的平均视直径为31′.
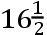 ″和32′.12″)但是,太阳的密度比地球的密度如同1000比4000;且因此月球的密度(59)比地球的密度如同4891比4000,或者11比9。所以月球的本体比我们的地球更致密且有更多的土壤。
″和32′.12″)但是,太阳的密度比地球的密度如同1000比4000;且因此月球的密度(59)比地球的密度如同4891比4000,或者11比9。所以月球的本体比我们的地球更致密且有更多的土壤。
系理4 且因为由天文观测,月球的真实直径比地球的真实直径如同100比365;月球的质量与地球的质量如同1比39.788。
系理5 且在月球表面的加速重力约比地球表面的加速重力小三倍。
系理6 且月球中心离地球中心的距离比月球中心离地球和月球的重力的公共中心的距离,如同40.788比39.788。
系理7 且在月球的八分点,月球中心离地球中心的平均距离很接近
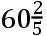 个地球的最大的半直径。因为地球的最大的半直径为19658600巴黎呎,则地球和月球的中心之间的平均距离由
个地球的最大的半直径。因为地球的最大的半直径为19658600巴黎呎,则地球和月球的中心之间的平均距离由
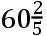 个这样的半直径构成,等于1187379440呎。且这个距离(由上一系理)比月球中心离地球和月球的重力的公共的中心的距离,如同40.788比39.788:且因此后一距离为1158268534呎。又由于月球相对于恒星的运行为27天7小时又
个这样的半直径构成,等于1187379440呎。且这个距离(由上一系理)比月球中心离地球和月球的重力的公共的中心的距离,如同40.788比39.788:且因此后一距离为1158268534呎。又由于月球相对于恒星的运行为27天7小时又
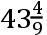 分钟;一个角的正矢,这个角由月球在一分钟的时间画出,为12752341,半径取为1000000000000000。且由于此半径比这个正矢,如同1158268534呎比14.7706353呎。所以月球以那个力,由那个力月球被保持在轨道上,向地球下落,一分钟的时间画出14.7706353呎。又按照
分钟;一个角的正矢,这个角由月球在一分钟的时间画出,为12752341,半径取为1000000000000000。且由于此半径比这个正矢,如同1158268534呎比14.7706353呎。所以月球以那个力,由那个力月球被保持在轨道上,向地球下落,一分钟的时间画出14.7706353呎。又按照
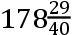 比
比
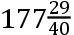 之比增加这个力,由命题III的系理,得到在月球轨道上总的重力。月球又由这个力向地球下落,在一分钟的时间它画出14.8538067呎。且在六十分之一个月球离地球的中心的距离,亦即在离地球的中心197896573呎的一段距离,重物下落,在一秒钟的时间也画出14.8538067呎。且因此在[离地球的中心]19615800呎的一段距离,这段距离是地球的平均的半直径,重物下落[在一秒钟的时间]画出15.11175呎,或者15呎1吋又
之比增加这个力,由命题III的系理,得到在月球轨道上总的重力。月球又由这个力向地球下落,在一分钟的时间它画出14.8538067呎。且在六十分之一个月球离地球的中心的距离,亦即在离地球的中心197896573呎的一段距离,重物下落,在一秒钟的时间也画出14.8538067呎。且因此在[离地球的中心]19615800呎的一段距离,这段距离是地球的平均的半直径,重物下落[在一秒钟的时间]画出15.11175呎,或者15呎1吋又
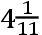 吩。这是物体在45度的纬线上的下落。且由前面画在命题XX中的一张表,下落稍大于在巴黎的纬度的下落,超出约为
吩。这是物体在45度的纬线上的下落。且由前面画在命题XX中的一张表,下落稍大于在巴黎的纬度的下落,超出约为
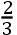 吩。所以,由这一计算,在巴黎的纬度重物在真空中下落,在一秒钟的时间约画出15巴黎呎1吋又
吩。所以,由这一计算,在巴黎的纬度重物在真空中下落,在一秒钟的时间约画出15巴黎呎1吋又
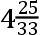 吩。且如果重力除去离心力而被减小,离心力起源于在那个纬度的地球的周日运动;重物在那里下落,一秒钟的时间画出15呎1吋又
吩。且如果重力除去离心力而被减小,离心力起源于在那个纬度的地球的周日运动;重物在那里下落,一秒钟的时间画出15呎1吋又
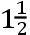 吩。且在上面的命题IV和XIX中已经证明,重物以这个速度在巴黎的纬度下落。
吩。且在上面的命题IV和XIX中已经证明,重物以这个速度在巴黎的纬度下落。
系理8 地球和月球的中心之间的平均距离在月球的朔望,是60个地球的最大的半直径除去大约
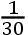 个地球的最大的半直径。且在月球的方照,相同的中心之间的平均距离是
个地球的最大的半直径。且在月球的方照,相同的中心之间的平均距离是
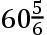 个地球的半直径。因为由命题XXVIII这两个距离比月球在八分点的平均距离如同69和70比
个地球的半直径。因为由命题XXVIII这两个距离比月球在八分点的平均距离如同69和70比
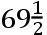 。
。
系理9 地球的和月球的中心之间的平均距离在月球的朔望是六十又十分之一个地球的平均的半直径。且在月球的方照,相同的中心之间的平均距离,去掉三十分之一个半直径,是六十一个地球的平均的半直径。
系理10 在月球的朔望,其平均的地平视差在0,30,38,45,52,60,90度的纬度上,分别为57′.20″,57′.16″,57′.14″,57′.12″,57′.10″,57′.8″和57′.4″。
在这些计算中,我没有考虑地球的磁吸引,其量太小且未知。但是如果几时能定出这一吸引,且如果在子午线度数的测量,在不同的纬线上等时的摆的长度,海洋运动的定律和月球的视差以及太阳和月球的视直径几时能从天象更精确地确定;那时可使这一计算更为精确。
命题XXXVIII 问题XIX
求月球的本体的形状。
如果月球的本体是像我们的海洋那样的流体,举起那一流体的最近的和最远的部分的地球的力,比月球的力,由月球的力我们的大海在月球下方的和月球对面的部分被举起,如同月球向着地球的重力加速度比地球对月球的重力加速度,以及月球的直径比地球的直径的联合;亦即,如同39.788比1和100比365的联合,或者如同1081比100。因此,由于我们的海洋被月球的力举起到
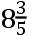 呎,地球的力应把月球的流体举起到93呎。且由于这个原因月球的形状是一个扁球,它的最大的直径延长穿过地球中心,且超出垂直于它的直径186呎。所以,如此的形状是月球现在具有的,而且是从一开始就必定具有的。此即所求。
呎,地球的力应把月球的流体举起到93呎。且由于这个原因月球的形状是一个扁球,它的最大的直径延长穿过地球中心,且超出垂直于它的直径186呎。所以,如此的形状是月球现在具有的,而且是从一开始就必定具有的。此即所求。
系理 由此月球恒以它的相同的一个面转向地球。因为在其他任意位置,月球的本体不能静止,而经振动它总返回到这个位置。然而振动极为缓慢,由于产生它们的力极小;因此使得那个面,它应总是转向地球,能转向(由在命题XXVII中给出的理由)月球轨道的另一个焦点,且不从那里马上被拉回并向地球旋转。
引理 I
如果指定APEp为密度均匀的地球,且用中心C,两极P和p,以及赤道AE描绘;并假设以中心C,半径CP画出一个球Pape;设QR为一个平面,从太阳的中心向地球的中心所引的直线以九十度的角立在它上面。又若地球的整个靠外的部分PapAPepE,它高于刚刚画出的球,它的每个小部分努力在两个方向上退离平面QR,且每个小部分退离的努力如同它离平面的距离:我说,首先,在赤道的圆AE上的所有小部分,它们均匀地分布在球外,按环的方式整个地围绕这个球,使地球围绕其中心旋转的力和作用,比放在赤道上点A的同样数目的小部分,这个点离平面QR最远,使地球围绕其中心做类似的圆运动的力和作用,如同一比二。并且那个圆运动围绕位于赤道和平面QR的共同部分的轴进行。
设以中心K,直径IL画出半圆INLK。假设半圆周INL被分成无数相等的部分,且自每一部分N向直径IL落下正弦[线]NM。则所有正弦NM的平方的和等于正弦KM的平方的和,且两者的和等于同样数目的半直径KN的平方的和;且因此所有NM的平方的和是同样数目的半直径KN的平方的和的一半。
现在圆AE的周线被分成相同数目的相等的小部分,且从每个这样的小部分F向平面QR落下垂线FG,又从点A落下垂线AH。且力,由它小部分F退离平面QR,由假设如同那条垂线FG,且这个力乘以距离CG 是小部分F使地球围绕其中心转动的作用。且因此,在位置F的小部分的作用,比在位置A的小部分的作用,如同FG×GC比AH×HC,这就是,如同FCq比ACq;于是在自己位置的所有小部分F的总的作用比在位置A的同样数目的小部分的作用,如同所有的FCq的和比同样数目的ACq的和,这就是(由已证明的)如同一比二。此即所证。
且由于小部分通过垂直地退离平面QR而发生作用,因此对于这个平面的每一侧是相等的:围绕既位于那个平面QR又位于赤道的平面的轴,它们旋转赤道的圆的周线,以及附着于它的地球。
引理 II
在同样的条件下:我说,其次,位于球外各处的所有小部分的使地球围绕同一轴旋转的总的力和作用,比同样数目的小部分的总的力,这些小部分按照环的方式均匀地分布在赤道的圆AE上,使地球做类似的圆运动,如同二比五。
因为,设IK为平行于赤道AE的任意一个较小的圆,又设L,l为在这个圆上位于球Pape外的任意两个相等的小部分。如果向平面QR上,该平面垂直于向太阳引的半径,落下垂线LM,lm:总的力,由它们那些小部分逃离平面QR,与那些垂线LM,lm成比例。再设直线Ll平行于平面Pape且在X被平分,又过点X引Nn,它平行于平面QR并且交垂线LM,lm于N和n,又在平面QR上落下垂线XY。则小部分L和l在相反的方向转动地球的相反的力,如同LM×MC和lm×mC,这就是,如同LN×MC+NM×MC和ln×mC-nm×mC,或者LN×MC+NM×MC和LN×mC-NM×mC;且它们的差LN×Mm-NM×
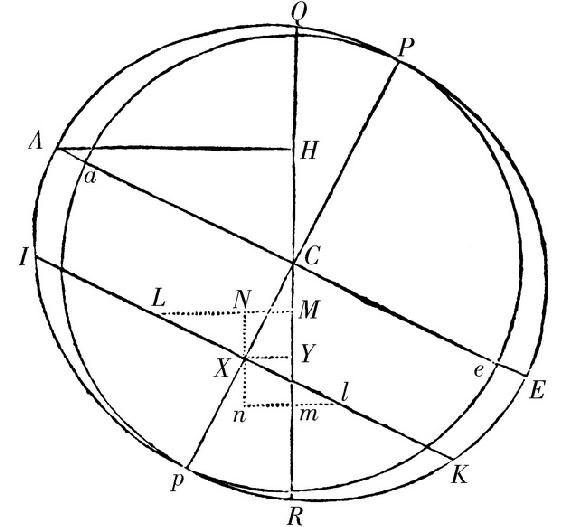
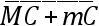 是两个小部分合并转动地球的力。这个差的正的部分LN×Mm或者2LN×NX比位于A的相同大小的两个小部分的力2AH×HC,如同LXq比ACq。且负的部分NM×
是两个小部分合并转动地球的力。这个差的正的部分LN×Mm或者2LN×NX比位于A的相同大小的两个小部分的力2AH×HC,如同LXq比ACq。且负的部分NM×
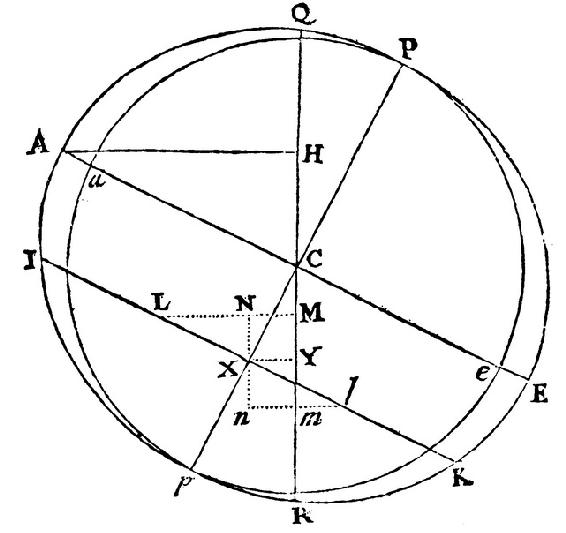
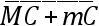 或者2XY×CY比位于A的相同的两个小部分的力2AH×HC,如同CXq比ACq。所以部分的差,亦即,两个小部分L和l合并转动地球的力比两个小部分的力,它们有相同的大小且处于位置A并类似地转动地球,如同LXq-CXq比ACq。但是,如果圆IK的周线IK被分成无数相等的小部分L,(由引理I)所有的LXq比同样数目的IXq,如同1比2,且因此比同样数目的ACq,如同IXq比2ACq;且同样数目的CXq比同样数目的ACq,如同2CXq比2ACq。所以在圆IK的周线上的小部分联合起来的力比相同数目的小部分在位置A联合起来的力,如同IXq-2CXq比2ACq;且所以(由引理I)比在圆AE的周线上的同样数目的小部分联合起来的力,如同IXq-2CXq比ACq。
或者2XY×CY比位于A的相同的两个小部分的力2AH×HC,如同CXq比ACq。所以部分的差,亦即,两个小部分L和l合并转动地球的力比两个小部分的力,它们有相同的大小且处于位置A并类似地转动地球,如同LXq-CXq比ACq。但是,如果圆IK的周线IK被分成无数相等的小部分L,(由引理I)所有的LXq比同样数目的IXq,如同1比2,且因此比同样数目的ACq,如同IXq比2ACq;且同样数目的CXq比同样数目的ACq,如同2CXq比2ACq。所以在圆IK的周线上的小部分联合起来的力比相同数目的小部分在位置A联合起来的力,如同IXq-2CXq比2ACq;且所以(由引理I)比在圆AE的周线上的同样数目的小部分联合起来的力,如同IXq-2CXq比ACq。
现在,如果球的直径Pp被分成无数相等的小部分,在其上直立着同样数目的圆IK;在每一个圆IK的周线上的物质如同IXq:且因此那些物质转动地球的力,如同IXq乘以IXq-2CXq。且相同的物质的力,如果它们在圆AE的周线上,如同IXq乘以ACq。且所以,全部物质的所有小部分的力,它们位于球之外的所有的圆的周线上,比位于最大的圆AE的周线上的同样数目的小部分的力,如同所有的IXq乘以IXq-2CXq比同样数目的IXq乘以ACq,这就是,如同所有的ACq-CXq乘以ACq-3CXq比同样数目的ACq-CXq乘以ACq,亦即,如同所有的ACqq-4ACq×CXq+3CXqq比同样数目的ACqq-ACq×CXq,这就是,如同整个流量,其流数为ACqq-4ACq×CXq+3CXqq,比整个流量,其流数为ACqq-ACq×CXq;且因此,由流数方法,如同ACqq×CX-
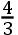 ACq×CXcub.+
ACq×CXcub.+
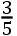 CXqc比ACqq×CX-
CXqc比ACqq×CX-
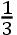 ACq×CXcub.,亦即,如果CX代之以整个Cp或者AC,如同
ACq×CXcub.,亦即,如果CX代之以整个Cp或者AC,如同
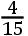 ACqc比
ACqc比
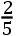 ACqc,这就是,如同二比五。此即所证。
ACqc,这就是,如同二比五。此即所证。
引理 III
在同样的条件下:我说,其三,整个地球围绕以上描述过的轴的运动,该运动由所有小部分的运动组成,比以上所说的围绕相同的轴的环的运动按照一个比,该比由来自在地球中的物质比在环中的物质之比,以及任意一个圆的四分之一弧的平方的三倍比直径的平方的二倍之比复合而成;亦即,按照物质比物质以及数925275比数1000000之比。
因为,圆柱围绕其不动的轴旋转的运动比与它一起旋转的内切球的运动,如同任意四个相等的正方形比三个内切于它们的圆;且圆柱的运动比一个极薄的环的运动,它在球和圆柱共同接触的地方环绕它们,如同二倍的在圆柱中的质量比三倍的在环中的质量;且环的这个围绕圆柱的轴均匀地持续的运动,比环围绕它自身的直径的均匀运动,这些运动在相同的循环时间完成,如同一个圆的圆周比二倍的它的直径。
假设 II
如果上述的环,地球的其余所有部分被除去,单独地在地球的轨道上以周年运动围绕太阳旋转,且在此期间围绕其轴,它以
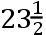 度的角向黄道的平面倾斜,以周日转动旋转:二分点的运动是相同的,无论环是流体的或者是由刚性且牢固的物质组成。
度的角向黄道的平面倾斜,以周日转动旋转:二分点的运动是相同的,无论环是流体的或者是由刚性且牢固的物质组成。
命题XXXIX 问题XX
求岁差。
在圆轨道上月球的交点的平均小时运动,当交点在方照时,是16″.35.16iv.36v,且它的一半8″.17.38iv.18v(由于以上解释的理由)是交点在这样的一条轨道上的小时平均运动;且在整整一个恒星年达到20gr..11′.46″。所以,因为在这样的一条轨道上,月球的交点在一年后退20gr..11′.46″;且如果有多个月球,每个交点的运动(由第I卷命题LXIV系理16)将如同它的循环时间;如果月球在一个恒星日的时间靠近地球的表面运行,交点的年运动比20gr..11′.46″如同一个恒星日的23小时56′比月球的循环时间27天7小时43′,亦即,如同1436比39943。且对环绕地球的诸月球的环的交点,无论那些月球相互不接触,或者变成流体并形成一个连续的环,或者最后那个环冻结并变成刚性不变形的环,结果是一样的。
所以,我们设想这个环,它的物质的量等于球Pape外面地球所有的部分PapAPepE(参见边码473页上的图);且因为这个球比靠外的地球的那个部分,如同aCqu.比ACqu.-aCqu.,亦即(由于地球的短半直径PC或者aC比长半直径AC如同229比230)如同53441比459;如果这个环沿赤道缠绕且两者一起围绕环的直径旋转,环的运动比里面球的运动(由本卷的引理III)如同459比52441和1000000比925275的联合,这就是,如同4590比485223;且因此,环的运动比环的和球的运动的和,如同4590比489813。因此,如果环附着在球上,且其自身的运动,由它其交点或者二分点退行,传递给球;在环上尚存的运动比它原来的运动,如同4590比489813;于是二分点的运动按相同的比减小。所以,由环和球构成的物体的二分点的年运动比运动20gr..11′.46″,如同1436比39343和4590比489813的联合,亦即,如同100比292369。但是,力,由它月球的交点(正如我在上面所解释的)退行,且因此由它环的二分点退行(亦即在边码539和540页上的力3IT),在每一小部分如同那个小部分离平面QR的距离,且小部分以这些力逃离那个平面;且所以(由定律II)如果环的物质散布到球的整个表面,按照图形PapAPepE的样式构成地球的外面部分,所有的小部分使地球围绕它的赤道的任意直径旋转的力和作用,且因此使二分点运动,将按照2比5的比较以前变小。则由此现在周年岁差比20gr..11′.46″如同10比73092;且因此它成为9″.56.50iv。
但是,由于赤道的平面对黄道的平面的倾斜,这个运动按照正弦91706(它是
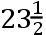 度的余角的正弦)比半径100000之比减小。这个运动现在变成9″..7′″.20iv。这是起源于太阳的力的周年岁差。
度的余角的正弦)比半径100000之比减小。这个运动现在变成9″..7′″.20iv。这是起源于太阳的力的周年岁差。
但是月球移动大海的力比太阳的力约略如同4.4815比1。且月球移动二分点的力比太阳的力按照相同的比。且因此得出起源于月球的力的周年岁差是40″..52.52iv,而起源于两者的力的整个周年岁差为50″..00.12iv。且这一运动与天象相符。因为由天文观测,每年的岁差在五十秒左右。
如果地球在赤道的高度超出在两极的高度
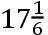 哩,其物质在边界上比在中心稀薄;岁差应由于高度的超出而增大,且由于较大的稀薄度而减小。
哩,其物质在边界上比在中心稀薄;岁差应由于高度的超出而增大,且由于较大的稀薄度而减小。
现在,我们已描述了太阳、地球、月球和诸行星的系统;余下的应加入论彗星的一些内容。
引理 IV
诸彗星高于月球并位于行星的区域内。
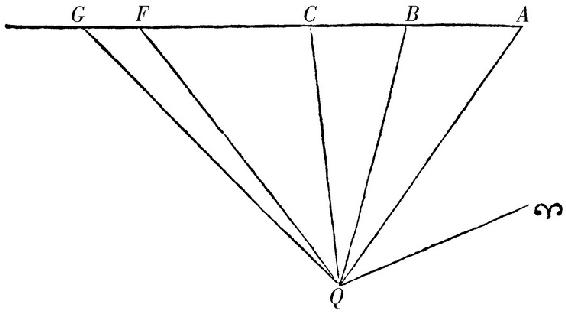
由于缺乏周日视差,彗星被抬高到月球以下区域的上方,因此它们的周年视差是它们升入行星区域的令人信服的证据。因为彗星,它们按[黄道十二]宫的顺序前进,如果地球在它们和太阳之间,全都在快不可见时比通常缓慢或者退行;如果地球靠近对面,它们比通常更迅速。且反之,当那些彗星逆着[黄道十二]宫的顺序前进时,如果地球在它们和太阳之间,在快不可见时比它们应当要迅速;且如果地球位于太阳的另一侧,它们以比它们应当的速度缓慢或者退行。这主要由于地球在其不同的位置上的运动,正如对于行星的情形,它根据与地球的运动一致或者相反,有时退行,有时看起来前进得缓慢,有时迅速。如果地球与一颗彗星在相同的方向前进,且绕太阳的角运动如此迅速,使得持续通过地球和彗星引的直线汇聚于彗星之外的区域,从地球上观察彗星,由于它们自身运动的缓慢而表现为退行;如果地球缓慢移动,彗星的运动(除去地球的运动)最少也变得更慢。但如果地球在彗星运动的相反方向前进,于是彗星看起来更迅速。按如下方式从加速或者迟滞或者退行运动可推知彗星的距离。令
 QA,
QA,
 QB,
QB,
 QC是在运动开始时三次观测到的彗星的黄经,且
QC是在运动开始时三次观测到的彗星的黄经,且
 QF为最后一次观测到的黄经,当时彗星刚要看不见。引直线ABC,其部分AB,BC位于直线QA和QB,QB和QC之间,且彼此如同前三次观测之间的时间。延长AC至G,使得AG比AB如同初次和最后一次观测之间的时间比初次和第二次观测之间的时间,并连结QG。则如果彗星沿直线均匀地运动,又地球或者静止,或者也在直线上以均匀的运动前进,角
QF为最后一次观测到的黄经,当时彗星刚要看不见。引直线ABC,其部分AB,BC位于直线QA和QB,QB和QC之间,且彼此如同前三次观测之间的时间。延长AC至G,使得AG比AB如同初次和最后一次观测之间的时间比初次和第二次观测之间的时间,并连结QG。则如果彗星沿直线均匀地运动,又地球或者静止,或者也在直线上以均匀的运动前进,角
 QG将为最后一次时间观测到的彗星的黄经。所以角FQG,它是黄经的差,起源于彗星的和地球的运动的不等性。但是这个角,如果地球和彗星在相反的方向上运动,应加到角
QG将为最后一次时间观测到的彗星的黄经。所以角FQG,它是黄经的差,起源于彗星的和地球的运动的不等性。但是这个角,如果地球和彗星在相反的方向上运动,应加到角
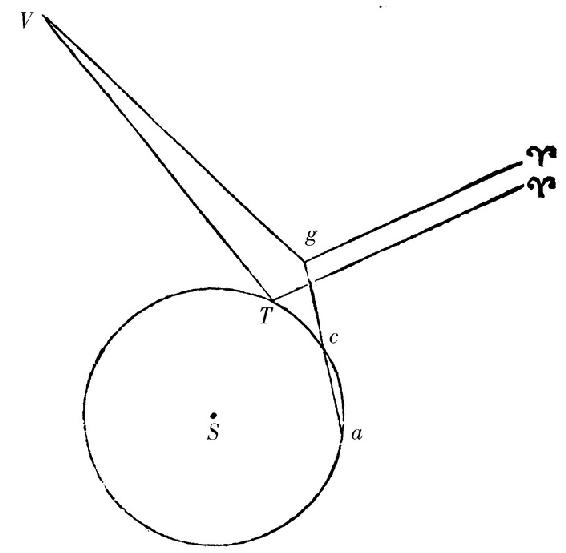
 QG上,且由此使彗星的视运动加快;否则,如果彗星在与地球相同的方向上前进,这个角被从同一个角中减去,而使彗星的运动或者变慢,或者可能退行;正如我刚才解释过的。所以这个角度主要起源于地球的运动,且因此作为彗星的视差是适当的,自然,它的某些增量或者减量被忽视了,它们可能起源于彗星在它自己轨道上运动的不等性。彗星的距离可由这个视差如此推得。指定S为太阳,acT为大轨道,a为在初次观测时地球的位置,c为在第三次观测时地球的位置,T为在最后一次观测时地球的位置,且T
QG上,且由此使彗星的视运动加快;否则,如果彗星在与地球相同的方向上前进,这个角被从同一个角中减去,而使彗星的运动或者变慢,或者可能退行;正如我刚才解释过的。所以这个角度主要起源于地球的运动,且因此作为彗星的视差是适当的,自然,它的某些增量或者减量被忽视了,它们可能起源于彗星在它自己轨道上运动的不等性。彗星的距离可由这个视差如此推得。指定S为太阳,acT为大轨道,a为在初次观测时地球的位置,c为在第三次观测时地球的位置,T为在最后一次观测时地球的位置,且T
 为向白羊宫的开始处引的直线。取角
为向白羊宫的开始处引的直线。取角
 TV等于角
TV等于角
 QF,这就是,等于当地球位于T时彗星的黄经。连结ac,并延长它至g,使得ag 比ac如同AG比AC,则g是一个位置,若地球在直线ac上均匀地持续,在最后一次观测的时间碰到它。且因此,如果引g
QF,这就是,等于当地球位于T时彗星的黄经。连结ac,并延长它至g,使得ag 比ac如同AG比AC,则g是一个位置,若地球在直线ac上均匀地持续,在最后一次观测的时间碰到它。且因此,如果引g
 平行于T
平行于T
 ,并取角
,并取角
 gV等于角
gV等于角
 QG,则这个角
QG,则这个角
 gV 等于自位置g观察时彗星的黄经;且角TVg为视差,它起源于地球自位置g到位置T的迁移;且因此V是在黄道的平面上彗星的位置。但是这个位置V一般低于木星的轨道。
gV 等于自位置g观察时彗星的黄经;且角TVg为视差,它起源于地球自位置g到位置T的迁移;且因此V是在黄道的平面上彗星的位置。但是这个位置V一般低于木星的轨道。
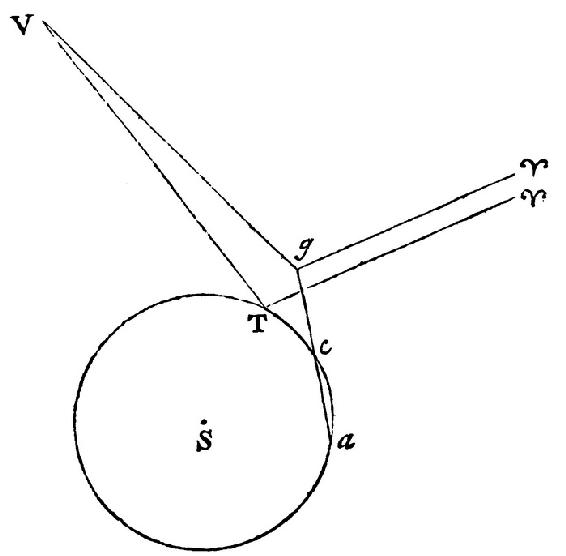
由彗星的路径的曲率可以推断出同样的事情。这些物体当它们运动得更迅速时几乎在极大的圆上前进;但在它们的路径的结束,当物体的视运动的那个部分,它起源于视差,比整个视运动有较大的比时,它们通常从这些圆偏离,且每次当地球在一个方向运动时,它们在相反的方向消失。这种偏离主要起源于视差,所以它与地球的运动对应;且其显著的量,根据我的计算,推断出彗星消失的位置远在木星之下。因此,结果是当彗星在它们的近地点和近日点更靠近我们时,经常降到火星以及更靠下的行星的轨道之下。
彗星的靠近也可从[它们的]头部的光得以证实。因为被太阳照耀且向更遥远的区域离去的天体,其光辉按照距离的四次比减小;显然由于物体离太阳的距离的增大它按照一个二次比减小,且由于视直径的减小它按照另一个二次比减小。因此如果彗星的光的量和视直径被给定,则按照彗星的直径比一个行星的直径的正比和彗星的光比行星的光的二分之一次反比,取彗星的距离比行星的距离,彗星的距离被给定。于是1682年的彗星(60)的彗发的最小直径,按弗拉姆斯蒂德用带测微计的十六呎长的望远镜的观测,等于2′.0″;但在彗发中间的彗核或者星占据这个宽度的不及十分之一,且因此仅宽8″或者12″。但是头部的光和明亮超过1680年的彗星(61)的头部,且与一等或者二等星取齐。我们假设土星及其环约为四倍亮,且因为环的光几乎等于它里面的球的光,又球的视直径约为21″,且因此球和环的光联合起来等于一个球的光,其直径为30″;彗星的距离比木星的距离如同1比√4的反比和12″比30″的正比,亦即,如同24比30或者4比5。再者,1665年4月的彗星,按赫维留的报告,其明亮几乎超过所有的恒星,且甚至超过土星自身,理由是其远为鲜亮的颜色。的确,这颗比另一颗明亮,后者在上一年的年未出现且堪与一等星相比。彗星的彗发的宽度约为6′,但核与行星相比,借助望远镜,它无疑小于木星,且被断定为有时小于土星的中间的物体,有时等于它。然而,由于彗星的彗发很少超过8′或者12′,彗核的,或者中心的星的直径约为彗发直径的约十分之一或者也许为十五分之一,显然这些星大多有与行星相同的视星等。因此,由于它们的光堪与土星的光相比并不罕见,且有时超过它;很清楚,所有的彗星在它们的近日点被安置得或者低于土星,或者高于它不远。所以使彗星远去到几乎是恒星的区域的人是完全错误的;无疑在这种情形,它们受到我们的太阳的照耀,它们在我们这里不会比行星受到恒星的照耀更多。
在我们讨论这些事情时,没有考虑彗星由于那种极多且浓的烟而出现的模糊,它包围彗星的头,仿佛彗星的头总是通过云而暗淡地发光。因为一个物体被这种烟模糊得愈甚,它必须愈靠近太阳,使得被它反射的大量的光可与行星的光相媲。因此彗星可能下降得远低于土星的球,正如我们由它们的视差所证明的。尤其是由彗尾能证实同样的事情。这些或者起源于被散布于以太中的烟所反射的光,或者起源于彗星头的光。在前一种情形彗星的距离必须被减小,否则总是起源于彗星的头的烟以难以置信的速度和扩展在巨大的空间传播。在后一种情形,彗尾的和彗星的头的所有的光必须归之于彗星的头的核。所以,如果我们假设所有这些光联合并聚积在彗核的圆盘(discus)内,则无疑那个核,当它发出极大和极亮的尾时,它的明亮远超木星。所以,如果它有一个较小的视直径并发出更多的光,它将更多地被太阳照耀且因此更靠近太阳。由同样的论证,当彗星的头隐藏在太阳之下,且有时发出的尾既巨大又明亮,像燃烧的火柱,它们应位于金星的轨道之下。因为,如果假设所有的那些光聚集在一颗星上,它有时不仅会超过金星,而且会超出一些金星的联合。
最后,从彗星的头的光可推断出同样的事情,光在彗星自地球朝向太阳退离时增大,在自太阳朝向地球退离时减小。于是1665年的后一颗彗星(按照赫维留的观测),从开始看见它,它的视运动总在减小,且因此已过了它的近地点,但彗星的头的光亮照样逐日增加,直到彗星被太阳的光线遮盖,终止可见。1683年的彗星(按照同一个赫维留的观测)在7月底,当它初次被看到,它运动得极缓慢,每天在它自己的轨道上约前进40分或者45′。从那时起其运动逐日持续增大,直到9月4日,它达到约五度。所以,在所有这些时间,彗星正靠近地球。这也可以从由测微计测得的彗星的头的直径推断出:因为赫维留在8月6日发现包括彗发的头部仅为6′.5″,在9月2日为9′.7″。所以彗星的头在运动开始时看起来大大小于在运动结束时;但在开始时彗星的头邻近太阳,远比在运动快要结束时明亮,正如同一个赫维留所报告的。所以,在所有这段时间,由于它自太阳退离,其光亮减小,虽然它靠近地球。1618年的彗星(62)约在12月的月中,且1680年的彗星约在同一个月的月底,运动非常迅速,且因此它们那时在它们的近地点。然而它们的头最明亮时发生在约两星期之前,那时它们刚从太阳的光线中离开;且彗尾最明亮的时间略靠前,那时它们更邻近太阳。前一颗彗星的头,按照齐扎特的观测,在12月1日,看起来大于一等星,且在12月16日(那时它在近地点),它在大小上略为减小,而在明亮或者其光的明朗上大为减小。在1月7日,开普勒由于不确知彗星的头而结束了他的观测。在12月12日,后一颗彗星的头可见,并在离太阳九度的一个距离被弗拉姆斯蒂德观测到,仅及一颗三等星。12月15日和17日,彗星的头部如同一颗三等星出现,因为它被邻近日出的云的光亮所减小。在12月26日,它以最大的速度运动,且几乎在它的近地点,弱于飞马座之口(63),这是一颗三等星。在1月3日,它如同一颗四等星出现,1月9日如同一颗五等星,1月13日,由于新月的光亮而不出现。1月25日勉强等于一颗七等星。如果从近地点向两个方向取相等的时间,彗星的头,它在那些时间位于遥远的区域,由于离地球的距离相等,应以相等的光发亮,但在朝向太阳的区域最明亮,并在近地点的另一侧消失。所以,从光在一种情形和另一种情形的大的差异,得出在前一种情形太阳和彗星显著接近。因为彗星的光趋于规则,且当彗星的头运动最迅速时光最大,因此它在近地点;但邻近太阳的范围光变大除外。
系理1 所以诸彗星由于它们反射太阳的光而发光。
系理2 从以上所说也可以理解为何彗星频繁地出现在太阳的区域。如果它们在远高于土星的区域被识别,它们应更频繁地出现在对着太阳的那部分天空。因为它们在那些部分离地球更近,且位于中间的太阳遮盖其他天体。然而我博览彗星的记载,发现在向着太阳的半球被识别的比在对着太阳的半球被识别的多四到五倍,除此之外,无疑相当多的彗星被太阳的光遮盖。的确,当它们下降到我们的区域,既不射出尾巴,又没有被太阳照得如此之亮,以至在它们离我们比木星更近之前能被肉眼发现。但是以如此小的间隔围绕太阳所画的空间的绝大部分在面对太阳的地球的一侧;彗星在那个较大的部分,由于离太阳近得多,通常被照耀得很亮。
系理3 因此,天空缺乏阻力也是显然的。因为彗星顺着倾斜的且有时与行星的路线相反的路径,在各个方向极自由地运动,且它们的运动保持极长的时间,即使与行星的路线相反。若我没有弄错,彗星是一类行星且以持续的运动在返回到自身的轨道上运动。因为一些著作家主张彗星为流星,他们的论证由彗星的头的持续变化引出,似乎没有根据。彗星的头由巨大的大气层包围,且大气层向下应当较致密。所以,那些变化是在云上,而不是彗星的本体上被看到。于是,如果从行星上观看地球,它无疑从自身云的光发亮,且其固态的本体几乎隐藏在云下。因此木星的云带(cingula)由那颗行星的云形成,因为云的位置彼此变化,所以通过那些云很难看到木星的固态的本体。且彗星的本体必定更是隐藏在它们的既深且浓的大气之下。
命题LX 定理XX
诸彗星在圆锥截线上运动,圆锥截线的焦点是太阳的中心,且向太阳所引的半径画出的面积与时间成比例。
通过第一卷中的命题XIII系理1与第三卷中的命题VIII,XII和XIII比较,这是显然的。
系理1 因此,如果彗星在返回到自身的轨道上运行,这些轨道为椭圆,且循环时间比行星的循环时间按照主轴的二分之三次比。彗星,因为绝大部分处于行星之外,且因此以更长的轴画出轨道,运行得较慢。因此,如果彗星的轨道的轴是土星的轨道的轴的四倍,彗星的运行时间比土星的运行时间,亦即,比30年,如同4√4(或者8)比1,且因此为240年。
系理2 但这些轨道与抛物线如此接近,以致用抛物线代替它们不会产生可以感觉到的误差。
系理3 且所以(由第一卷命题XVI系理7),每个彗星的速度比任意围绕太阳在圆形轨道上运行的行星的速度,总是非常接近地按照二倍的行星离太阳的中心的距离比彗星离太阳的中心的距离的二分之一次比。我们假设大轨道的半径,或者地球在其上运行的椭圆的最大的半直径为100000000份;且地球自身的平均周日运动画出1720212份,则小时运动为
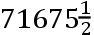 份。且所以彗星在地球离太阳的相同的平均距离上,以一个速度,它比地球的速度如同√2比1,由其周日运动画出2432747份,且由其小时运动画出
份。且所以彗星在地球离太阳的相同的平均距离上,以一个速度,它比地球的速度如同√2比1,由其周日运动画出2432747份,且由其小时运动画出
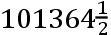 份。但在较大或者较小的距离上,周日运动以及小时运动比这个周日运动和小时运动,按照距离的二分之一次反比,且因此被给定。
份。但在较大或者较小的距离上,周日运动以及小时运动比这个周日运动和小时运动,按照距离的二分之一次反比,且因此被给定。
系理4 因此,如果抛物线的通径是四倍的地球的大轨道的半径,且如果那个半径的平方被取作100000000份:则彗星由向太阳所引的半径每天画出的面积为
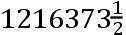 份,且每小时那个面积为
份,且每小时那个面积为
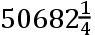 份。但如果通径以任何的比增大或者减小,则彗星的周日面积和小时面积按照同一个比的二分之一次方增大或者减小。
份。但如果通径以任何的比增大或者减小,则彗星的周日面积和小时面积按照同一个比的二分之一次方增大或者减小。
引 理 V
求一条抛物线类的曲线,它穿过任意数目的给定点。
令那些点为A,B,C,D,E,F,等等,且自它们向任意位置给定的直线HN上落下同样多的垂线AH,BI,CK,DL,EM,FN。
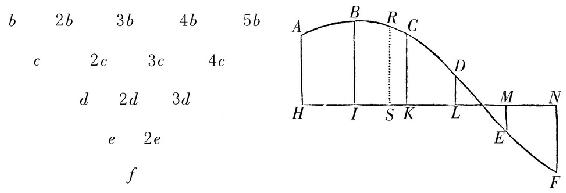
情形1 如果点H,I,K,L,M,N之间的间隔HI,IK,KL,等等相等,列出垂线AH,BI,CK,等等的第一差b,2b,3b,4b,5b,等等,第二差c,2c,3c,4c,等等,第三差d,2d,3d,等等,亦即,在此条件下AH-BI=b,BI-CK=2b,CK-DL=3b,DL+EM=4b,-EM+FN=5b,等等,然后b-2b=c,等等,并如此继续到最终的差,在这里它是f。然后,竖立任意的垂线RS,它是所求曲线的纵标线,为了发现它的长度,假设间隔HI,IK,KL,LM,等等为单位,且令AH=a,-HS=p,
 p乘以-IS=q,
p乘以-IS=q,
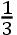 q乘以+SK=r,
q乘以+SK=r,
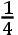 r乘以+SL=s,
r乘以+SL=s,
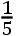 s乘以+SM=t;继续进行,如此一直到倒数第二条垂线ME,且在项HS,IS,等等前缀以负号,它们位于点S向着A的一侧,又在项SK,SL等等前缀以正号,它们位于点S的另一侧。且如果符号[规则]被准确地遵守,则RS=a+bp+cq+dr+es+ft,等等。
s乘以+SM=t;继续进行,如此一直到倒数第二条垂线ME,且在项HS,IS,等等前缀以负号,它们位于点S向着A的一侧,又在项SK,SL等等前缀以正号,它们位于点S的另一侧。且如果符号[规则]被准确地遵守,则RS=a+bp+cq+dr+es+ft,等等。
情形2 如果点H,I,K,L等等之间的间隙不相等,列出垂线AH,BI,CK,等等的第一差除以垂线的间隔:b,2b,3b,4b,5b;第二差除以每两个间隔:c,2c,3c,4c,等等;第三差除以每三个间隔:d,2d,3d,等等,第四差除以每四个间隔:e,2e,等等;且如此继续;亦即,在此条件下,b=(AH-BI)/(HI),2b=(BI-CK)/(IK),3b=(CK-DL)/(KL),等等;其次 c=(b-2b)/(HK),2c=(2b-3b)/(IL),3c=(3b-4b)/(KM),等等;再次,d=(c-2c)/(HL),2d=(2c-3c)/(IM),等等。当已发现这些差,令AH=a,-HS=p,p 乘以-IS=q,q乘以+SK=r,r乘以+SL=s,s乘以+SM=t;继续进行,如此一直到倒数第二条垂线ME,则纵标线RS=a+bp+cq+dr+es+ft,等等。
系理 因此所有曲线的面积可以很近似地求得。因为如果任意要求积的曲线的一些点被发现,且假设经过它们引一抛物线,这条抛物线的面积与那条要求积的曲线的面积非常接近相等。但抛物线总能用习知的方法几何地求积。
引理 VI
从一颗彗星的若干个已观测到的位置,求在任意给定的中间时间它的位置。
指定HI,IK,KL,LM为观测之间的时间(在前图中),HA,IB,KC,LD,ME为五个观测到的彗星的黄经,HS为第一次观测和要求的黄经之间的时间。且如果想象着过点A,B,C,D,E引一条规则的曲线ABCDE;由上面的引理发现其纵标线RS,则RS为要求的黄经。
由同样的方法从五个观测到的彗星的黄纬可发现在一给定时间的黄纬。
如果观测到的黄经之间的差较小,比如说4或者5度;三次或者四次观测就足以发现新的黄经和黄纬。但如果差较大,比如说10或者20度,必须用五次观测。
引理 VII
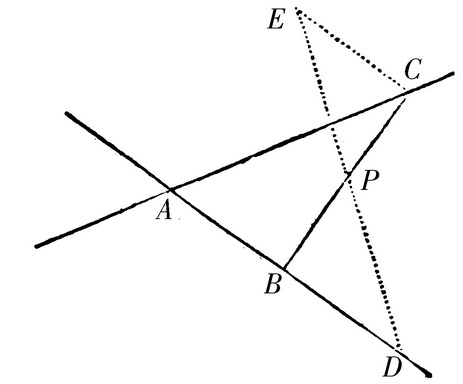
通过给定点P引一直线BC,它的部分PB,PC被位置已给定的两条直线AB和AC割下,它们彼此有给定的比。
从那个点P向两直线之一AB引任意一条直线PD,并向另一直线AC延长同一直线一直到E,使得PE比PD按照那个给定的比。设EC平行于AD;且如果作CPB,则PC比PB如同PE比PD。此即所作。
引理 VIII
设ABC是焦点为S的一条抛物线。弦AC在I被平分并割下弓形ABCI,它的直径为Iμ且顶点为μ。在Iμ的延长上取μO等于Iμ的一半。连结OS,并延长它至ξ,使得Sξ等于2SO。且如果一颗彗星B在弧CBA上运动,又作ξB截AC于E:我说,点E从弦AC上割下的一段AE非常接近地与时间成比例。
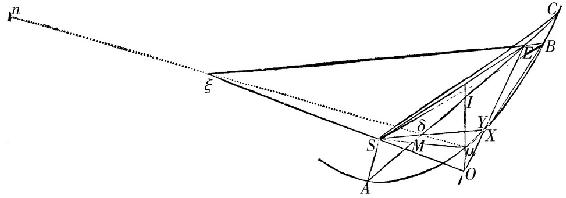
因连结EO截抛物线的弧ABC于Y,且作μX,它切同一弧于顶点μ,并交EO于X;则曲线[形]AEXμA的面积比曲线[形]ACYμA的面积如同AE比AC。且因此,由于三角形ASE比三角形ASC按照相同的比,整个ASEXμA的面积比整个ASCYμA的面积如同AE比AC。但是,由于ξO比SO如同3比1,且EO比XO按照相同的比,SX平行于EB;且所以,如果连结BX,则三角形SEB等于三角形XEB。于是,如果三角形EXB被加到面积ASEXμA上,并从中除去三角形SEB,留下的面积ASBXμA等于ASEXμA,且因此比面积ASCYμA如同AE比AC。但是,面积ASBYμA很接近地等于面积ASBXμA;且这个面积ASBYμA比ASCYμA,如同画出弧AB的时间比画出整个弧AC的时间。且因此AE比AC很接近地按照相同的比。此即所证。
系理 当点B落在抛物线的顶点μ上,AE比AC精确地按照时间之比。
解释
如果连结μξ截AC于δ,且在它之上取ξn,它[ξn]比μB如同27MI比16Mμ;作Bn,则Bn按照较以前更精确的时间之比截弦AC。但是,如果点B离抛物线的主顶点比离点μ远,点n位于点之外;如果点B离同一个顶点较近,则相反。
引理 IX
直线Iμ和μM以及长度(AIC)/(4Sμ)彼此相等。
因4Sμ是属于顶点μ的抛物线的通径。
引理 X
如果延长Sμ至N及P,使得μN等于μI的三分之一,且SP比SN如同SN比Sμ。一颗彗星,在画出弧AμC的一段时间,如果它总以它在等于高度SP时所具有的速度前进,它将画出等于弦AC的一个长度。
因为如果彗星以它在μ所具有的速度在相同的时间在一条直线上均匀地前进,它切抛物线于μ;面积,它由向点S所引的半径画出,等于抛物线的面积ASCμ。且因此在切线上画出的长度和长度Sμ之下的容量比长度AC和SM之下的容量,如同面积ASCμ比三角形ASC,亦即,如同SN比SM。是以AC比在切线上画出的长度,如同Sμ比SN。但是,由于彗星在高度SP的速度(由第一卷命题XVI系理6)比它在高度Sμ的速度,按照SP比Sμ的二分之一次反比,亦即,按照Sμ比SN之比;在相同的时间以这个速度画出的长度,比在切线上画出的长度,如同Sμ比SN。所以,因为AC和以这个新的速度画出的长度,比在切线上画出的长度,按照相同的比,它们彼此相等。此即所证。
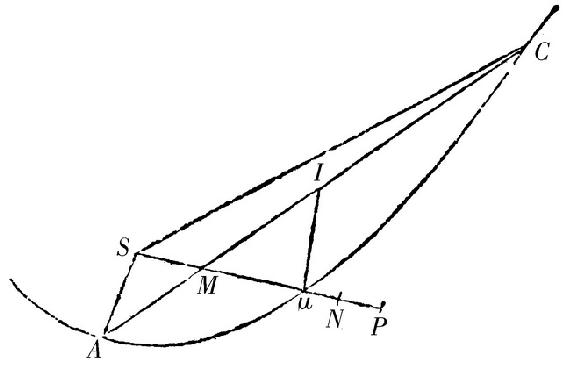
系理 所以,彗星以它在高度Sμ+
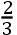 Iμ所具有的速度,在相同的时间,非常接近地画出弦AC。
Iμ所具有的速度,在相同的时间,非常接近地画出弦AC。
引理 XI
如果一颗彗星被夺去所有的运动,从高度SN或者Sμ+(2/3)Iμ坠落,使得它向太阳下落,且彗星一直被一均匀地持续的力推向太阳,在一开始时它即受此力推动;当彗星在自己的轨道上画出弧AC的时间的一半,它在下落中画出等于长度Iμ的一个空间。
因为彗星,在一段时间画出抛物线弧AC,在相同的时间它以在高度SP所具有的速度(由上一引理)画出弦AC,且因此(由第一卷命题XVI系理7)在相同的时间,它在一个圆上,其半直径为SP,以它自身的重力旋转,画出一段弧,其长度比抛物线的弧的弦AC,按照一比二的二分之一次比。且所以它以它在高度SP向着太阳的重量,从那个高度向太阳下落,在那段时间的一半画出的一个空间(由第一卷命题IV系理9)等于那条弦的一半的平方除以四倍的高度SP,亦即,空间(AIq)/(4SP)。由是,因为在高度SN上彗星向着太阳的重量比在高度SP上它向着太阳的重量,如同SP比Sμ;彗星以它在高度SN所具有的重量,在相同的时间向太阳下落,画出空间(AIq)/(4Sμ),亦即,长度等于Iμ或者Mμ的一个空间。此即所证。
命题XLI 问题XXI
由给定的三次观测,确定在抛物线上运动的彗星的轨道。
我曾多方尝试这个非常困难的问题,在第一卷中我撰写了一些问题,它们从属于其解答。其后我想到了如下稍为简单的解法。
选择三次观测,彼此的时间间隔近似地等远。但在那个时间间隔,当时彗星缓慢运动,比另一个略大,即是使得时间的差比时间的和,如同时间的和比差不多六百天;或者使得点E(在引理VIII的图中)落在很靠近点M 的地方,且从那里向I偏离而不是向A偏离。如果不具备如此的观测,必须用引理六发现彗星新的位置。
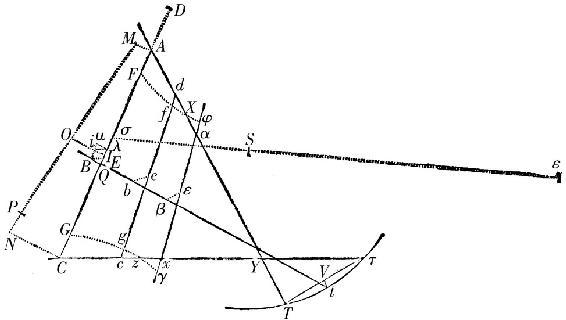
指定S为太阳,T,t,τ为在大轨道上地球的三个位置,TA,tB,τC为三个观测到的彗星的黄经,V为第一次和第二次观测之间的时间,W为第二次和第三次观测之间的时间,X为一段长度,它能由彗星在整个那段时间从它在地球离太阳的平均距离处的速度画出,(由第三卷命题XL系理3)发现这段长度,且tV是弦Tτ的垂线。在中间一次观测到的黄经tB上,任意取一点B作为在黄道的平面上彗星的位置,并由此向太阳S引直线BE,它比矢tV,如同SB和Stquad之下的容量比一个直角三角形的斜边的立方,它的[直角]边为SB和在第二次观测时对半径tB的彗星的黄纬的切线。且过点E引(由本卷中的引理VII)直线AEC,它的部分AE,EC,由直线TA和τC界定,彼此如同时间V和W:则A和C与在第一次和第三次观测时在黄道的平面上的彗星的位置很接近,只要B是在第二次观测时正确地假设的它的位置。
在平分于I的AC上竖立垂线Ii。过点B引想象的直线Bi 平行于AC。连结想象的直线Si,它截AC于λ,并补足平行四边形iIλμ。取Iσ等于3Iλ,并过太阳S引想象的σξ等于3Sσ+3iλ。然后,删去字母A,E,C,I,自点B向点ξ引一条新的想象的直线BE,使得它比原来的BE按照距离BS比量Sμ+
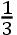 iλ的二次比。且过点E按照与前面相同的定律再引直线AEC,亦即,使得其部分AE和EC彼此如同观测之间的时间V和W。则A和C是彗星的更精确的位置。
iλ的二次比。且过点E按照与前面相同的定律再引直线AEC,亦即,使得其部分AE和EC彼此如同观测之间的时间V和W。则A和C是彗星的更精确的位置。
在平分于I的AC上竖立垂线AM,CN,IO,其中AM和CN是在第一次和第三次观测时对半径TA和τC的黄纬的切线。连结MN截IO于O。作矩形iIλμ如前。在IA的延长线上取ID 等于Sμ+
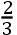 iλ,然后在MN上向着N截取MP,MP比上面发现的长度X,按照地球离太阳的平均距离(或者大轨道的半径)比距离OD的二分之一次比。如果点P落在点N上,则A,B,C为彗星的三个位置,通过它们的轨道被画在黄道的平面上。但如果点P不落在点N上,在直线AC上取CG等于NP,如此使得点G和P位于直线NC的同一侧。
iλ,然后在MN上向着N截取MP,MP比上面发现的长度X,按照地球离太阳的平均距离(或者大轨道的半径)比距离OD的二分之一次比。如果点P落在点N上,则A,B,C为彗星的三个位置,通过它们的轨道被画在黄道的平面上。但如果点P不落在点N上,在直线AC上取CG等于NP,如此使得点G和P位于直线NC的同一侧。
由同样的方法,从假设的点B发现点E,A,C,G,从其他任意假设的b和β发现新的点e,a,c,g和ε,α,κ,γ。然后过G,g,γ画的圆的周线Ggγ截直线τC于Z:则Z为在黄道的平面上彗星的位置。且如果在AC,ac,ακ上取AF,af,αφ分别等于CG,cg,κγ,且过点F,f,φ画的圆的周线Ffφ截直线AT于X;则X为在黄道的平面上彗星的另一个位置。在点X和Z,竖立对半径TX和τZ的彗星的黄纬的切线,则彗星在其轨道上的两个位置被发现,最后(由第一卷命题XIX)以焦点S,过那两个位置画出一抛物线,则这条抛物线是彗星的轨道。此即所求。
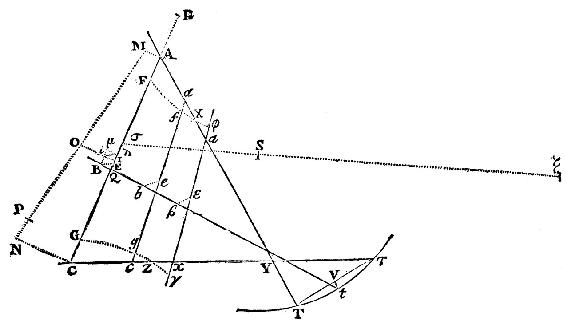
这个做法的证明由诸引理推出:因为由引理VII,直线AC在E按照时间之比被截,正如引理VIII所要求的;且因为BE,由引理XI,是直线BS的或者Bξ的在黄道的平面上位于弧ABC和弦AEC中间的部分;又因为MP(由引理X的系理)是弧的弦的长度,这个弧应由彗星在第一次和第三次观测之间在自己的轨道上画出,且因此等于MN,只要B是在黄道的平面上的彗星的真实位置。
但是,如果不任意地选择点B,b,β,而以接近真的位置选择它们,这是方便的。如果角AQt被近似地知道,轨道在黄道的平面上画出的射影以这个角截直线tB;在那个角引想象的直线AC,它比43Tτ按照SQ比St的二分之一次比。且通过引直线SEB,它的部分EB等于长度Vt,点B被确定,B首先被用到。然后删去AC并按前面的作法重新引一条直线AC,且在发现长度MP之后,在tB上取点b,按照定律,如果TA,τC相互截于Y,则距离Yb比距离YB,按照来自MP比MN的比和SB比Sb的二分之一次比的复合比。且只要心甘情愿重复第三次,按同样的方法发现第三个点β。但这一方法对于大多数情况,两次操作就够了。因为,如果遇到的距离Bb非常小,发现点F、f和G、g之后,引直线Ff和Gg截TA和τC于需求的点X和Z。
例子
问题设为1680年的彗星。彗星的运动经弗拉姆斯蒂德的观测并由他从观测加以计算,再由哈雷根据同样的观测做了修正,显示在下表中。
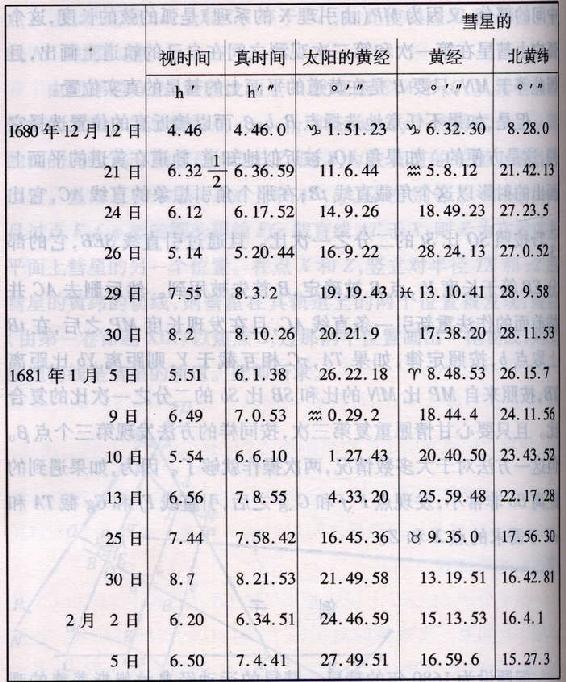
在这些观测上增加我们的一些观测。
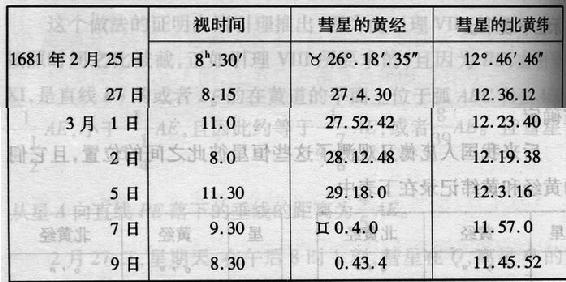
这些观测是用一架带测微计的七呎长的望远镜做的,测微计的线位于望远镜的焦点;用这些仪器我们确定了恒星彼此之间的位置和彗星相对于恒星的位置。指定A为在英仙座左踵上的一颗四等星(在巴耶的星表(64)中为ο),B为紧跟着在脚上的一颗三等星(在巴耶的星表中为ζ),且C为同一踵上的一颗六等星(在巴耶的星表中为n),又D,E,F,G,H,I,K,L,M,N,O,Z,α,β,γ,δ为在同一只脚上的其他较小的星。再设p,P,Q,R,S,T,V,X是以上描述的观测中彗星的位置,且距离AB被认作
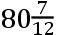 份,AC为
份,AC为
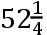 份,BC
份,BC
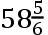 ,AD
,AD
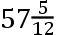 ,BD
,BD
 ,CD
,CD
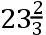 ,AE
,AE
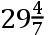 ,CE
,CE
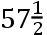 ,DE
,DE
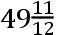 ,AI
,AI
 ,BI
,BI
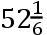 ,CI
,CI
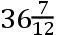 ,DI
,DI
 ,AK
,AK
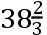 ,BK43,CK
,BK43,CK
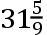 ,FK29,FB23,FC
,FK29,FB23,FC
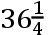 ,AH
,AH
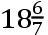 ,DH
,DH
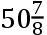 ,BN
,BN
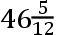 ,CN
,CN
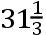 ,BL
,BL
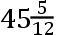 ,NL
,NL
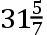 。HO比HI如同7比6且当它延长时从星D和星E之间穿过,于是星D离这条直线的距离为
。HO比HI如同7比6且当它延长时从星D和星E之间穿过,于是星D离这条直线的距离为
 CD。LM比LN如同2比9,且它延长穿过星H。这些恒星彼此之间的位置被确定。
CD。LM比LN如同2比9,且它延长穿过星H。这些恒星彼此之间的位置被确定。
后来我国人庞德又观测了这些恒星彼此之间的位置,且它们的黄经和黄纬记录在下表中。
我观测到彗星相对于恒星的位置如下。
2月25日,星期五,旧历,在午后8时半,彗星在p,它离星E的距离小于
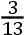 AE,大于
AE,大于
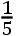 AE,且因此约等于
AE,且因此约等于
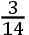 AE;又角ApE稍微有些钝,但几乎是直角。因为自A向pE上落下垂线,彗星离那条垂线的距离为
AE;又角ApE稍微有些钝,但几乎是直角。因为自A向pE上落下垂线,彗星离那条垂线的距离为
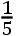 pE。
pE。
在同一个晚上的9时半,彗星在P,离星E的距离(65)大于
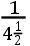 AE,小于
AE,小于
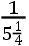 AE,且因此约等于
AE,且因此约等于
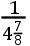 AE,或者
AE,或者
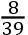 AE。且彗星离从星A向直线PE落下的垂线的距离为
AE。且彗星离从星A向直线PE落下的垂线的距离为
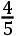 AE。
AE。
2月27日,星期天,在午后8时1刻,彗星在Q,离星O的距离等于星O和H之间的距离,且直线QO延长从星K和B之间穿过。由于中间的云,我未能更精确地确定这条直线的位置。
3月1日,星期二,在午后11时,彗星在R,恰好在星K和C之间,且直线CRK的部分CR稍大于
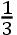 CK,且稍小于
CK,且稍小于
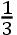 CK+
CK+
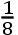 CR,且因此等于
CR,且因此等于
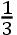 CK+
CK+
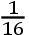 CR或者
CR或者
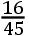 CK。
CK。
3月2日,星期三,在午后8时,彗星在S,离星C的距离约为
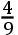 FC。星F离直线CS的延长线的距离为
FC。星F离直线CS的延长线的距离为
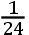 FC;且星B离同一直线的距离,是星F的距离的五倍。同样地,直线NS被延长,从星H和I之间穿过,靠近星H比靠近星I约五倍或者六倍。
FC;且星B离同一直线的距离,是星F的距离的五倍。同样地,直线NS被延长,从星H和I之间穿过,靠近星H比靠近星I约五倍或者六倍。
3月5日,星期六,在午后11时半,彗星在T,直线MT等于
 ML,且直线LT的延长线从B和F之间穿过,靠近F比靠近B约四或者五倍,从BF上割下它朝向F的四分之一或者五分之一。又MT延长时,从空间BF向星B的外边穿过,且靠近星B比靠近星F约四倍。星M很小,用望远镜能勉强看到,而L为大约八等的一颗较大的星。
ML,且直线LT的延长线从B和F之间穿过,靠近F比靠近B约四或者五倍,从BF上割下它朝向F的四分之一或者五分之一。又MT延长时,从空间BF向星B的外边穿过,且靠近星B比靠近星F约四倍。星M很小,用望远镜能勉强看到,而L为大约八等的一颗较大的星。
3月7日,星期一,在午后9时半,彗星在V,直线Vα的延长线从B和F之间穿过,从BF上割下向着F的
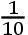 BF,且它比直线Vβ如同5比4。又彗星离直线αβ的距离为
BF,且它比直线Vβ如同5比4。又彗星离直线αβ的距离为
 Vβ。
Vβ。
3月9日,星期三,在午后8时半,彗星在X,直线γX等于
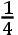 γδ,且自星δ向直线γX落下的垂线为
γδ,且自星δ向直线γX落下的垂线为
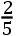 γδ。
γδ。
同一天晚上12时,彗星在Y,直线γY等于
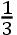 γδ,但略小,设为
γδ,但略小,设为
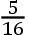 γδ。且自星δ向直线γY落下的垂线约等于
γδ。且自星δ向直线γY落下的垂线约等于
 γδ或者
γδ或者
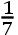 γδ。但由于彗星靠近地平线而难于分辨,其位置的确定自然不能与以上的同样确切。
γδ。但由于彗星靠近地平线而难于分辨,其位置的确定自然不能与以上的同样确切。
通过作图和计算,从这类观测中我导出了彗星的黄经和黄纬,且我国人庞德从修正的恒星的位置修正了彗星的位置,而这些修正了的位置已在上面给出。我使用的测微计制作得不够精致,但黄经和黄纬的误差(就我们观测的范围而言)几乎不超过一分。此外,彗星(按照我们的观测)在其运动结束时明显地由它在2月底占据的平行线上往北倾斜。
现在,为了确定彗星的轨道,我从以上描述的观测中选择三个,它们是弗拉姆斯蒂德在12月21日,1月5日和1月25日做的。从这些观测我发现St为9842.1份,且Vt为455份,若假设大轨道的半直径为10000份。然后,对第一次运算,我假定tB为5657份,我发现SB为9747,BE在第一轮中为412,Sμ 9503,iλ413;BE在第二轮中为421,OD 10186,X 8528.4,MP 8450,MN 8475,NP 25。因此由第二次运算,我推得距离tb为5640。且由这些计算我最终求得距离TX为4775以及τZ为11322。在从这些距离确定轨道时,我发现其降交点在
 在且升交点在
在且升交点在
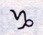 1gr..53′;它的平面对于黄道的平面的倾角为61gr..
1gr..53′;它的平面对于黄道的平面的倾角为61gr..
 ′;其顶点(或者彗星的近日点)离交点8gr..38′远,且以南黄纬7gr..34′在
′;其顶点(或者彗星的近日点)离交点8gr..38′远,且以南黄纬7gr..34′在
 27gr..43′;又其通径为236.8,而且向太阳所引的半径每天画出93585,假设大轨道的半径的平方为100000000;且我发现彗星在这个轨道上按[黄道十二]宫的顺序前进,并在12月8d.0h.4′(66)在轨道的顶点或者近日点。所有这些我是用一条被等分的尺子和角的弦通过绘图定出,角的弦取自自然正弦的表;我作了一张颇大的图表,在其上大轨道的半直径(10000份的)等于一英呎的
27gr..43′;又其通径为236.8,而且向太阳所引的半径每天画出93585,假设大轨道的半径的平方为100000000;且我发现彗星在这个轨道上按[黄道十二]宫的顺序前进,并在12月8d.0h.4′(66)在轨道的顶点或者近日点。所有这些我是用一条被等分的尺子和角的弦通过绘图定出,角的弦取自自然正弦的表;我作了一张颇大的图表,在其上大轨道的半直径(10000份的)等于一英呎的
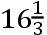 吋。
吋。
最后,为了确定彗星是否真的在这样发现的轨道上运动,我部分地由算术运算且部分地由画图,推算了彗星在一些观测时间在这条轨道上的位置,正如在下表所见。
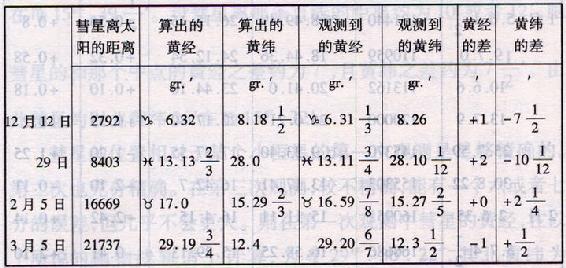
后来,我们的同国人哈雷用算术计算比用画图更精确地确定了[这颗彗星的]轨道;且保持交点在
 和
和
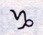 1gr..53′的位置,轨道的平面对黄道的平面的倾角61gr..
1gr..53′的位置,轨道的平面对黄道的平面的倾角61gr..
 ′,以及彗星在近日点的时间12月8d.0h.4′;他发现近日点离升交点的距离在彗星的轨道上测量为9gr..20′,且抛物线的通径为2430份,太阳离地球的平均距离取为100000份。且从这些数据由更精确的算术计算,他计算了在观测时间上彗星的位置,如下表。
′,以及彗星在近日点的时间12月8d.0h.4′;他发现近日点离升交点的距离在彗星的轨道上测量为9gr..20′,且抛物线的通径为2430份,太阳离地球的平均距离取为100000份。且从这些数据由更精确的算术计算,他计算了在观测时间上彗星的位置,如下表。
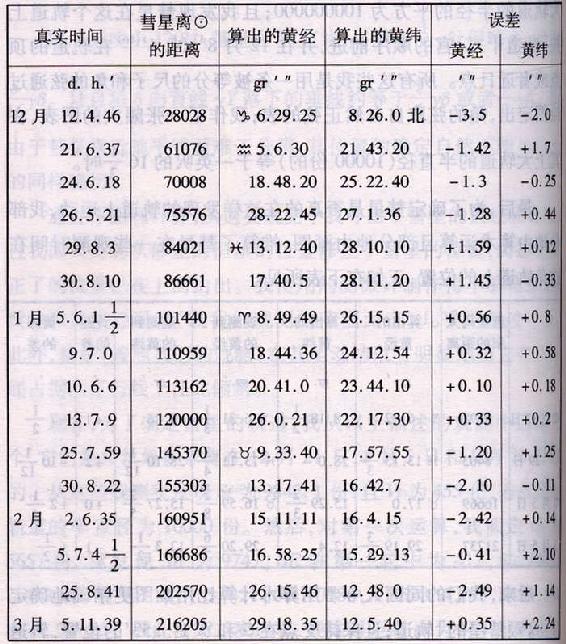
这颗彗星也在更早的11月份出现过,且在萨克森的科堡,由戈特夫里德·柯奇先生在这个月的第四、第六和第十一日,旧历,作了观测,且由其相对于最近的恒星的位置,有时用二呎长的望远镜,有时用十呎长的望远镜,观测相当精确,由科堡的和伦敦的十一度的经度差和由我们的同国人庞德观测的恒星的位置,我们的同国人哈雷确定了彗星的位置如下。
在伦敦的视时间11月3d.17h.2′,彗星以北黄纬1gr..17′.45″在
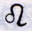 29gr..51′。
29gr..51′。
11月5d.15h.48′,彗星以北黄纬1gr..6′在
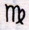 3gr..23′。
3gr..23′。
11月10d.16h.31′,彗星离狮子座中在巴耶的星表中被记为σ和τ的星等距;它尚未触及连结它们的直线,但相离它很近。在弗拉姆斯蒂德的星表中σ以北黄纬1gr..41′在
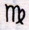 14gr..15′,τ以南黄纬0gr..34′在
14gr..15′,τ以南黄纬0gr..34′在
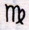 17gr.
17gr.
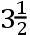 ′。且这些星的中点以南黄纬0gr..
′。且这些星的中点以南黄纬0gr..
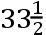 ′在
′在
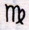 15gr..
15gr..
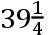 ′。设彗星离那条直线的距离约为10′或者12′,则彗星的和那个中点的黄经之差约为7′,且黄纬之差约为
′。设彗星离那条直线的距离约为10′或者12′,则彗星的和那个中点的黄经之差约为7′,且黄纬之差约为
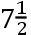 ′。由此彗星约以北黄纬26′在
′。由此彗星约以北黄纬26′在
 15gr..32′。
15gr..32′。
彗星的位置相对于某个小恒星的第一次观测是足够精确的。第二次也充分精确。在第三次观测,较不精确,能有一个六或者七分的误差,但几乎不会更大。则在第一次观测中彗星的黄经,在以上所说的抛物线轨道上计算,为
 29gr..30′.22″,其北黄纬为1gr..25′.7″,再者它离太阳的距离为115546。
29gr..30′.22″,其北黄纬为1gr..25′.7″,再者它离太阳的距离为115546。
此外,哈雷注意到一颗奇异的彗星,它以575年的间隔已出现四次,即在尤利乌斯·凯撒被谋杀后的9月,公历(anno Christi)531年当拉姆帕迪乌斯和奥雷斯特斯为执政官时,公历1106年2月,以及1680年的年底,且这颗彗星带一个长而且显著的尾(除了凯撒之死那年,由于地球的位置不相宜,彗尾看起来较小);他寻求其轴为1382957份的椭圆轨道,地球离太阳的平均距离取为10000份;在这轨道上彗星能以575年的间隔循环。且置升交点在
 2gr..2′;轨道的平面对于黄道的平面的倾角为61gr..6′.48″,彗星的近日点在这个平面上的
2gr..2′;轨道的平面对于黄道的平面的倾角为61gr..6′.48″,彗星的近日点在这个平面上的
 22gr..44′.25″;近日点的平时(tempus æquatum)是12月7d.23h.9′;在黄道的平面上近日点离升交点的距离是9gr..17′.35″;且共轭轴为18481.2;他计算了彗星在这条椭圆轨道上的运动。这个彗星的位置,从观测导出的以及从这条轨道计算所得的,展示在下表中。
22gr..44′.25″;近日点的平时(tempus æquatum)是12月7d.23h.9′;在黄道的平面上近日点离升交点的距离是9gr..17′.35″;且共轭轴为18481.2;他计算了彗星在这条椭圆轨道上的运动。这个彗星的位置,从观测导出的以及从这条轨道计算所得的,展示在下表中。
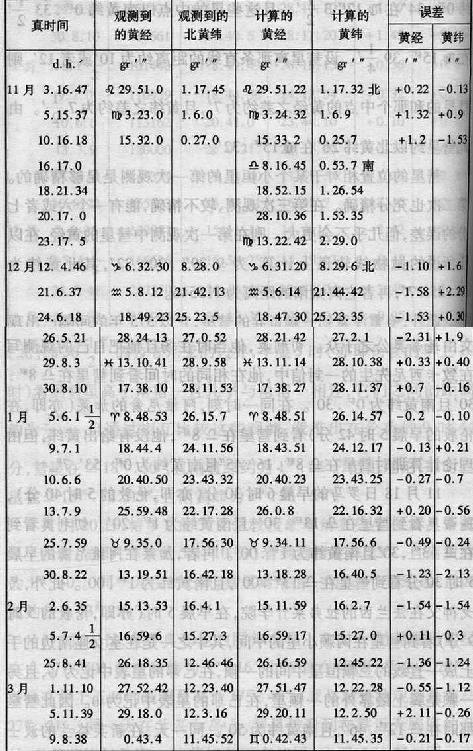
自始至终对这颗彗星的观测与在刚才描述的轨道上彗星的运动的符合,并不比通常行星的运动与行星理论的符合差,且这一符合证明在所有那些时候出现的是一颗且是同一颗彗星,再者,它的轨道已在这里被正确地确定了。
在前面的表中我们已经略去11月16、18、20和23日的观测,由于它们较不精确。因为在那些时刻彗星亦被他人观测。蓬蒂奥和他的同伴在11月17日,旧历,在罗马的早上六时,亦即伦敦的5时10分,用对着恒星的线观察到彗星以南黄纬0gr..40′在
 8gr..30′。他们的观测可在论及这颗彗星的一篇论文中找到,该文由蓬蒂奥公之于众。切利奥,他当时在场且他把自己的观测写在致卡西尼先生的一封信中,他在相同的时间看到彗星在
8gr..30′。他们的观测可在论及这颗彗星的一篇论文中找到,该文由蓬蒂奥公之于众。切利奥,他当时在场且他把自己的观测写在致卡西尼先生的一封信中,他在相同的时间看到彗星在
 8gr..30′且南黄纬为0gr..30′。在同一时刻,阿维尼翁的加莱(亦即,在伦敦的早晨5时42分)看到彗星在
8gr..30′且南黄纬为0gr..30′。在同一时刻,阿维尼翁的加莱(亦即,在伦敦的早晨5时42分)看到彗星在
 8gr.,他没有给出黄纬,但由理论计算那时彗星在
8gr.,他没有给出黄纬,但由理论计算那时彗星在
 8gr..16′.45″且南黄纬为0gr..53′.7″。
8gr..16′.45″且南黄纬为0gr..53′.7″。
11月18日罗马的早晨6时30分(亦即,伦敦的5时40分),蓬蒂奥看到彗星在
 13gr..30′,且南黄纬为1gr..20′。切利奥看到在
13gr..30′,且南黄纬为1gr..20′。切利奥看到在
 13gr..30′且南黄纬为1gr..00′。再者,加莱在阿维尼翁的早晨5时30分看到彗星在
13gr..30′且南黄纬为1gr..00′。再者,加莱在阿维尼翁的早晨5时30分看到彗星在
 13gr..00′,且南黄纬为1gr..00′。此外,昂戈神父在法兰西的拉弗莱什学院,在早晨5时(亦即,伦敦的5时9分)看到彗星在两颗小星的中间,其中之一是在室女座南边的手上成一直线的三颗恒星中间的一颗,在巴耶的星表中记为ψ,且另一颗是翼上最靠外的一颗星,在巴耶的星表中记为θ。因此彗星那时在
13gr..00′,且南黄纬为1gr..00′。此外,昂戈神父在法兰西的拉弗莱什学院,在早晨5时(亦即,伦敦的5时9分)看到彗星在两颗小星的中间,其中之一是在室女座南边的手上成一直线的三颗恒星中间的一颗,在巴耶的星表中记为ψ,且另一颗是翼上最靠外的一颗星,在巴耶的星表中记为θ。因此彗星那时在
 12gr..46′,且南黄纬为50′。同一天,在新英格兰的波士顿,它在[北]纬
12gr..46′,且南黄纬为50′。同一天,在新英格兰的波士顿,它在[北]纬
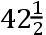 度,早晨5时(亦即伦敦的早上9时44分),彗星被看到临近
度,早晨5时(亦即伦敦的早上9时44分),彗星被看到临近
 14gr.,且南黄纬为1gr..30′,正如杰出的哈雷告知我的。
14gr.,且南黄纬为1gr..30′,正如杰出的哈雷告知我的。
11月19日在剑桥早晨的四时半,彗星(按照一位青年的观测)离角宿一(spica virginis)向西北约2gr.远。但是角宿一在
 19gr..23′.47″,且南黄纬为2gr..1′.59″。同一天,在新英格兰的波士顿的早上5时,彗星离角宿一的间隔约一度远,黄纬的差为40′。在同一天的牙买加岛,彗星离角宿一约一度远。在同一天,阿瑟·斯托勒先生在帕塔克森特河,它邻近马里兰的亨廷克里克,在[北]纬
19gr..23′.47″,且南黄纬为2gr..1′.59″。同一天,在新英格兰的波士顿的早上5时,彗星离角宿一的间隔约一度远,黄纬的差为40′。在同一天的牙买加岛,彗星离角宿一约一度远。在同一天,阿瑟·斯托勒先生在帕塔克森特河,它邻近马里兰的亨廷克里克,在[北]纬
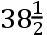 gr.的弗吉尼亚的边界,早晨5时(亦即伦敦的早上10时)看到彗星高于角宿一且几乎与角宿一相连,它们之间的距离约为
gr.的弗吉尼亚的边界,早晨5时(亦即伦敦的早上10时)看到彗星高于角宿一且几乎与角宿一相连,它们之间的距离约为
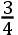 gr.。且通过相互比较这些观测,我推出在伦敦的9时44分,彗星在
gr.。且通过相互比较这些观测,我推出在伦敦的9时44分,彗星在
 18gr..50′,且南黄纬约为1gr..25′。但由理论,那时彗星在
18gr..50′,且南黄纬约为1gr..25′。但由理论,那时彗星在
 18gr..52′.15″,且南黄纬为1gr..26′.54″。
18gr..52′.15″,且南黄纬为1gr..26′.54″。
11月20日,帕多瓦的天文学教授蒙塔纳里先生在威尼斯的早上六时(亦即,伦敦的5时10分)看到彗星在
 23gr.,且南黄纬为1gr..30′。同一天在波士顿,彗星离角宿一向东4gr.黄经远,且因此约在
23gr.,且南黄纬为1gr..30′。同一天在波士顿,彗星离角宿一向东4gr.黄经远,且因此约在
 23gr..24′。
23gr..24′。
11月21日,蓬蒂奥和他的同伴在早上7时1刻观测到彗星在
 27gr..50′,且南黄纬为1gr..16′;切利奥的观测,是在
27gr..50′,且南黄纬为1gr..16′;切利奥的观测,是在
 28gr.。昂戈在早上五时的观测是在
28gr.。昂戈在早上五时的观测是在
 27gr..45′。蒙塔纳里的观测是在
27gr..45′。蒙塔纳里的观测是在
 27gr..51′。同一天在牙买加岛上,彗星被看到在靠近天蝎座的开始,且其黄纬与角宿一的黄纬差不多相同,亦即,2gr..2′。同一天在东印度的巴拉索尔的早上五时(亦即,伦敦的前一天晚上的11时20分),得到彗星离角宿一向东7gr..35′远。在角宿一和[天秤座的]秤盘之间的直线上,且因此在
27gr..51′。同一天在牙买加岛上,彗星被看到在靠近天蝎座的开始,且其黄纬与角宿一的黄纬差不多相同,亦即,2gr..2′。同一天在东印度的巴拉索尔的早上五时(亦即,伦敦的前一天晚上的11时20分),得到彗星离角宿一向东7gr..35′远。在角宿一和[天秤座的]秤盘之间的直线上,且因此在
 26gr..58′,且南黄纬约为1gr..11′;又后来在5时40分(即在伦敦的早上五时)它在
26gr..58′,且南黄纬约为1gr..11′;又后来在5时40分(即在伦敦的早上五时)它在
 28gr..12′,且南黄纬为1gr..16′。由理论计算彗星那时在
28gr..12′,且南黄纬为1gr..16′。由理论计算彗星那时在
 28gr..10′.36″,且南黄纬为1gr..53′.35″。
28gr..10′.36″,且南黄纬为1gr..53′.35″。
11月22日,彗星被蒙塔纳里看到在
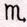 2gr..33′,但在新英格兰的波士顿它大约出现在
2gr..33′,但在新英格兰的波士顿它大约出现在
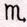 3gr.,黄纬同前,亦即1gr..30′。同一天在巴拉索尔的早上5时,彗星被观测到在
3gr.,黄纬同前,亦即1gr..30′。同一天在巴拉索尔的早上5时,彗星被观测到在
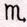 1gr..50′;且因此在伦敦的早上5时,彗星约在
1gr..50′;且因此在伦敦的早上5时,彗星约在
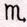 3gr..5′。同一天在伦敦的早上六时半,我们的同国人胡克看到彗星约在
3gr..5′。同一天在伦敦的早上六时半,我们的同国人胡克看到彗星约在
 3gr..30′,且它在穿过角宿一和轩辕十四(cor leonis)的一条直线上,但不尽精确,离开那条直线略向北偏。蒙塔纳里同样注意到彗星通过角宿一引的直线,在这一天和接下来的一天,穿过轩辕十四的南侧,轩辕十四和这条线之间的间隔甚小。穿过轩辕十四和角宿一的直线,以2gr..51′的角截黄道于
3gr..30′,且它在穿过角宿一和轩辕十四(cor leonis)的一条直线上,但不尽精确,离开那条直线略向北偏。蒙塔纳里同样注意到彗星通过角宿一引的直线,在这一天和接下来的一天,穿过轩辕十四的南侧,轩辕十四和这条线之间的间隔甚小。穿过轩辕十四和角宿一的直线,以2gr..51′的角截黄道于
 3gr..46′。且如果彗星曾位于这条直线上且在
3gr..46′。且如果彗星曾位于这条直线上且在
 3gr.,它的黄纬应为2gr..26′。但由于彗星,胡克和蒙塔纳里同意,离开这条直线向北稍有距离,其黄纬略小。20日,由蒙塔纳里的观测,其黄纬几乎等于角宿一的黄纬,即约为1gr..30′,又胡克、蒙塔纳里和昂戈同意,黄纬持续增大,且因此现在明显的大于1gr..30′。在现在建立的界限2gr..26′和1gr..30′之间,平均黄纬的大小约为1gr..58′。彗星的尾,胡克和蒙塔纳里同意,指向角宿一,自这个星稍有倾斜,按胡克为向南,按蒙塔纳里为向北;且因此这个倾斜很难察觉,且彗星的尾几乎与赤道平行,自太阳的对面略向北倾斜。
3gr.,它的黄纬应为2gr..26′。但由于彗星,胡克和蒙塔纳里同意,离开这条直线向北稍有距离,其黄纬略小。20日,由蒙塔纳里的观测,其黄纬几乎等于角宿一的黄纬,即约为1gr..30′,又胡克、蒙塔纳里和昂戈同意,黄纬持续增大,且因此现在明显的大于1gr..30′。在现在建立的界限2gr..26′和1gr..30′之间,平均黄纬的大小约为1gr..58′。彗星的尾,胡克和蒙塔纳里同意,指向角宿一,自这个星稍有倾斜,按胡克为向南,按蒙塔纳里为向北;且因此这个倾斜很难察觉,且彗星的尾几乎与赤道平行,自太阳的对面略向北倾斜。
11月23日,旧历,纽伦堡的早上五时(亦即伦敦的四时半)齐墨尔曼先生看到彗星在
 8gr..8′,且南黄纬为2gr..31′,当然,它的距离由恒星确定。
8gr..8′,且南黄纬为2gr..31′,当然,它的距离由恒星确定。
11月24日,在太阳升起前彗星被蒙塔纳里看到在
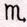 12gr..52′,在穿过轩辕十四和角宿一所引的直线的北侧,且因此它所具有的黄纬略小于2gr..38′。这个黄纬,正如我们所说,按照蒙塔纳里,昂戈和胡克的观测,持续增大;且因此现在略大于1gr..58′;且其平均大小能取作2gr..18′,没有可辨认出的误差。现在蓬蒂奥和加莱要黄纬减小,而切利奥和在新英格兰的一位观测者几乎要黄纬保持相同的大小,即1度或者1度半。蓬蒂奥和切利奥的观测是粗略的,尤其是由方位角和高度取得的,加莱的那些也是如此;由蒙塔纳里、胡克、昂戈以及在新英格兰的那位观测者,再者有时由蓬蒂奥和切利奥以彗星相对于恒星的位置取得的结果较好。同一天在巴拉索尔的早上五时,彗星被观测到在
12gr..52′,在穿过轩辕十四和角宿一所引的直线的北侧,且因此它所具有的黄纬略小于2gr..38′。这个黄纬,正如我们所说,按照蒙塔纳里,昂戈和胡克的观测,持续增大;且因此现在略大于1gr..58′;且其平均大小能取作2gr..18′,没有可辨认出的误差。现在蓬蒂奥和加莱要黄纬减小,而切利奥和在新英格兰的一位观测者几乎要黄纬保持相同的大小,即1度或者1度半。蓬蒂奥和切利奥的观测是粗略的,尤其是由方位角和高度取得的,加莱的那些也是如此;由蒙塔纳里、胡克、昂戈以及在新英格兰的那位观测者,再者有时由蓬蒂奥和切利奥以彗星相对于恒星的位置取得的结果较好。同一天在巴拉索尔的早上五时,彗星被观测到在
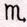 11gr..45′,且因此在伦敦的早上五时它约在
11gr..45′,且因此在伦敦的早上五时它约在
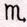 13gr.。由理论计算,彗星在那时在
13gr.。由理论计算,彗星在那时在
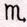 13gr..22′.42″。
13gr..22′.42″。
11月25日,在太阳升起之前,蒙塔纳里观测到彗星约在
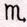
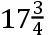 gr.。且在同一时间切利奥观察到彗星在室女座的右股上的一颗亮星和天秤座的南边的秤盘之间的直线上,且这条直线截彗星的道路于
gr.。且在同一时间切利奥观察到彗星在室女座的右股上的一颗亮星和天秤座的南边的秤盘之间的直线上,且这条直线截彗星的道路于
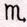 18gr..36′。由理论计算,彗星在那个时间约在
18gr..36′。由理论计算,彗星在那个时间约在
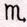
 gr.。
gr.。
所以这些观测与理论符合,依照它们彼此相符的标准,且由这一相符证明那是一颗且是同一颗彗星,它从[1680年]11月4日到[1681年]3月9日的整个时间出现。这颗彗星的轨道截黄道的平面两次,且所以它不是一条直线。它不在天空的相对部分与黄道相截,而在室女宫的结束和摩羯宫的开始,间隔约98度;且因此彗星的路径甚为偏离一个极大的圆。因为在11月,其路径从黄道向南至少倾斜三度,且后来在12月从黄道向北倾斜29度,轨道的两部分,彗星在其上奔向太阳又从太阳返回,彼此倾斜的视角超过三十度,正如蒙塔纳里的观察。这颗彗星在行进中经过九个宫,即从狮子宫的末尾到双子宫的开始;狮子宫除外,因为经过它前进时在能被看到之前;且没有其他理论,按照这一理论彗星能以规则的运动经历如此大的天空部分。它的运动是极为不等的。因为它在11月20日前后,每天约画出五度;此后其运动在11月26日和12月12日之间被迟滞,即在十五天半的时间,它仅画出40度;此后运动被加速,它每天差不多画出五度,直至运动开始被再次迟滞。且一项理论,它与经过天空的极大部分的如此不均匀的运动非常相符,遵守与行星理论相同的定律,又与精确的天文观测准确符合,不会是不正确的。
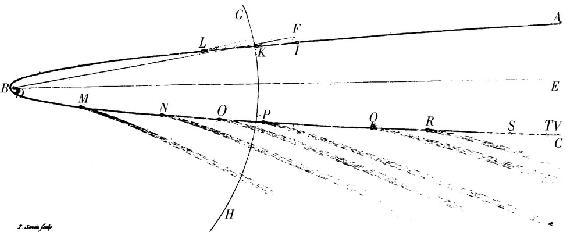
此外,彗星画出的轨道以及在一些位置抛射出的真实的尾,由在轨道的平面上描绘的附图展示是适宜的:这里ABC表示彗星的轨道,D为太阳,DE为轨道的轴,DF为交点线,GH为大轨道的球与轨道的平面的相交部分;I为1680年11月4日彗星的位置;K为11月11日它的位置;L为11月19日它的位置;M为12月12日它的位置;N为12月21日它的位置;O为12月29日它的位置;P为次年1月5日它的位置;Q为1月25日它的位置;R为2月5日它的位置;S为2月25日它的位置;T为3月5日它的位置,且V为3月9日它的位置。在确定彗尾时,我使用了如下的观测。
11月4日和6日,彗尾还没有出现。11月11日,彗尾开始能被看到,通过十呎的望远镜观看不超过半度长。11月17日,彗尾被蓬蒂奥看到超过十五度长。11月18日,彗尾在新英格兰被看到有30gr.长,且正对太阳,并一直延伸到星♂,它[火星]当时在
 9gr..54′。11月19日,在马里兰,彗尾被看到有15或者20度长。12月10日,彗尾(根据弗拉姆斯蒂德的观测)从蛇夫座的巨蛇尾和天鹰座南翼的星δ之间的中间距离穿过,且终止处靠近巴耶的星表中的星A,ω,b。所以彗星的尾终止于
9gr..54′。11月19日,在马里兰,彗尾被看到有15或者20度长。12月10日,彗尾(根据弗拉姆斯蒂德的观测)从蛇夫座的巨蛇尾和天鹰座南翼的星δ之间的中间距离穿过,且终止处靠近巴耶的星表中的星A,ω,b。所以彗星的尾终止于
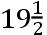 gr.,且北黄纬约为
gr.,且北黄纬约为
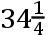 gr.。12月11日,彗尾升高到天箭座的头(巴耶星表中的α,β),终止于
gr.。12月11日,彗尾升高到天箭座的头(巴耶星表中的α,β),终止于
 26gr..43′,且北黄纬为38gr..34′。12月12日,彗尾穿过天箭座的中间,没有太大的伸展,终止于
26gr..43′,且北黄纬为38gr..34′。12月12日,彗尾穿过天箭座的中间,没有太大的伸展,终止于
 4gr.,且北黄纬约为
4gr.,且北黄纬约为
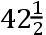 gr.。这些情形被理解为彗尾的较亮的部分的长度。因为当光线较暗,在也许较晴朗的天空,在12月12日罗马的5时40分(根据蓬蒂奥的观测)彗尾高于天鹅座之尾(67)至10度;且其边自这颗星向西北终止于45分。但在那些天向着彗尾在邻近其靠上的一端有3度宽,且因此它的中间离那颗星向南有2gr..15′远,且其上端以北黄纬61gr.终止于
gr.。这些情形被理解为彗尾的较亮的部分的长度。因为当光线较暗,在也许较晴朗的天空,在12月12日罗马的5时40分(根据蓬蒂奥的观测)彗尾高于天鹅座之尾(67)至10度;且其边自这颗星向西北终止于45分。但在那些天向着彗尾在邻近其靠上的一端有3度宽,且因此它的中间离那颗星向南有2gr..15′远,且其上端以北黄纬61gr.终止于
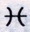 22gr.。且因此彗尾约70gr.长。12月21日,彗尾几乎伸展到仙后座的座尾,离[星]β和王良四(Schedir)等距,且离它们其中一个的距离等于它们彼此之间的距离,且因此终止于
22gr.。且因此彗尾约70gr.长。12月21日,彗尾几乎伸展到仙后座的座尾,离[星]β和王良四(Schedir)等距,且离它们其中一个的距离等于它们彼此之间的距离,且因此终止于
 24gr.,又黄纬为
24gr.,又黄纬为
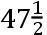 gr.。12月29日,彗尾触到室宿二(Scheat),此星位于它的左边,并精确地填满了仙女座的北边的脚上的两颗星之间的间隔,有54gr.长;且因此终止于
gr.。12月29日,彗尾触到室宿二(Scheat),此星位于它的左边,并精确地填满了仙女座的北边的脚上的两颗星之间的间隔,有54gr.长;且因此终止于
 19gr.,又黄纬为35gr.。1月5日,彗尾触到仙女座胸上的星π的右侧和在她的腰带上的星μ的左侧;且(按照我们的观测)它有40gr.长;但它是弯曲的,且凸的一侧朝南。靠近彗星的头它与经过太阳和彗星的头的圆成一个4度的角;但朝向另一端它以约10或者11度的角向那个圆倾斜且彗尾的弦与圆包含一个8度的角。在1月13日,彗尾明显被看到的光终止于天大将军一(Alamech)和大陵五(Algol)之间,且以微弱的光在向着在英仙座星κ的一侧终止。彗尾的末端离连结太阳和彗星的圆的距离是3gr..50′,且彗尾的弦对那个圆的倾角为
19gr.,又黄纬为35gr.。1月5日,彗尾触到仙女座胸上的星π的右侧和在她的腰带上的星μ的左侧;且(按照我们的观测)它有40gr.长;但它是弯曲的,且凸的一侧朝南。靠近彗星的头它与经过太阳和彗星的头的圆成一个4度的角;但朝向另一端它以约10或者11度的角向那个圆倾斜且彗尾的弦与圆包含一个8度的角。在1月13日,彗尾明显被看到的光终止于天大将军一(Alamech)和大陵五(Algol)之间,且以微弱的光在向着在英仙座星κ的一侧终止。彗尾的末端离连结太阳和彗星的圆的距离是3gr..50′,且彗尾的弦对那个圆的倾角为
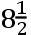 gr.。1月25和26日,彗尾以弱光闪烁至6到7度;且大约一夜之后,当时天空极为晴朗,它的长度延伸到十二度或者更多些,光很弱且几乎不能被看到,但它的轴正对着在御夫座东肩上的亮星,且因此从太阳的对面向北以十度的角倾斜。然后在2月10日,彗尾被我装备[望远镜]的眼睛看到有二度长。因为上面提到的更弱的光通过玻璃不出现。但蓬蒂奥写道,在2月7日他看到长度为12度的彗尾。2月25日以及以后彗星没有尾出现。
gr.。1月25和26日,彗尾以弱光闪烁至6到7度;且大约一夜之后,当时天空极为晴朗,它的长度延伸到十二度或者更多些,光很弱且几乎不能被看到,但它的轴正对着在御夫座东肩上的亮星,且因此从太阳的对面向北以十度的角倾斜。然后在2月10日,彗尾被我装备[望远镜]的眼睛看到有二度长。因为上面提到的更弱的光通过玻璃不出现。但蓬蒂奥写道,在2月7日他看到长度为12度的彗尾。2月25日以及以后彗星没有尾出现。
任何现在思考已描述的轨道且在他的心中回想这颗彗星的其他现象的人,不难认定,彗星的本体是固态的、紧密的、固定的和耐久的,像行星的本体。因为如果彗星不是别的而是蒸汽或者地球的、太阳的以及行星的蒸发水分,这颗彗星在它自己的路径中经过太阳的近处时应会立刻消灭。因为太阳的热如同[它的]光线的密度,这就是,与位置离太阳的距离的平方成反比。且因此,由于在12月8日,当彗星在它的近日点时,它离太阳的中心的距离比地球离太阳的中心的距离大约如同6比1000,在那时太阳在彗星上的热比夏天太阳在我们这里的热如同1000000比36,或者28000比1。但沸腾的水的热约比干燥的地在夏天的太阳下吸收的热大三倍,正如我从经验得知的;且白热的铁的热(如果我猜得正确)约比沸腾的水的热大三或者四倍;且由此,彗星上的干地在彗星处于它的近日点时从太阳的光线所吸收的热,约比白热的铁的热大2000倍。对如此大的热,蒸汽和蒸发水分,以及所有的挥发性的物质立即被耗尽并消灭。
所以彗星在它自己的近日点从太阳吸收极多的热,且那些热能保持极长的时间。因为一吋宽的白热的铁球,在空气中一小时的时间很难失去其所有的热。但较大的球按直径的比保持更长时间的热,因为它的表面(是一个度量,按照表面球通过与周围的空气接触而被冷却)按照那个比相对于它所包含的热的物质的量较小。且因此一个等于这个地球的白热的铁球,亦即,宽约为40000000呎,在相等的天数,或者约50000年,才勉强被冷确。但我怀疑热的持续,由于一些隐匿的原因,按照小于直径的比增加,而且我期望通过实验研究真正的比。
此外,应注意到在12月,当彗星新近被太阳加热,它发射出比在此前的11月大得多且光彩得多的尾,然而它还未到达近日点。且一般地,起源于彗星的所有最大且最灿烂的尾,紧随在它们通过太阳的区域的路径中。所以被灼热的彗星助长其尾的大小。且因此我相信能推断出彗尾不是别的而是极稀薄的蒸汽,它由彗星的头或者核由于自身的热而发射。
然而关于彗星的尾有三种意见:它们或者是太阳的光通过彗星的透明的头部的传播,或者起源于光从彗星的头到地球前进时的折射,或者最后,它们是不断地产生于彗星的头的云或者蒸汽,并向离开太阳的方向跑去。持有第一种意见的人尚未受到光学科学的陶冶,因为进入暗室中的太阳的光不能被分辨出来,除非在空气中飞舞的灰尘和烟的小颗粒反射太阳的光;且因此在浓烟弥漫的空中,太阳的光显得更亮,并且更强地触及视觉;在晴天的空气中这些光较暗淡且不易被感觉到,但在没有物质反射这些光的天空,它们一点也不能被看到。光不是在有光的地方被看到,而是在当它被反射到我们的眼睛的地方被分辨出来。因为视觉不会发生,除非通过射入眼睛的光线。所以在彗尾的区域必定存在某些反射物质,否则整个天空受太阳的光照射均匀地发亮。第二种意见被许多困难所包围。彗尾从来没有被改变颜色,而颜色通常是折射的不可分离的相伴者。恒星的和行星的光到我们这里的明晰的传播证明天空的介质没有反射的能力。据说埃及人有时曾看到有头发的恒星,但这极难遇到,应当归之于云的偶然折射。恒星的光彩和闪烁既由于眼睛的折射又由于颤动的空气的折射,因为当通过望远镜看这些星时它们消失了。由于空气的和上升的蒸汽的颤动,会发生光线交替地从瞳孔的狭窄空间偏斜,但通过[望远镜的]物镜宽的入口则不会发生这样的事情。且因此它是在前一种情形产生的闪烁,但在后一种情形停止;且在后一种情形的停止证明在天空中光规则地传播,没有任何可以感觉到的折射。但是,为了避免以当彗星的光线不够强时通常看不到彗尾,因为次等光线没有足够的力量影响眼睛,且这就是看不到恒星的尾的原因为理由反对时,应考虑到恒星的光用望远镜可以被增大到超过一百倍,但仍看不到尾。行星的光更丰富但没有尾,且当彗星的头的光微弱且很昏暗时,彗星往往有极大的尾。1680年的彗星就是如此,在12月,在彗星的头的光刚及二等星时,它抛射出的彗尾非常明亮,长度可达40,50,60或者70度,甚至更大;此后在1月27日和28日,彗星的头勉强如同一颗七等星出现,但彗尾以微弱但是可以感觉到的光在长度上延伸至6或者7度,且以几乎不能被看到的极暗淡的光,延伸到十二度或者略多,正如以上所说。但在2月9日和10日,当时肉眼看不到彗星的头,通过望远镜我观察到二度长的彗尾。而且,如果彗尾起源于天体物质的折射,且如果它按照天空的形状从太阳的对面偏转,在天空的相同区域,那个偏转总应发生在相同的方向。但是,1680年的彗星,在12月28日伦敦的午后八时半,它在
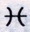 8gr..41′,且北黄纬为28gr..6′,太阳出现在
8gr..41′,且北黄纬为28gr..6′,太阳出现在
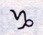 18gr..26′。又1577年的彗星,在12月29日,它在
18gr..26′。又1577年的彗星,在12月29日,它在
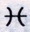 8gr..41′,且北黄纬为28gr..40′,太阳也大约出现在
8gr..41′,且北黄纬为28gr..40′,太阳也大约出现在
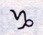 18gr..26′。在两种情形中,地球在相同的位置而彗星出现在天空的相同部分;然而在前一种情形,彗星的尾(根据我的和其他人的观测)从太阳的对面向北有
18gr..26′。在两种情形中,地球在相同的位置而彗星出现在天空的相同部分;然而在前一种情形,彗星的尾(根据我的和其他人的观测)从太阳的对面向北有
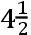 度角的一个倾斜,在后一种情形(根据第谷的观测)向南的倾角为21度。所以,由于被天空的折射所拒绝,余下的是从其他反射光的物质导出彗尾的现象。
度角的一个倾斜,在后一种情形(根据第谷的观测)向南的倾角为21度。所以,由于被天空的折射所拒绝,余下的是从其他反射光的物质导出彗尾的现象。
而且由彗尾遵守的定律证实,彗尾起源于彗星的头且升高到背离太阳的区域。例如在穿过太阳的彗星的轨道的平面上的彗尾,它们总从正对着太阳偏转并指向彗星在那些轨道上前进时留在后面的区域。对一个被安置在那些平面上的观察者,它们出现在正对着太阳的部分;但当观察者离开这些平面,偏转逐渐能被感到,且日渐增大。在其他情况相同时,当彗尾对于彗星的轨道更倾斜时,偏转较小,且当彗星的头更靠近太阳,尤其是偏转的角取得靠近彗星的头时,亦是如此。此外,没有偏转的彗尾显出是直的,但偏转的彗尾是弯曲的。再者,当偏转大时曲率较大,且在其他情况相同彗尾较长时,感觉更明显,因为在较短的彗尾上曲率不易被观察到。由于偏转的角邻近彗星的头较小,邻近彗尾的另一端较大,且因此彗尾的凸的一侧对着由它形成偏转的方向,并位于从太阳穿过彗星的头所引的无限的直线上。又,彗尾,当它较长且较宽,而又更有力地闪闪发光时,向着凸出的一侧稍微更加明亮且以比凹的一侧较不分明的界线终止。所以,尾部的现象依赖头部的运动,而不是头部被看到的天空的区域;且因此这些现象不是通过天空的折射,而起源于彗星的头所提供的物质。因为如同在我们的空气中,任何被燃烧的物体的烟寻求上升,且如果物体静止时它垂直,或者当物体运动时它倾斜:于是在天空中,当物体有向着太阳的重力,烟和蒸汽应远离太阳上升(正如刚才所说),且如果冒烟的物体静止,则它直线上升;如果物体由于前进总离开蒸汽的部分已上升到的较高的位置,则它倾斜地上升。且当上升的蒸汽较迅速时,倾斜较小,即在太阳附近且靠近冒烟的物体。此外,由于倾斜的参差不齐,蒸汽柱被弯曲;且由于蒸汽到柱向前的一侧稍晚,且因此在同一侧较致密,且所以反射的光更丰富,且边界终止得较不分明。关于彗尾的突然和不稳定的摇动,以及关于它们有时被描述成不规则的形状,在这里我不增加任何东西;因为它们可能起源于我们的空气的变化,以及云的运动,使彗尾的某一部分被遮蔽;或者,也许起源于银河(via lactea)的部分,当彗尾经过时,它可能与它们混淆并被认为是彗尾的部分。
但是能填满如此巨大的空间的蒸汽能来自于彗星的大气,可从我们自己的大气的稀薄上去理解。因为靠近地球的表面的空气所占的一个空间比相同重量的水所占的空间约大850倍,且因此850呎高的圆柱形空气柱与一呎高宽度相同的水柱的重量相同。而且高耸至大气顶端的空气柱,其自身的重量等于高约33呎的水柱;且所以如果整个空气柱的较低的850呎高的部分被除去,剩余的较高的部分自身的重量等于32呎高的水柱。且因此(由被许多实验证实的规则,空气的压力如同压在它们上面的大气的重量,且重力与位置离地球的中心的距离的平方成反比),由第二卷命题XXII的系理计算,我发现,空气,在地球表面之上一个地球的半直径的高度,按照远大于土星轨道之下的整个空间比以一吋的直径画出的球的比稀薄于我们周围的空气。且由是一吋宽的我们的空气充满的球,以在地球的半直径的一个高度上的稀薄度,将充满远至土星的球,甚至更远的区域。因此,由于更高的空气变得极为稀薄,且彗发或者彗星的大气,自那个中心上升到约十倍彗核的表面的高度,然后彗尾从那里上升得更高,彗尾必定极为稀薄。且即使由于更浓密的彗星的大气,和物体向着太阳的大的重力,以及空气和蒸汽的小部分相互之间的重力,在天体的空间中的和在彗尾中的空气可能会不是如此稀薄;然而,从这一计算,显然极少量的空气和蒸汽产生彗尾的所有那些天象是绰绰有余的。因为彗尾的非同寻常的稀薄由星星通过它们发光可推知。地球的大气,厚度只有几哩,被太阳的光照亮时,不仅所有星星的光,而且月球自身的光被遮蔽并熄灭;然而通过极厚的彗尾,它同样地被太阳照亮,能看到最小的星发光,且它们的亮度丝毫不减。大多数的彗尾的亮度通常并不比在暗室中我们的宽度为一吋或者二吋的空气对太阳的光的反射亮。
时间,在此期间蒸汽自彗星的头上升到彗尾的末端,约略可以得知。自彗尾的末端向太阳引一直线,并记下那条直线截[彗星的]轨道的位置。因为,如果蒸汽在一条直线上远离太阳上升,现在它在彗尾的末端,则它一定当彗星的头在相交部分时开始从彗星的头上升。但是由于蒸汽不远离太阳直线上升,蒸汽在上升之前所具有的彗星的运动被保持,而由那个运动和其上升的运动的合成,倾斜地上升。因此问题的解更为接近真实,如果那条直线,它截轨道,画得平行于彗尾的长度[的方向],或者宁可(由于彗星的曲线运动)它偏离彗尾的线。按这种方式我发现,蒸汽,在1月25日它在彗尾的末端,在此前的12月的11日它开始从彗星的头上升,且因此它自身的整个上升用去超过45天的时间。但那整个彗尾出现在12月10日,在过了近日点后两天的时间完成了其上升。所以,蒸汽在邻近太阳时其上升开始得极为迅速,然后以总被其自身的重力迟滞的运动继续上升;且上升增加了彗尾的长度;但彗尾,在能看到的时间,几乎由在彗星过近日点后上升的所有蒸汽组成;且最先上升的蒸汽,组成彗尾的末端,在不是由于彗尾离照亮它的太阳的距离和离我们的眼睛的距离变得太远之前,它不隐没不见。因此,其他彗星的尾,它们不长,也不以迅速和持续的运动自彗星的头上升并不久消失,而是自彗星的头由极缓慢的运动经许多天延长的久留的蒸汽和喷发[形成]的柱,它们,分享彗星的头在蒸汽开始喷发时的那些运动,与彗星的头一起在天空前进。且由此可以推知天体的空间缺乏阻力,因为在它们之中不仅固体的行星和彗星,而且彗尾的极稀薄的蒸汽自由地运动并保持极长的时间。
彗尾从彗星的头的大气上升并在远离太阳的方向上前进被开普勒归之于携带彗尾物质的光束的作用。又,假设在极自由的空间中非常稀薄的气(aura)退让光线的作用,并非绝不相宜,尽管那些光线不能有感觉地移动在我们周围的稠密的物质。另外,有人认为存在如同重力那样的轻力(levitas)的小部分,且彗尾的轻力的物质由于其自身的轻而远离太阳上升。但由于在地球上的物体的重力如同在物体中的物质的量,如果物质的量被保持,既不增加亦不减少,我宁可怀疑这种上升起源于彗尾物质的稀薄作用。在烟囱中的烟由于它飘浮在其中的空气的推动而上升。这些空气,由于热而被稀薄,因为其比重的减小而携带和它缠结的烟一同上升。彗星的尾为何不以同样的方式上升呢?因为太阳的光线对它通过的介质没有作用,除非反射和折射。反射的小部分被此种反射加热,并且小部分把热加于与它们缠结的以太上。那些物质由于传递给它的热而变稀薄,这一稀薄作用使那些物质在被稀薄之前向着太阳的比重被减小,它上升并且携带构成彗尾的反射的小部分。蒸汽的上升也由于它们围绕太阳运行而被增强,而且由这种作用它努力退离太阳,同时太阳的大气和天空的物质或者完全静止,或者仅由从太阳的转动接受到的运动而缓慢地旋转。这些是彗星的尾在太阳的附近上升的原因,在那里轨道更为弯曲,在太阳的稠密的且因此较重的大气内,不久喷射出极长的彗尾。因为彗尾,它们那时被生成,保持自身的运动且同时有朝向太阳的重力,它们在椭圆轨道围绕太阳按照彗星的头的方式运动,且由这种运动,它们总陪伴彗星的头且非常自由地附着在彗星的头上。因为蒸汽向着太阳的重力引起此后彗尾自彗星的头向着太阳的下落不比彗星的头的重力使蒸汽自彗尾的下落来得大。由于它们的公共的重力,它们或者一起落向太阳,或者在它们的上升中一起被迟滞;且因此无论由刚才描述的原因,或者其他任何的原因,那个重力不阻碍彗尾和彗星的头很容易得到的,且此后很容易保持的相互之间的位置。
所以,彗尾,它们产生于彗星的近日点,将与彗星的头一起跑到遥远的区域,无论由此历经多年后与彗星的头一起再回到我们这里,或者在那里被稀薄并逐渐消失。因为后来在彗星的头向太阳降落时,新的、短小的彗尾应以缓慢的运动从彗星的头传播,且那些彗尾当彗星在它们的近日点降低至太阳的大气时,应被无止境地增大。因蒸汽在那些极自由的空间持续变得稀薄并被扩张。由于这个原因所有彗尾在上端比靠近彗星的头更宽。但是被稀薄的蒸汽持续地扩张,最终扩散并分布于整个天空,然后由其重力逐步被吸向行星并与它们的大气混合,看来是适宜的。正如海洋对这个地球的构成是绝对必需的,使得由于太阳的热,丰富的水蒸气出自它们,或者聚积成云,降落为雨,浇灌并滋养整个地球上植物的生长;或者在山顶冷冻凝结(正如一些合理的哲学思索),奔入泉中和河中;因此为了保持海洋和行星上的流体,彗星似乎是需要的,从它们的薄雾和蒸汽的凝结,被植物和腐败作用消耗液体而变干的土地能被不断补充和恢复。因为所有植物全赖液体生长,然后其大部分由腐败作用变为干燥的土地,泥浆持续地从腐败的流体中淤积。因此干地的大小日渐增加,且流体,除非有外来的增加量,必不断减少,直至干涸。再者,我怀疑那种精气(spiritus),它是我们的空气中最小但极精致且最好的部分,而又为万物的生命所需要,主要来自彗星。
只要赫维留对它们的现象的观察是正确的,彗星的大气在它们向太阳降落时由于进入彗尾而被减少,且(无疑对于朝向太阳的那部分)变窄,又在彗星退离太阳时,那时进入彗尾的较少,它又变宽。但是当彗星的头已被加热并射出极大和极亮的尾时,大气层看起来极小,且核被大气包围,它们最低的部分也许是较浓且较黑的烟。因为所有由高热产生的烟一般都是既浓且黑的。因此那颗彗星的头部,我们刚讨论过它,在离太阳和地球相等的距离处,在它经过其近日点之后比在此之前看起来更暗。因在12月它常常可与三等星相比,在11月相当于一等星或者二等星。且那些看到这两者的人把先出现的描述为一颗较大的彗星。因为剑桥的某个青年,在11月19日看到这颗彗星自身的光尽管是铅色的和暗淡的,但等于角宿一,且比后来更亮。11月20日,旧历,蒙塔纳里看到彗星比一等星大,那时[彗尾]的长度为二度。又斯托勒先生,给我们的信中写道,在12月当喷出的尾最大且最亮时,彗星的头不大且所看见的彗星的头的大小远不及彗星在11月日出前所呈现的。且他猜测此事的原因是在开始时彗星的头部的更为丰富的物质已逐渐地被消耗。
其他喷射极大且极亮的尾的彗星,它们的头看起来相当暗淡且微小,这似乎出于相同的原因。因为1668年3月5日,新历,瓦伦廷·斯坦塞尔神父,早上七时,在巴西看见一颗彗星向着太阳下落处的南面,很接近地平线,头极小,几乎看不见,但尾极度明亮,使得站在岸边的人很容易看到它从海中反射的形象。它看起来像自西向南在长度上伸展23度的明亮的火柱,且几乎与地平线平行。但如此大的一个光辉仅持续了三天,之后,马上显著地减小,且在光辉减弱的时间内尾的大小被增加。因此在葡萄牙它被说成几乎占据了天空的四分之一(亦即45度),自西向东以显著的光辉伸展,但不是整个的尾都能被看见,因为在那些部分彗星的头总隐藏在地平线之下。由彗尾的大小的增加和光辉的减小可知,显然彗星的头正退离太阳,且在刚开始被看到时它很靠近太阳,正如1680年的彗星的情形。在《撒克逊编年史》上可以读到,1106年有一颗类似的彗星:星小且暗(如1680年的那颗),然由彼尾发出之光辉亮甚,似火柱伸于东方及北方之间。正如赫维留从达勒姆的僧侣西米恩那里得到的。这颗彗星在2月初出现,且此后在太阳下落处的南方,约在黄昏时能看到。由此且由彗尾的位置推知彗星的头靠近太阳。离太阳之距,帕利斯·马太说,约一肘,自三时(更正确些,六时)至九时,一长光柱由彼射出。这也是亚里士多德在《天象论》第一卷第6节描述过的燃烧的彗星:其头初不能见,或因下沉早于日落,或因匿于日光;次日其形尽现,因距太阳至近,倾即下沉。四散之头火,因(即彗尾)燃烧过度,乃不见。燃烧有日(亚里士多德说),其次乃小,彗星之面目(彗星的头)亦复出现。光辉横天,三有其一(亦即达60gr.)。其所来也,是年(第101次奥林匹克竞技大会的第4年)冬天,其所去也,猎户腰带。1618年的那颗彗星,它从太阳的光线中显示出非常大的尾,似乎等于,甚至于超过一等星,但一些被看到的较大的彗星有较短的尾。传说它们中的一些等于木星,一些等于金星,或者甚至等于月球。
我们说彗星是一类在非常偏心的轨道上围绕太阳运行的行星。且由于行星没有尾,一般地它们之中较小的在靠近太阳的较小的轨道上运行,因此似乎在它们的近日点更靠近太阳的彗星多半较小是合理的,否则因为它们的吸引而对太阳作用太过。但是,至于它们的轨道的横截直径,以及它们运行的循环时间,我留待通过比较过了很长一段时间后又回到相同的轨道的彗星确定它们。同时下面的命题可能有助于此。
命题XLII 问题XXII
修正已求得的彗星的轨道。
运算1 假设由前面的命题发现的轨道的平面的位置;并选择由非常精确的观测确定的彗星的三个位置,且彼此之间的距离尽可能地大,又设A为第一次和第二次观测之间的时间,且B为第二次和第三次观测之间的时间。但在这些位置之一,彗星应在它的近地点,或者至少离近地点不远。由这些视位置,通过三角学运算,发现彗星在假定的那个轨道的平面上的三个真实位置。然后由这些已发现的位置,由算术运算,遵照第一卷命题XXI,围绕作为焦点的太阳的中心,画一圆锥截线;且它的面积,由太阳向所发现的位置引的半径界定,设为D和E;即D为第一次和第二次观测之间的面积,且E为第二次和第三次观测之间的面积。又设T为整个时间,在此期间这颗彗星以由第一卷命题XVI所发现的速度应画出整个面积D+E。
运算2 轨道的平面的交点的黄经被增大,那个黄经加上20′或者30′,它被称为P;且保持那个平面对黄道的平面的倾角。其次从上述的彗星的三个观测到的位置,按照上面,在这个新的平面上发现三个真实位置;再次发现经过那些位置的轨道,且观测之间同样画出的两个面积,是d和e,若整个时间果真为t,在此期间应画出总的面积d+e。
运算3 保持在第一次运算中交点的黄经,而轨道的平面对黄道的平面的倾角被增大,那个倾角加上20′或者30′,它被称为Q。然后从上述观测到的彗星的三个视位置,在这个新的平面上发现三个真实位置;且轨道也穿过那些位置,观察之间同样画出的两个面积,是δ和ε,且整个时间为τ,在此期间应画出总的面积δ+ε。
现在取C比1如同A比B,且G比1如同D比E,又g比1如同d比e,再者γ比1如同δ比ε;再设S为第一次和第三次观测之间的真实时间;且细心观察+号和-号,并按照定律2G-2C=mG-mg+nG-nγ,以及2T-2S等于mT-mt+nT-nτ寻找数m和n。且如果在第一次运算中指定I为轨道的平面对于黄道的平面的倾角,且K为任一交点的黄经,则I+nQ是轨道的平面对黄道的平面的真实倾角,而K+mP为交点的真实黄经。且最终,如果在第一,第二和第三次运算中,指定量R,r和ρ分别为轨道的通径,且量1/L,1/l,1/λ为它们的横截径,则彗星画出的轨道的真实通径为R+mr-mR+nρ-nR,且真实横截径为1/(L+ml-mL+nλ-nL)。从给定的横截径,则彗星的循环时间亦被给定。此即所求。
但是彗星运行的循环时间,以及轨道的横截径,绝不能足够精确地被确定,除非相互比较在不同时期出现的彗星。如果找到几颗彗星,在相等的时间间隔过后,它们画出同一轨道,必须得出所有这些在同一轨道上运行的彗星是一颗且同一颗彗星。且最后由运行时间轨道的横截径被给定,且由这些径椭圆轨道被确定。
所以,为此目的,几颗彗星的轨道的计算依据它们是抛物线的假设。因为这样的轨道总与天象很近似地符合。这是明显的,不仅从1680年彗星的抛物线轨道,在上面我把它与观测相比较;而且也从那颗著名的彗星,它出现在1664年和1665年,且被赫维留观测过。他从自己的观测计算了这颗彗星的黄经和黄纬,但欠精确。由同样的观测,我们的同国人哈雷重新计算了这颗彗星的位置,且由如此发现的位置他确定了彗星的轨道。他发现彗星的升交点在
 21gr..13′.53″,轨道对黄道的平面的倾角为21gr..18′.40″,在其轨道上近日点离交点的距离为49gr..27′.30″。近日点在
21gr..13′.53″,轨道对黄道的平面的倾角为21gr..18′.40″,在其轨道上近日点离交点的距离为49gr..27′.30″。近日点在
 8gr..40′.30″,且日心纬度为南黄纬16gr..1′.45″。彗星在11月伦敦的平时24d.11h.52′的午后,或者格但斯克的13h.8′,旧历,在近日点,且抛物线的通径为410286,地球离太阳的平均距离取作100000。在这一计算的轨道上彗星的位置与观测符合得何等精确,从如下由哈雷计算的表显而易见。
8gr..40′.30″,且日心纬度为南黄纬16gr..1′.45″。彗星在11月伦敦的平时24d.11h.52′的午后,或者格但斯克的13h.8′,旧历,在近日点,且抛物线的通径为410286,地球离太阳的平均距离取作100000。在这一计算的轨道上彗星的位置与观测符合得何等精确,从如下由哈雷计算的表显而易见。
1665年初的2月,白羊座的第一颗星,今后我称之为γ,在
 28gr..30′.15″,且北黄纬为7gr..8′.58″。白羊座的第二颗星在
28gr..30′.15″,且北黄纬为7gr..8′.58″。白羊座的第二颗星在
 29gr..17′.18″,且北黄纬为8gr..28′.16″。又[座中的]一颗七等星,我称之为A,在
29gr..17′.18″,且北黄纬为8gr..28′.16″。又[座中的]一颗七等星,我称之为A,在
 28gr..24′.45″,且北黄纬为8gr..28′.33″。在巴黎的2月7d.7h.30′(亦即格但斯克的2月7d.8h.37′),旧历,彗星与星γ和A构成一三角形,直角在γ。且彗星离星γ的距离等于星γ和星A之间的距离,亦即一个大圆的1gr..19′.46″;且因此在星γ的纬线的平行线上是1gr..20′.26″。所以,如果从星γ的黄经除去经度1gr..20′.26″,留下彗星的黄经
28gr..24′.45″,且北黄纬为8gr..28′.33″。在巴黎的2月7d.7h.30′(亦即格但斯克的2月7d.8h.37′),旧历,彗星与星γ和A构成一三角形,直角在γ。且彗星离星γ的距离等于星γ和星A之间的距离,亦即一个大圆的1gr..19′.46″;且因此在星γ的纬线的平行线上是1gr..20′.26″。所以,如果从星γ的黄经除去经度1gr..20′.26″,留下彗星的黄经
 27gr..9′.49″。奥祖,从他自己的这一观测中近似地把彗星置于
27gr..9′.49″。奥祖,从他自己的这一观测中近似地把彗星置于
 27gr..0′。从胡克描绘的彗星的运动图中,那时它在
27gr..0′。从胡克描绘的彗星的运动图中,那时它在
 26gr..59′.24″。取平均值,我把它置于
26gr..59′.24″。取平均值,我把它置于
 27gr..4′.46″。由相同的观测,奥祖把彗星当时的黄纬置为向北7gr.又4′或者5′。他本应该把它置于更准确的7gr..3′.29″,因为彗星的和星γ的黄纬的差等于星γ和星A的黄经的差。
27gr..4′.46″。由相同的观测,奥祖把彗星当时的黄纬置为向北7gr.又4′或者5′。他本应该把它置于更准确的7gr..3′.29″,因为彗星的和星γ的黄纬的差等于星γ和星A的黄经的差。
伦敦的2月22d.7h.30′,亦即格但斯克的2月22d.8h.46′,根据胡克的观测,他自己画在一幅图中,以及奥祖的观测,并由珀蒂画在一幅图中,彗星离星A的距离,是星A和白羊座的第一颗星之间的距离的五分之一,或者15′.17″。且彗星离连结星A和白羊座的第一颗星的线的距离是同一个五分之一的四分之一,亦即4′。且因此彗星在
 28gr..29′.46″,且北黄纬为8gr..12′.36″。
28gr..29′.46″,且北黄纬为8gr..12′.36″。
伦敦的3月1d.7h.0′,亦即格但斯克的3月1d.8h.16′,彗星被观测到靠近白羊座的第二颗星,它们之间的距离比白羊座的第一和第二颗星之间的距离,这就是,比1gr..33′,如同4比45,按照胡克;或者如同2比23,按照戈蒂尼。因此彗星和白羊座第二颗星之间的距离,按照胡克为8′.16″,按照戈蒂尼为8′.5″,或者取平均,为8′.10″。又按照戈蒂尼,彗星现在刚过了白羊座的第二颗星大约它一天完成的空间的四分之一或者五分之一,亦即大约1′.35″(对此奥祖深表同意),或者按照胡克稍小一些,他置之为1′。所以,如果白羊座的第一颗星的黄经加上1′,且其黄纬加上8′.10″,得到彗星的黄经
 29gr..18′,且北黄纬8gr..36′.26″。
29gr..18′,且北黄纬8gr..36′.26″。
巴黎的3月7d.7h.30′(亦即格但斯克的3月7d.8h.37′),由奥祖的观测,彗星离白羊座第二颗星的距离等于白羊座第二颗星离星A的距离,亦即52′.29″。且彗星的和白羊座第二颗星的黄经的差为45′或者46′,或者取平均45′.30″。且因此彗星在
 0gr..2′.48″。由奥祖的观测图,它由珀蒂绘制,赫维留导出彗星的黄纬为8gr..54′。但刻工使彗星临近其运动结束时的路径不合法地弯曲,而赫维留在奥祖的观测图上由自己作图纠正了不合法的弯曲,且如此彗星的黄纬成为8gr..55′.30″。且由稍大一点的纠正,黄纬成为8gr..56′或者8gr..57′。
0gr..2′.48″。由奥祖的观测图,它由珀蒂绘制,赫维留导出彗星的黄纬为8gr..54′。但刻工使彗星临近其运动结束时的路径不合法地弯曲,而赫维留在奥祖的观测图上由自己作图纠正了不合法的弯曲,且如此彗星的黄纬成为8gr..55′.30″。且由稍大一点的纠正,黄纬成为8gr..56′或者8gr..57′。
3月9日,这颗彗星亦曾被看到,且那时它的位置应在
 0gr..18′,且北黄纬约为9gr..
0gr..18′,且北黄纬约为9gr..
 ′。
′。
这颗彗星在三个月内可以见到,它几乎行经六个宫,且其中有一天几乎完成约二十度。它的路径与一个极大的圆偏离很多,路径向北弯曲;且其运动临近结束时由逆行变为顺行。而尽管其路径如此异常,自始至终理论与观测符合的精确性,不低于通常行星的理论与对它们的观测的符合,由表这是明显的。但我们在彗星最迅速时,应减去约二分,这使得从升交点和近日点之间的角被除去十二秒,或者使那个角为49gr..27′.18″。两颗(这一颗和前面的一颗)彗星中每一颗的周年视差很显著,且由此地球在大轨道上的周年运动被证明。
此理论亦被一颗彗星的运动证实,它出现在1683年。这颗彗星在一条轨道上逆行,它的平面与黄道的平面几乎夹一直角。它的升交点(由哈雷的计算)在
 23gr..23′;轨道对黄道的平面的倾角为83gr..11′;近日点在
23gr..23′;轨道对黄道的平面的倾角为83gr..11′;近日点在
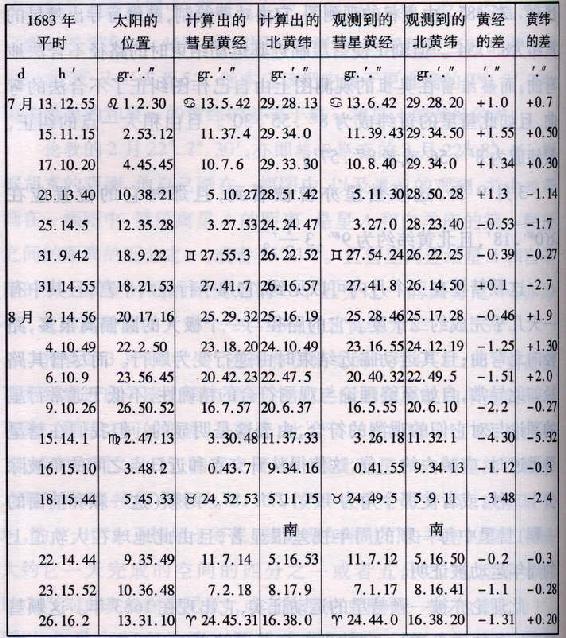
 25gr..29′.30″;近日点离太阳的距离为56020,大轨道的半径取作100000,且它在近日点的时间为7月2d.3h.50′。又彗星在这一轨道上的位置由哈雷计算,并与弗拉姆斯蒂德观测到的位置相比较,如下表所示。
25gr..29′.30″;近日点离太阳的距离为56020,大轨道的半径取作100000,且它在近日点的时间为7月2d.3h.50′。又彗星在这一轨道上的位置由哈雷计算,并与弗拉姆斯蒂德观测到的位置相比较,如下表所示。
理论也被一颗逆行的彗星的运动证实,它出现在1682年。它的升交点(由哈雷的计算)在
 21gr..16′.30″。轨道对黄道的平面的倾角为17gr..56′.0″。近日点在
21gr..16′.30″。轨道对黄道的平面的倾角为17gr..56′.0″。近日点在
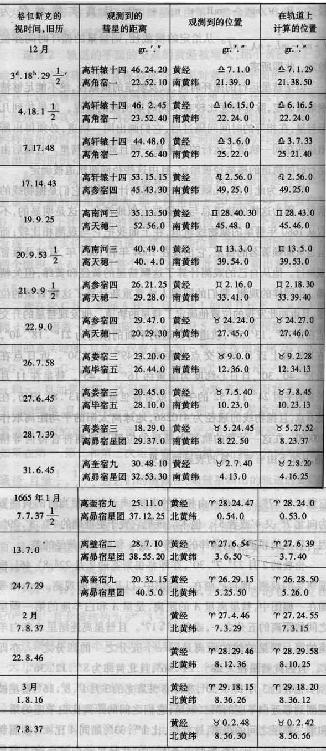
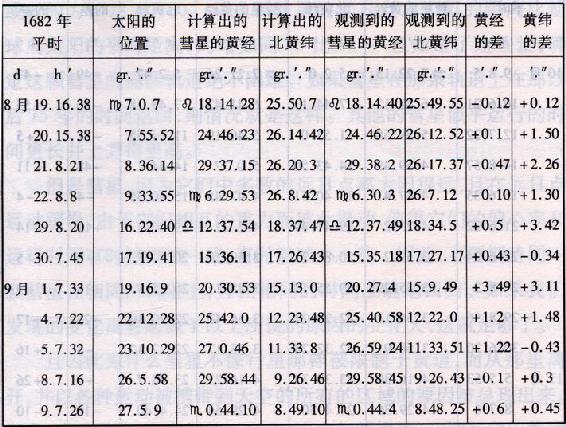
 2gr..52′.50″。近日点离太阳的距离为58328,大轨道的半径取为100000。且它在近日点的平时为9月4d.7h.39′。由弗拉姆斯蒂德的观测计算的位置与由理论计算的位置的比较,如下表所示。
2gr..52′.50″。近日点离太阳的距离为58328,大轨道的半径取为100000。且它在近日点的平时为9月4d.7h.39′。由弗拉姆斯蒂德的观测计算的位置与由理论计算的位置的比较,如下表所示。
理论又被一颗逆行的彗星的运动证实,它出现在1723年。这颗彗星的升交点(由牛津的萨维里天文学教授布拉得雷先生的计算),在
 14gr..16′。轨道对黄道的平面的倾角为49gr..59′。近日点在
14gr..16′。轨道对黄道的平面的倾角为49gr..59′。近日点在
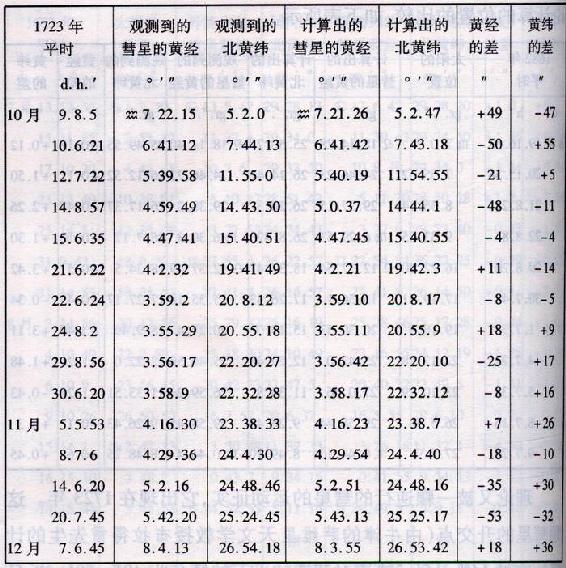
 12gr..15′.20″。近日点离太阳的距离为998651,大轨道的半径取为1000000,且它在近日点的平时为9月16d.16h.10′。彗星在这一轨道上的位置由布拉得雷计算,且与由他自己和由他的舅父庞德先生,以及由哈雷先生观测的位置的比较,如下表所示。
12gr..15′.20″。近日点离太阳的距离为998651,大轨道的半径取为1000000,且它在近日点的平时为9月16d.16h.10′。彗星在这一轨道上的位置由布拉得雷计算,且与由他自己和由他的舅父庞德先生,以及由哈雷先生观测的位置的比较,如下表所示。
由这些例子更为清楚,彗星的运动由我们阐述的理论表示,在精确性上并不比通常由行星的理论表示行星的运动差。且所以彗星的轨道能由这一理论计算,而彗星在任意的轨道上运行的循环时间终究能被确定,且最后椭圆轨道的横截径和远日点的高度会被知道。
一颗逆行的彗星,它出现在1607年,画出一条轨道,它的升交点(由哈雷的计算)在
 20gr..21′;轨道的平面对黄道的平面的倾角为17gr..2′;近日点在
20gr..21′;轨道的平面对黄道的平面的倾角为17gr..2′;近日点在
 2gr..16′;且近日点离太阳的距离为58680,大轨道的半径取为100000。又彗星在10月16d.3h.50′在近日点。这一条轨道与出现在1682年的一颗彗星的轨道非常接近。如果这两颗彗星是一颗且同一颗,则这颗彗星的运行时间为75年,且它的轨道的长轴比大轨道的长轴,如同√c:75×75比1,或者约为1778比100。又这颗彗星的远日点离太阳的距离比地球离太阳的平均距离,约略如同35比1。一旦知道了这些量,确定这颗彗星的椭圆轨道绝不困难。如果彗星在那条轨道上在那以后75年的时间返回,则情况就是这样。其他的彗星似乎运行的时间更长并上升得更高。
2gr..16′;且近日点离太阳的距离为58680,大轨道的半径取为100000。又彗星在10月16d.3h.50′在近日点。这一条轨道与出现在1682年的一颗彗星的轨道非常接近。如果这两颗彗星是一颗且同一颗,则这颗彗星的运行时间为75年,且它的轨道的长轴比大轨道的长轴,如同√c:75×75比1,或者约为1778比100。又这颗彗星的远日点离太阳的距离比地球离太阳的平均距离,约略如同35比1。一旦知道了这些量,确定这颗彗星的椭圆轨道绝不困难。如果彗星在那条轨道上在那以后75年的时间返回,则情况就是这样。其他的彗星似乎运行的时间更长并上升得更高。
但是彗星,因为它们中多数的远日点离太阳很远,且在远日点运动缓慢,由于它们相互的重力而彼此摄动,使得它们的偏心率和运行时间有时被增加一些,有时被减小一些。因此,不要期待同一颗彗星在相同的轨道上,且在相同的时间准确地回归。如果我们发现的变化没有起源于以上所说的原因的变化大,这就足够了。
且因此为什么彗星不像行星那样被限制于黄道,而从那里离开,并以各种运动被携带到天空的所有的区域的原因被显现出来。即是,为此目的,在它们的远日点,当它们缓慢地运动时,它们能彼此离得尽可能地远且彼此之间的牵引尽可能地小。这是彗星下降至最低,且因此在远日点远动得最慢,并也应该升至最高的原因。
一颗彗星,它出现在1680年,在它自己的近日点离太阳的距离小于太阳的直径的六分之一;且由于它的速度在接近太阳的那个地方最大,又由于一定的太阳的大气的密度,彗星必定受到一些阻碍和迟滞,因此经每次运行更靠近太阳,并最终落到太阳的本体上。但是在它的远日点,当它运动得最缓慢时,有时会由于其他彗星的吸引而有些被迟滞,且因此向太阳降落。恒星也是如此,它们逐渐发出光和蒸汽,能由彗星落入它们而得以补给,且被它们的新的供给点燃,而被认为是一颗新星。这一类的那些恒星,它们突然出现,起初以极大的光辉发亮,且以后逐渐消失。在仙后座的椅上出现的就是如此的一颗星,1572年11月8日,当科内利乌斯·格马在天气晴朗的晚上巡视那一部分天空时,一点也看不到它;在次日(11月9日)晚上,他看见它比任何恒星都亮,且其光辉难于让位于金星。第谷·布拉赫在同一个月的11日,当这颗星最亮时看到了;并且他观察到自那时以后它逐渐减弱,又在16个月的时间之后,他观察到它的消失。在11月,当它刚出现时,它的光辉等于金星。在12月,它减小一些,等于木星。在1573年的1月,它弱于木星而比天狼星(sirius)亮,在2月和3月初它变得等于天狼星。在4月和5月被看到等于二等星,在6月、7月和8月等于三等星,在9月、10月和11月等于四等星,在12月和1574年的1月等于五等星;且在2月被看到等于六等星,又在3月它飘然而逝。它的颜色在开始时明朗、发白且发亮,此后变黄,且在1573年3月它像火星和毕宿五(Aldebaran)那样发红;但在5月它呈青白色,如我们在土星上看到的,它保持这种颜色直至最后,然而一直在变暗。这类星也出现在蛇夫座的右脚,在1604年9月30日,旧历,它开始被开普勒的学生们观察到,且其光辉超过木星,而在前一夜,一点也看不到它,且自那时起它逐步减弱,在15或者16个月的时间飘然而逝。据说以不寻常的光辉按这种方式出现的一颗新星唤起喜帕恰斯去观测恒星并列为星表。但是恒星,它们交替地出现并消失,也逐渐增大,但它们自身的光辉很少超过三等星,它们似乎是另一类的星,且由旋转交替显示明的一侧和暗的一侧。但是蒸汽,它们起源于太阳和恒星,以及彗星的尾,由自身的重力它们能落入行星的大气中,且在那里凝结并变成水和湿气(spiritus
humidos),且之后由于缓热逐渐变成盐、硫黄、酊(tinctura)、泥、黏土、陶土、沙、石、珊瑚,以及其他地上的物质。
总释(SCHOLIUM GENERALE)
涡漩的假设被许多困难包围。由于任意行星向太阳所引的半径画出的面积与时间成比例,涡漩的部分的循环时间应按照离太阳的距离的二次比。由于行星的循环时间按照离太阳的距离的二分之三次比,涡漩的部分的循环时间必须按照距离的二分之三次比。由于围绕土星、木星和其他行星的较小的涡漩保持旋转且平静地漂浮在太阳的涡漩中,太阳的涡漩的部分的循环时间应相等。太阳和行星围绕它们自身的轴旋转,它们应与涡漩的运动相符,这与所有所说的比例不相容。彗星的运动是极为规则的,且遵从与行星运动相同的定律,而这不能由涡漩解释。彗星以很大的偏心运动被携带到天空的所有部分,这是不可能的,除非涡漩被除去。
抛射体,在我们的空气中,只受到空气的阻碍。抽出空气,如同在波义耳的真空中,阻力消失,诚然如此,则纤细的羽毛和纯金以相同的速度在这真空中下落。且这对天上的空间,它在地球的大气之上,有相同之理。所有物体在这种空间中应自由地运动;且所以行星和彗星在种类和位置被给定的轨道上按前面阐述过的定律永久地运行。无疑它们由重力的定律被保持在自己的轨道上,但绝不能由这些定律在一开始就获得轨道的规则的位置。
六个一等行星围绕太阳在太阳的同心圆上运行,运动的方向相同,很近似地在同一平面上。十个月球围绕地球,木星和土星在它们的同心圆上运行,运动的方向相同,很近似地在行星轨道的平面上。而所有这些规则的运动不起源于力学的原因;因为彗星在偏心率很大的轨道上,被自由地携带到天空的所有部分。以这种类型的运动,彗星极迅速且极容易地穿过行星的轨道,且在它们自己的远日点,在那里它们很缓慢地运动且逗留很长时间,它们彼此相距非常遥远,使得相互的牵引尽可能地小。太阳、行星和彗星的这个极精致的结构不可能发生,除非通过一个理智的和有权能的存在(ens)的设计和主宰。且如果恒星位于类似的系统的中心,所有这些,因为是根据类似的设计建造的,必定受惟一者的主宰;尤其是由于恒星的光与太阳的光的本性相同,且每一个系统的光向其他所有系统发射,且为了使恒星的系统不因为它们自身的重力而相互降落,他让它们彼此之间存在巨大的距离。
他不是作为宇宙的灵魂,而是作为一切的主宰而统治所有。且a亦即宇宙的统帅。因为他自身的统治,我主上帝经常被称作aΠαντοκρáτωρ,因为上帝是一个相对的称谓,且涉及臣仆;再者神性是上帝的统治权,不是对其自身的本体,如上帝是宇宙的灵魂的那个看法,而是对臣仆。至高的上帝是永恒的、无限的、绝对完美的存在;但无论如何,一个完美却没有统治权的存在不是我主上帝。我们也说我的上帝,你们的上帝,以色列人的上帝,上帝的上帝,以及主人的主人,但我们不说我的永恒者,你们的永恒者,以色列人的永恒者,上帝的永恒者;我们不说我的无限者,或者我的完美者。这些称号不包含对臣仆的关系。上帝b我国人波科克从阿拉伯语的词du(在间接格的情形:di)引出[拉丁文的]词dei,它的意思是主人。且在这种意义上王子被称为dii,《诗篇》lxxxiv.6和《约翰福音》x.45。以及摩西被称为他哥哥亚伦的上帝,法老的上帝(《出埃及记》iv.16和vii.1)。且在相同的意义上过去死了的王子的灵魂被异教徒称为上帝,但这是错误的,由于他们缺乏统治权。这个词处处指主人,但并非每个主人是上帝。精神存在的统治权构成上帝,真正的统治权构成真正的上帝,崇高的统治权构成崇高的上帝,想象上的统治权构成想象上的上帝。且作为出自真正的统治权的结果,真正的上帝是生气勃勃的、明智的和有权能的;从其余的完美性上来说,他是至高者或者最高的完美。永恒者(æternus)是无限的、全能的和全知的,亦即,在自无有穷期到无有穷期的延展中,在从无限到无限的空间中,他统治一切;且他知道一切,无论是已发生的和将要发生的。他不是永恒和无限,而是永恒的和无限的;他不是持续(duratio)和空间(spatium),而是持续的和此在的,他永恒持续,且无所不在,且通过他永久的和到处的存在,构成持续和空间。由于空间的每一个小部分是永久的,且持续的任一不可分的瞬是无处不在的,毫无疑义,万物的创造者和主人是无时不在的和无处不在的。每一个有感觉的灵魂,在不同的时间,且在不同的感觉的和运动的器官上,是同一个不可分的主体(persona)。给定的部分在持续上是连续的,在空间上是共存的,二者皆不在人的主体中或者他的思维本原中;且更不在上帝的思维实体中。每一个人,就感觉问题而言,是一个,且同一个在他自己生命延续期间存在于所有和每个感觉器官中的人。上帝是一个且同一个永恒的和无处不在的上帝。他无处不在不仅由其能力,而且也由其实质:因为无实质无以支持能力。一切事物被他c这是古人的看法,如西塞罗在《论上帝的本性》第I卷中的毕达格拉斯。泰勒斯,阿那克萨哥拉,维吉尔《农事诗》第iv卷,第220行,和《伊尼特》第6卷721行;斐洛在《寓言》第I卷的开头;阿拉托斯在《天象》的开头。这也是圣书作者的看法,如保罗在《使徒行传》xvii.27,28。约翰在《约翰福音》xiv.2。摩西在《出埃及记》iv.39以及x.14。大卫在《诗篇》cxxxix.7,8,9。所罗门在《列王记·上》viii.27。约伯在《约伯记》xxii.12,13,14。耶利米在《耶利米书》xxiii.23,24。此外,偶像崇拜者想象太阳,月球和星星,人的灵魂以及世界的其他部分是至高的上帝的部分,且因此但却是错误地加以崇拜。包容且在其中运动,但没有相互的感觉。上帝不承担来自躯体的运动;那些躯体丝毫没有感到来自上帝的无处不在的阻碍。承认至高上帝的存在是必然的,且同样要承认他是永恒的和无处不在的。因此他也完全与自身相似,全都是眼,全都是耳,全都是脑,全都是臂,全都是感觉的、理解的和作用的力,但绝不以人的方式,绝不以物体的方式,总起来以我们不能理解的方式[存在]。正如失明者没有颜色的概念,我们同样没有一种方式,以它能完全感觉和理解最明智的上帝。他完全离弃了身体和身体的外形,且因此既不能被看到,也不能被听到,也不能被触到,也不应以某一身体形象加以礼拜。我们有他的属性的观念,但我们对任一事物的本质一无所知。我们看到的只是物体的形状和颜色,听到的只是声音,触到的只是[物体的]外表,嗅到的仅仅是气味,尝到的只是滋味:对最深的本质我们没有感觉,也不能认识它们反映的行动;且我们更不能对上帝的本质有什么概念。我们只能通过他的性质和品质,并通过至慧和至善的事物的结构和终极原因认识他,且由于他的完美性而钦佩他;又由于统治权而崇拜和服务于他。我们的服务也是作为臣仆,且没有统治权,先见的和终极目的的上帝除命运和大自然外什么也不是。由形而上学的盲目的必然性,无论如何它同样是永恒的和无处不在的,但事物的变化不可能由它产生。一切事物在位置和时间状况上的差异,只可能出自一个真的必然存在的理念(idea)和意志。但人们通过寓言说上帝能看,能听,能说,能笑,能爱,能恨,能慕,能予,能受,能喜,能怒,能战,能制,能立,能建。因为所有关于上帝的说法借用了出自人的关系的某种程度的相似性,这种相似性不是完美的,但能达到一定程度。关于上帝而言就是这些,从现象研究他,从属于自然哲学。
到现在为止,我由重力解释了天体的和我们的大海的现象,但我尚未指明重力的原因。无疑,这种力起源于某个原因,它深入到太阳的和行星的中心,能力没有减小;且那种作用不与它在其上作用(如通常力学的原因)的表面上的小部分的量成比例,而与立体中的物质的量成比例,且其作用在每个方向被延伸到巨大的距离,总按照距离的二次比减小。向着太阳的重力由向着太阳的每个小部分的重力复合而成,且在退离太阳时精确地按照距离的二次比减小直至土星的轨道,由行星的远日点静止,这是显然的,且甚至一直到彗星最远的远日点,只要那些远日点静止。我尚未能从现象导出重力的这些性质的原因,且我不虚构假设(hypotheses non fingo)。因为凡不能现象导出的,被称为假设;且假设,无论是形而上学的,或者是物理学的,无论是隐藏的属性的,或者是力学的,在实验哲学中是没有地位的。在这一哲学中,命题由现象导出,且由归纳法使之一般化。物体的不可入性,可运动性,和冲击以及运动的和重力的定律就是如此被发现的。且重力确实存在,并按照我们已阐述的定律作用,由它足以解释天体和我们的海洋的一切运动,这就够了。
现在有可能增添关于某种气(spiritus)的一些内容,它极为精细,能侵入粗大物体并藏匿在它们之中;由它的力和作用,物体的小部分在极短的距离相互吸引,且当它们接触时凝聚;且带电的物体在较远的距离作用,排斥并吸引邻近的小物体;此外,光被发射,反射,折射,弯曲,并加热物体;且所有被激起的感觉,以及动物的肢体按意愿的要求运动,即,由这种气的振动,沿着神经的牢固的纤维从外部的感觉器官传播到脑,再由脑传入肌肉。但这些事情三言两语说不清楚;而且没有足够多的实验,由它们能精确地确定和证明这种气的作用定律。