第四章 米西斯—莱新巴哈的频率说
两个当时住在君士坦丁的德国教授所写的两本重要的书以不同于上章所用的方式提出了关于概率的频率解释。[6]
莱新巴哈的著作是米西斯著作的发展,在各个方面都是同一理论的更好的说明。因此我将只讨论莱新巴哈的著作。
莱新巴哈在列举出概率计算的公理之后,他就提出一种看来是由于见到统计上的相互关联而想出的解释。他假定两个级数(x1,x2,……xn,……),(y1,y2,……yn,……),以及O和P两个类。有些x或者所有x属于O类;莱新巴哈感兴趣的问题是:与x相对应的y属于P类的频率是多少?
举例来说,假定你在研究一位丈夫是否因为他的太太唠叨不休而想自杀的问题。就这个事例来说,x都是妻子,y都是丈夫,O类由唠叨不休的人组成,P类由自杀的人组成。然后已知一个妻子属于O类,我们的问题是:她的丈夫属于P类的频率是多少?
让我们看一看两个系列中各自由前n项组成的部分。假定在前n个x当中,有a项属于O类,并且假定这些当中有b项使得与x相对应的y属于P类。(与x相对应的y和x具有相同的下标。)这样我们说在从x1到xn的整个部分中O和P的“相对频率”是b/a。[如果所有x都属于O类,那么a=n,而相对频率就是b/n。]我们用“Hn(O,P)”来表示这种相对频率。
我们现在进一步给“P在已知O的条件下的概率”下定义,这个概率我们用“W(O,P)”来表示。这个定义是:W(O,P)是当n无限增大时Hn(O,P)的极限。
我们使用一点数理逻辑就可以使这个定义大大简化。首先,两个系列是不必要的。因为我们假定两个系列都是级数,因而在它们的项目之间存在着某种构成一一对应关系的东西。如果这叫作S,那么说某一个y属于一个P类就等于说与它对应的x属于那个由对于P的分子当中某一个分子具有S关系的项目所组成的类。例如,设S是妻子对于丈夫的关系;如果y是一个结过婚的人,并且x是他的妻子,那么y是一个政府官员这句话在并且只有在x是一个政府官员的妻子的情况下才为真。
其次,承认不是所有的x都属于O类这种情况并没有什么好处。这个定义只有在无限数目的x属于O类的情况下才是适当的;在这种情况下,那些属于O类的x形成一个级数,而我们就可以把其他剩下的部分忘记。这样如果我们换用下面的说法,我们就把莱新巴哈的定义中最重要的部分保留下来:
设Q为一个级数,a是某个类,就a当中重要的实例来说,在Q这个系列中存在着比任何已知分子还要靠后的分子。设m为α的分子在Q的前n个分子当中的数目。那么我们把W(Q,α)定义为当n无限增大时m/n的极限。
也许是由于疏忽,从莱新巴哈的说法来看,好像概率的概念只适用于级数,而完全不适用于有限类。我认为这并不是他的本意。举例来说,人类是一个有限类,并且我们愿意在生死统计上使用概率,而完全按照定义的说法是不能做到这一点的。作为一件心理事实来看,当莱新巴哈说到n=无限大时的极限的时候,他是把极限当作某个只要在n从经验观点上看是大的情况下就可以非常接近的数,即是说只要在n与我们的观察手段所能达到的最大限度相距不远的情况下。他有一个公理或者公设,意思是说就每个大的可以观察的n来说,如果存在着这样一个数,那么它就接近等于n=无限大时的极限。这是一个很别扭的定义,不仅因为它是随意规定的,而且还因为我们所研究的纯粹数学范围以外的大多数系列都不是无限系列;我们确实可以怀疑它们当中任何一个是否存在。我们习惯于假定时空是连续的,这就蕴涵着无限系列的存在;但是这种假定除了为了数学上的方便而外是没有任何基础的。
为了使莱新巴哈的理论变得尽可能适用,我将假定就有限系列的范围而论,上一章所给的定义可以保留,而新的定义只是为了使我们能把概率用于无限系列而作的一种扩充。这样他的Hn(O,P)就将是一种概率,但却是一种只能应用于系列的前n项的概率。
作为他的归纳形式,莱新巴哈假定了大体如下的公设:假定我们已经对于O和P的相互关联作过N次观察,使得我们对于直到n=N为止所有n的值都能计算出Hn(O,P),并且假定对于整个后一半n的值来说,Hn(O,P)与某一分数P相差永远小于ε,这里ε是很小的数。然后我们将假定不管我们怎样增大n,Hn(O,P)将仍然不超出这些狭窄的界限,因而作为n=无限大时的极限的W(O,P)也不会超出这些界限。如果没有这个假定,关于n=无限时的极限我们也就不会有任何经验上的证据,而专为了它们才作出这个定义的那些概率也就一定完全不能被人认识。
面对着上面所说的困难,人们可以为莱新巴哈的理论提出两点辩护理由。第一,他可能认为假定n无限接近无限大并不必要;就所有实际用途来说,只要n可以变得非常大就够了。比方说假定我们在研究生死统计。保险公司并不关心再过一万年之后生死统计上所发生的变化;它所关心的最多不过是今后一百年的事。在我们已经积累统计结果之后,如果我们假定直到我们掌握了十倍于目前的数据之前,频率将大体保持不变,这就足以应付所有实际的需要。莱新巴哈可能说当他说到无限大时,他用的是一种方便的数学速记,意思只表示“这个系列中我们一直还没有研究过的一大部分”。他也许说,这种情况极其类似用经验方法确定速度的情况。从理论上讲,一个速度只有在可测量的空间和时间的微小性没有限度的条件下才可以确定;从实用上讲,因为不存在这样的极限,我们也就从来不能知道在一个瞬间哪怕是近似的速度。诚然我们可以相当准确地知道一小段时间内的平均速度。但是即使我们假定连续性的公设,通过比方说一秒钟的平均速度我们也绝对得不到关于这一秒钟的一个特定瞬间的速度的任何知识。一切运动也许可能都是由为一些无限速度的瞬间所隔开的静止时间所组成的。如果我们不依靠这种极端的假说,即使我们假定数学意义上的连续性,任何一个瞬间的有限速度都可以与一段一定时间内任何有限平均速度不相抵触,不管包括这个瞬间的这段有限时间怎样短暂。可是就实际用途来说,这并没有什么关系。除了类似爆炸的少数现象外,如果我们认为通过一段很短可测量时间所得到的任何瞬间速度近似于那段时间的平均速度,那么我们就会发现物理学的定律是能够证实的。因此我们可以把“瞬间速度”当作为了方便而想出来的数学上的虚构。
同样,莱新巴哈可能说,当他说到在n为无限时一个频率的极限的时候,他所指的只是在很大的数目下实际的频率,或者不如说具有很小限度误差的这种频率。无限大和无限小是同样不能观察的,因而(他可能说)对于经验科学来说是同样无关宏旨的。
我愿意承认这个答案的正确性。我只因为莱新巴哈的书没有明确地把这一点讲出来而感到惋惜;但是我却认为他心里一定是这样想的。
有利于他的学说的第二个论点就是它正好适用于我们愿意对之应用概率论证的那些实例。当我们关于某一将来事件具有某些数据,但却不足以确定这个事件在我们感兴趣的方面所具有的特性时,我们就愿意使用这些论证。比方说,我的死亡是一个将来的事件,并且如果我去保寿险,我就可能想知道关于我可能死在某一特定年份存在着什么证据。就这样的实例来说,我们总有许多记录在一个系列中的个别事实,并且我们假定我们迄今所发现的那些频率将大体继续下去。或者举赌博为例,这是全部概率产生的来源。我们感兴趣的并不是一次掷两个骰子有36种可能的结果这个单纯的事实。我们感兴趣的是这件事实(如果它是事实的话),即在由拋掷组成的一个很长的系列中,这36种可能当中每一种可能都有近似相等的实现次数。这是一件不能仅从36种可能的存在推论出来的事实。当你遇到一个生人的时候,恰好有着两种可能:一方面,他可能是埃本尼兹·威尔克斯·史密斯;另一方面,他可能不是。但是在我漫长的一生中,我遇到过许多生人,我发现前一种只实现过一次。纯粹数学中的概率论只列举可能的事例,除非我们知道每种可能的事例发生的频率近似相等,或者以某种已知频率发生,否则这种理论就没有实用上的好处。如果我们研究的是事件,而不是一个逻辑图式,那就只能通过实际统计才能知道,而我们可以说实际统计的应用一定要大体按照莱新巴哈的理论来进行。
我也将只是暂时承认这种论证;将来我们考察归纳的时候,我们将重新研究这种论证。
对于照莱新巴哈所讲的那种理论还有另外一种不同性质的反对意见,这种意见所针对的是他在似乎只需要类的情况下引入了级数。让我们举一个具体的例子来说明:任意选取的一个整数是质数的机会有多少?如果我们按照整数的自然顺序来选取整数,那么照他的定义来说,机会是零;因为如果n是一个整数,在n为大数时,小于或等于n的质数的数目近似于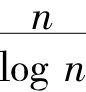 ,所以一个小于n的整数为质数的机会近似于
,所以一个小于n的整数为质数的机会近似于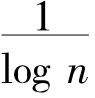 ,而在n无限增大时
,而在n无限增大时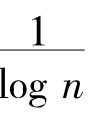 的极限为零。但是现在假定我们按照下面的方式重新排列整数:先排好前9个质数,然后排上第一个不是质数的数,再排好下9个质数,然后排上第二个不是质数的数,这样一直无限地排下去。当整数按照这种顺序排好之后,莱新巴哈的定义表明任意选取的一个数目为质数的机会是9/10。我们甚至能把整数安排得使一个数目不为质数的机会为零。为了得到这个结果,先排第一个非质数——即4——然后再在第n个非质数的后面排上已经排好的质数以后的n个质数;这个级数的开始是:4,1,6,2,3,8,5,7,11,9,13,17,19,23,10,29,31,37,41,43,12,……。在这个排列中,在第(n+1)个非质数之前将有n个非质数和
的极限为零。但是现在假定我们按照下面的方式重新排列整数:先排好前9个质数,然后排上第一个不是质数的数,再排好下9个质数,然后排上第二个不是质数的数,这样一直无限地排下去。当整数按照这种顺序排好之后,莱新巴哈的定义表明任意选取的一个数目为质数的机会是9/10。我们甚至能把整数安排得使一个数目不为质数的机会为零。为了得到这个结果,先排第一个非质数——即4——然后再在第n个非质数的后面排上已经排好的质数以后的n个质数;这个级数的开始是:4,1,6,2,3,8,5,7,11,9,13,17,19,23,10,29,31,37,41,43,12,……。在这个排列中,在第(n+1)个非质数之前将有n个非质数和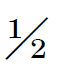 n(n+1)个质数;这样随着n的增大,非质数的数目与质数的数目之比就趋近于0,而以0为极限。
n(n+1)个质数;这样随着n的增大,非质数的数目与质数的数目之比就趋近于0,而以0为极限。
从这个具体例子来看,显然如果我们接受莱新巴哈的定义,同时已知任何一个具有与自然数项数相同的类A,并且已知任何一个无限子类B,那么一个任意选取的A为一个B的机会将为0到1之间的任何数(包括0和1在内),这要看我们选择的把B分配在A中的方式来决定。
由此可以看出,如果要把概率应用到无限集合上来,它一定适用于级数而不适用于类。这一点看来似乎有些奇怪。
诚然,就经验界的数据来讲,这些数据都是按照时间顺序出现的,因而也就构成一个系列。如果我们愿意假定将有无限多个我们正在研究的那种事件出现,那么我们也能确定我们的概率定义只适用于按照时间序列排好的事件。但是在纯粹数学的范围之外,我们还不知道有什么无限级数,并且就我们所能得出的判断来讲,大多数系列都是有限的。一个六十岁的人死于癌症的机会是多少?显然我们可以计算这种结果,而无须假定在时间终结之前死于癌症的人数为无限大。但是照字面的解释来看,莱新巴哈的定义认为这是不可能的。
如果概率依靠按照时间顺序而不是按照其他可能的顺序来排列事件,那么概率就不能成为逻辑的一个分支,而必须是关于自然过程研究的一部分。这并不是莱新巴哈的看法;相反,他认为一切真正的逻辑都是概然逻辑,并且古典的逻辑的错误就在于把命题分为真伪两种,而不是把命题当作具有这种或那种程度概率的东西。所以他本来无须引入像时间这类现实世界中偶然性的特点,只用抽象的逻辑说法就能够叙述概率论中最基本的内容。
那种把概率当作统计的看法与莱新巴哈也在主张的那种认为一切命题由于缺少必然性而只具有不同程度的概然性的看法是很难结合在一起的。困难在于我们似乎陷入了无尽止的后退。假定我们说一个得瘟病的人死于这种病这句话带有概然性。这样说的意思是如果我们能够说出从最早的时代直到人类灭亡所有患瘟病的人所组成的系列,我们就将发现他们当中有半数以上死于这种病。因为将来和大部分过去都没有记载,我们就假定记载的情况是较好的样本。但是现在我们要记住我们的全部知识都只有概然性;所以如果我们在编写统计时发现记载上写着某甲得瘟病而死,我们一定不能把这个项目当作具有必然性而只能当作具有概然性的东西。为了发现它的概然性有多大,我们必须把它包括在一个系列中,比方说官方的死亡证明书中,而且我们必须找出某种方法确定死亡证明书有多大一部分是正确的。这里我们的统计中将有一个项目是:“布朗先生经过官方鉴定已经死亡,但是后来发现他仍然活着。”但是这句话又只能具有概然性,所以一定是记载的官方错误所组成的系列中的一个错误,这些错误之中有些后来发现并不是错误。这就是说我们必须收集人们错误地相信一个已被鉴定死亡的人后来却发现仍然活着的实例。这个过程永远也不会完结,如果我们的全部知识只具有概然性,并且概率又只是统计结果的话。如果我们想避免无尽止的后退,并且如果我们的全部知识只能具有概然性,那么我们就必须把“概然性”解释为“可信度”,并且必须通过统计以外的方法来计算。统计上的概率只能在真正的或假定的必然性的基础上来计算。
我将在谈到归纳时再来讲莱新巴哈。目前我想讲清楚我个人关于数学的概率与自然的进程之间的关联的看法。让我们就伯诺利的大数定律的一个实例进行具体说明,选择的是可能有的最简单情况。我们已经看到如果我们列出由n个不是1就是2的个位数组成的所有可能有的整数,那么如果n大的话——比方说不小于1000——可能出现的整数中有极大多数会具有相同数目的1和2。这只是下面这个事实的一个应用,即在(x+y)n的二项展开式中当n大时靠近中间的系数的和接近所有系数的和,这个和就是2n。但是这和如果我常常抛掷钱币我将得到出正面和出反面的数目大概会相等这个说法又有什么关系?一个是一件逻辑事实,而另一个则显然是一件经验的事实;它们之间的关联是什么?
就“概然性”的某些解释来说,一个包括“概然性”这个词在内的命题永远不能成为一个经验命题。人们承认不大可能的事可能发生,而可能的事却可能不发生。由此可以看出:实际发生的事并不说明先前一个概然性的判断是对还是错;每个可以想象的事件进程在逻辑上都可以和每个可以想象的事前的概然性估计不相冲突。否定这一点只能通过我们主张很少可能的事不会发生,而这一点正是我们没有权利来主张的。特别是如果归纳只断言概然性,那么不管发生的是什么事都可以和归纳的真和伪同时存在。所以归纳原理并没有经验的内容。这是一种归谬证法,表明我们必须把具有概然性的事情和实际发生的情况结合得比我们有时做的更为紧密。
如果我们坚持有限频率说——直到现在我还没有发现不这样做的理由——我们将说如果我们已知“a是一个B”而断言“a是一个A”具有概然性,那么我们的意思是说事实上B的大多数分子是A的分子。这是一个关于事实的命题,而不是一个关于a的命题。并且如果我说一个归纳论证(经过适当方式表达和限制之后)使其结论带有概然性,我的意思是说它是一类论证当中的一个,这类论证中大多数具有真的结论。
现在如果我说钱币出正面的机会是一半,那么这句话可能表示的意思是什么?首先,如果这句话为真,这就是一件经验的事实;从这件事实不能得出抛掷钱币只有出正面和出反面两种可能性的结论。如果能够这样,我们就能推论出一个生人叫作埃本尼兹·威尔克斯·史密斯的机会是一半,因为只有两种可能的选择,即他叫这个名字或者不叫这个名字。就某些钱币来说,出正面的次数多于出反面的次数;就另外一些钱币来说,出反面的次数多于出正面的次数。如果我不确指某个钱币而说出正面的机会是一半,那么我的话的意思是什么?
我的断言,同其他一切自认具有数学的精确性的关于经验的断言一样,一定只是近似性质的。我说一个人的身高是6英尺1英寸,我说这话时已经打出了误差范围;即使我发誓来说这句话,我也不会因为后来发现我的说法与实际相差百分之一英寸而犯伪誓的罪。同样,如果发现0.500001比我把钱币出正面的机会估计为0.5更为精确,我也不会被人认为是说了谎话。可是是否有任何证据能让我认为0.500001比0.5要好,这却值得怀疑。在概率问题上,像在其他问题上一样,我们也是采用接近符合事实的最简单的假设。比方说拿落体定律来讲。伽利略作了一定次数的观察,这些观察大体符合s=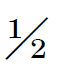 gt2这个公式。没有疑问他可能发现过一个函数f(t)使得s=f(t)更加精确地符合他的观察,但是他却宁愿要一个简单的足以符合观察的公式[7]。同样,如果我抛掷钱币2000次,出正面的次数是999次,而出反面的次数是1001,我就可以把出正面的机会看成一半。但是我用这句话所表示的精确意思到底是什么?
gt2这个公式。没有疑问他可能发现过一个函数f(t)使得s=f(t)更加精确地符合他的观察,但是他却宁愿要一个简单的足以符合观察的公式[7]。同样,如果我抛掷钱币2000次,出正面的次数是999次,而出反面的次数是1001,我就可以把出正面的机会看成一半。但是我用这句话所表示的精确意思到底是什么?
这个问题显示出莱新巴哈定义的力量。按照他的说法,我所表示的意思是:如果我相当长久地继续做下去,出正面的比例迟早将达到总在接近1/2左右;事实上,它与1/2之差将小于任何不管怎样小的分数。这是一个预言;如果预言正确,我的概率估计就正确,如果预言不正确,我的概率估计也不正确。有限频率说能够用什么理由来反对这一点呢?
我们必须把概率是多少与概率可能是多少区别开来。关于概率是多少的问题,这要决定于我们正在研究的抛掷的类。如果我们是在研究抛掷一个特指的钱币,那么如果在钱币的整个存在期间,这个钱币在全部n次抛掷当中将出m次正面,则该钱币出正面的概率就是m/n。如果我们是在研究一般的钱币,那么n就将是在世界历史的全部过去和将来中抛掷钱币的总数,而m就将是抛掷钱币将出正面的数目。为了不让问题的范围铺得太大,我们可以只研究本年内英格兰抛掷钱币的数目,或者只研究从事概率研究的人所列出的抛掷钱币的数目。在所有这些实例中,m和n是有限数,而m/n是在这些已知条件下出正面的概率。
但是上面所说的概率没有一种是已知的。我们因此必须对它们作出估计,这就是说,找出某种确定它们大概是多少的方法。如果我们要坚持有限频率说,这将表示我们的出正面和出反面的系列一定是某些有限类的系列之一,并且我们必须具有关于整个这一类的有用知识。我们将假定人们已经观察到在由某个特指的钱币的10,000次或更多次抛掷所组成的每一个系列中,在第5000次抛掷以后出正面的比例相差不会超过2ε,这里ε是很小的数。然后我们就可以说:就每个观察到的实例来说,某个特指的钱币在第5000次抛掷以后出正面的比例总在p-ε和p+ε之间,这里p是决定于钱币的一个常数。从这个实例推论到一个尚未观察到的实例是归纳的问题。如果使这个推论正确,我们将需要一个公理,即(在某些外界条件下)在所有观察到的实例中出现的一个特点在所有实例的很大一部分中也将出现;或者我们至少需要某个可以导出这种结论的公理。然后我们就能够从观察到的频率推论出可能出现的概率,按照有限频率说来解释概率。
上面所说的只是一种理论的大意。根据我所主张的理论,我想强调的要点是:每个概率叙述(与仅属可疑的陈述相对而言)都是关于一个系列中某一部分的事实叙述。特别是不管归纳原则是真还是伪,它都要断言作为一件事实来看,某些种类的大多数系列从始至终都具有一种特点,在这个系列的大量连续的项目中都有这种特点出现。如果这是事实,归纳论证就可能产生概率;如果不是事实,归纳论证就不能产生概率。我现在不是探讨我们怎样知道它是否是一件事实;这是我要留到我们所从事的研究的最后部分来谈的一个问题。
在上面的讨论中,我们将看到我们已经在许多论点上与莱新巴哈取得一致的意见,同时却一直不同意他给概率所下的定义。我对于他的定义所抱的主要反对意见是这个定义所依靠的频率是假言性质的和永远不能确定的。我同他的分歧还在于我比他更明确地把概然性和可疑性区别开来,以及我认为与必然逻辑相对的概然逻辑从逻辑上讲并不是最基本的东西。
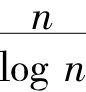 ,所以一个小于n的整数为质数的机会近似于
,所以一个小于n的整数为质数的机会近似于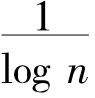 ,而在n无限增大时
,而在n无限增大时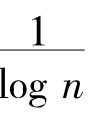 的极限为零。但是现在假定我们按照下面的方式重新排列整数:先排好前9个质数,然后排上第一个不是质数的数,再排好下9个质数,然后排上第二个不是质数的数,这样一直无限地排下去。当整数按照这种顺序排好之后,莱新巴哈的定义表明任意选取的一个数目为质数的机会是9/10。我们甚至能把整数安排得使一个数目不为质数的机会为零。为了得到这个结果,先排第一个非质数——即4——然后再在第n个非质数的后面排上已经排好的质数以后的n个质数;这个级数的开始是:4,1,6,2,3,8,5,7,11,9,13,17,19,23,10,29,31,37,41,43,12,……。在这个排列中,在第(n+1)个非质数之前将有n个非质数和
的极限为零。但是现在假定我们按照下面的方式重新排列整数:先排好前9个质数,然后排上第一个不是质数的数,再排好下9个质数,然后排上第二个不是质数的数,这样一直无限地排下去。当整数按照这种顺序排好之后,莱新巴哈的定义表明任意选取的一个数目为质数的机会是9/10。我们甚至能把整数安排得使一个数目不为质数的机会为零。为了得到这个结果,先排第一个非质数——即4——然后再在第n个非质数的后面排上已经排好的质数以后的n个质数;这个级数的开始是:4,1,6,2,3,8,5,7,11,9,13,17,19,23,10,29,31,37,41,43,12,……。在这个排列中,在第(n+1)个非质数之前将有n个非质数和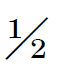 n(n+1)个质数;这样随着n的增大,非质数的数目与质数的数目之比就趋近于0,而以0为极限。
n(n+1)个质数;这样随着n的增大,非质数的数目与质数的数目之比就趋近于0,而以0为极限。