-
1.1推荐序 解放思想
-
1.2引言 洞悉人类思维的奥秘
-
1.301史上著名的思想实验
-
1.3.1思想实验1:地质的隐喻
-
1.3.2思想实验2:驾乘光束
-
1.3.3大脑新皮质的统一模式
-
1.402思考的思想实验
-
1.4.1思考,人脑不同于计算机
-
1.4.2字母表的倒背难题,记忆是连贯有序的
-
1.4.3联想因触发而生
-
1.4.4从刷牙到写诗,不可或缺的记忆层级
-
1.503大脑新皮质模型,思维模式识别理论
-
1.5.1模式的层级
-
1.5.2模式的结构
-
1.5.3流向大脑新皮质模式识别器的数据本质
-
1.5.4自联想和恒常性
-
1.5.5学习
-
1.5.6思想的语言
-
1.5.7梦的语言
-
1.5.8模型的根源
-
1.604人类的大脑新皮质
-
1.6.1智能,一个重要的进化分支
-
1.6.2新皮质的分层学习能力
-
1.6.3积木式神经元集合,思维模式识别的基础
-
1.6.4视觉皮质与通用算法
-
1.705旧脑
-
1.7.1感觉通路
-
1.7.2丘脑
-
1.7.3海马体
-
1.7.4小脑
-
1.7.5控制快乐与恐惧权
-
1.806新皮质的卓越能力
-
1.8.1天分
-
1.8.2创造力
-
1.8.3爱情
-
1.907仿生数码新皮质
-
1.9.1脑模拟
-
1.9.2神经网络
-
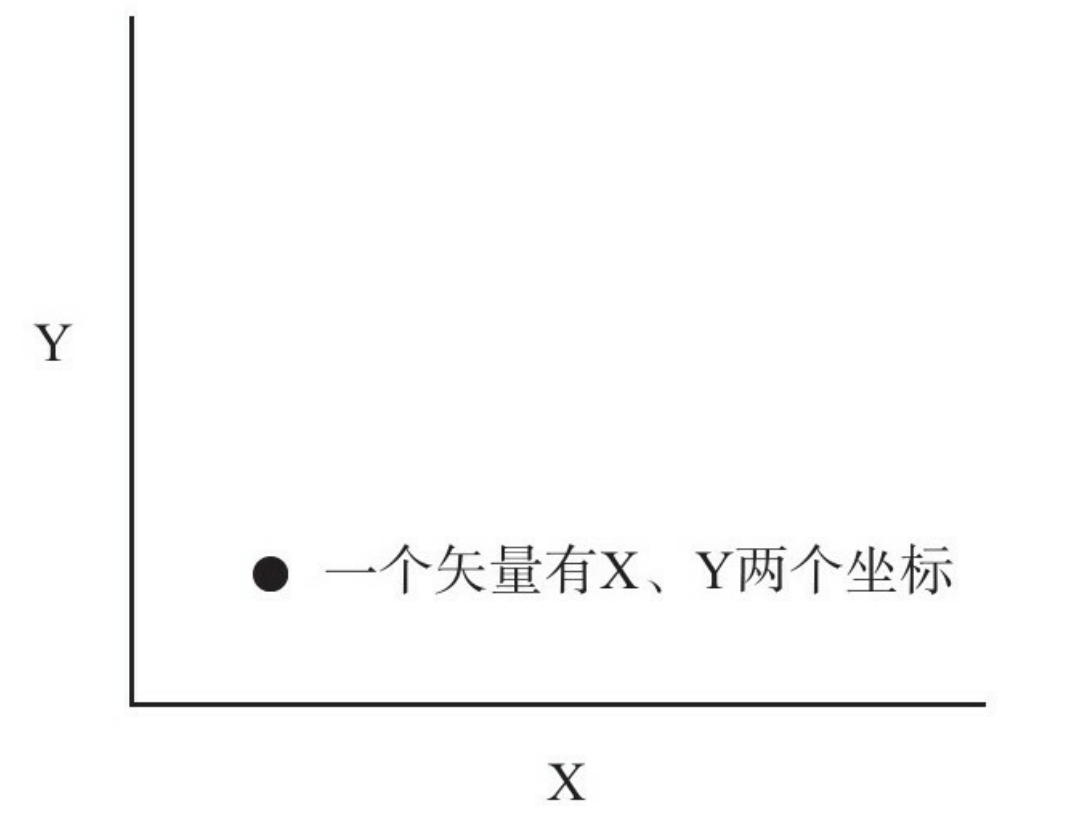
1.9.3矢量量化
-
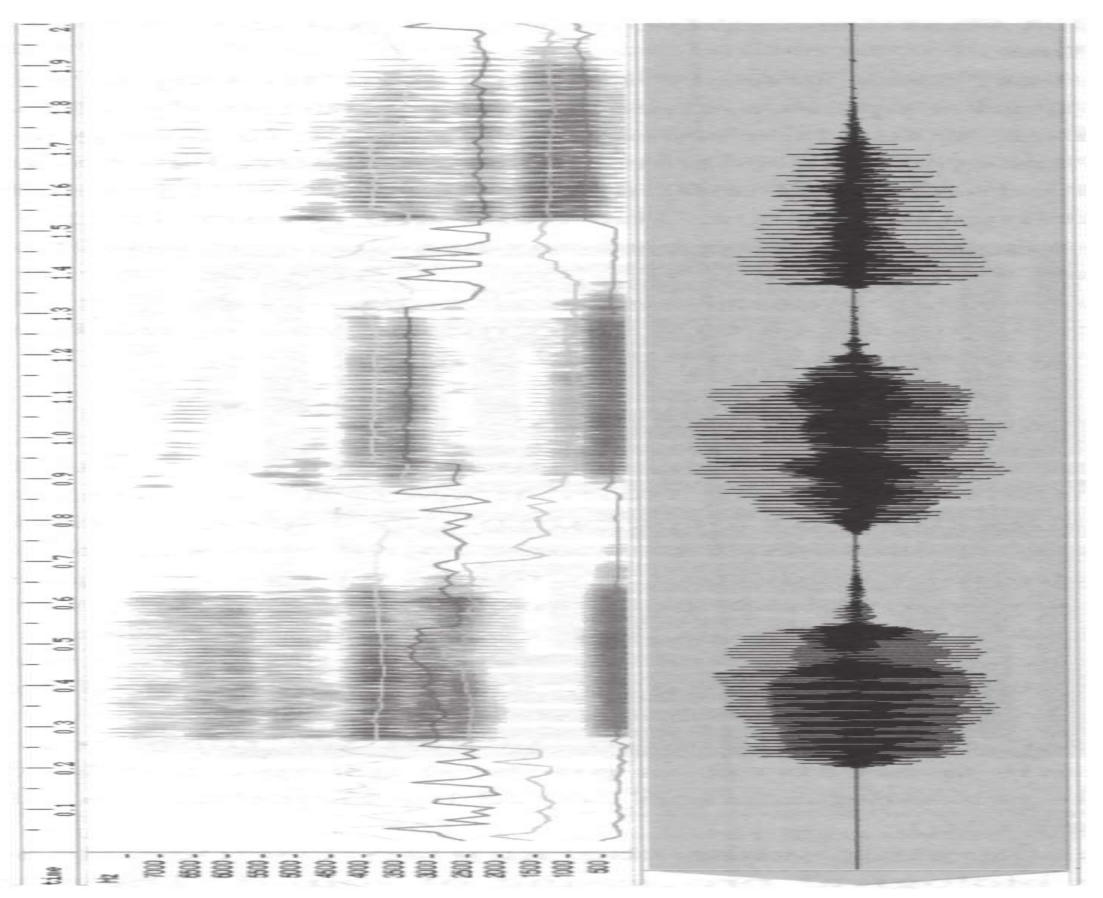
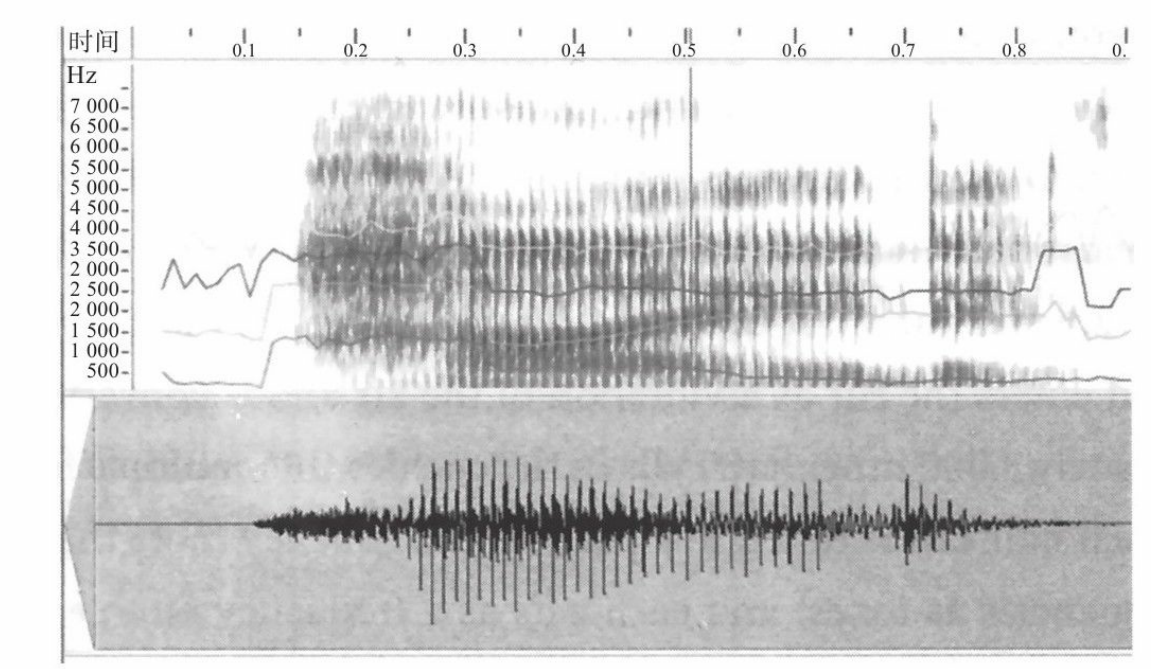
1.9.4用隐马尔可夫模型解读你的思维
-
1.9.5进化(遗传)算法
-
1.9.6列表处理语言LISP
-
1.9.7分层记忆系统
-
1.9.8人工智能前沿:登上能力层级顶端
-
1.9.9创建人工大脑
-
1.1008模拟人脑,计算机不可或缺的4大思维
-
1.10.1准确的沟通、记忆和计算能力
-
1.10.2计算的通用性
-
1.10.3冯·诺依曼结构
-
1.10.4按大脑核心算法进行创造性思考
-
1.1109思维的思想实验
-
1.11.1谁是有意识的
-
1.11.2你必须有信仰
-
1.11.3我们能够意识到什么
-
1.11.4东方是东方,西方是西方
-
1.11.5自由意志
-
1.11.6本体意识
-
1.1210有关思维的加速回报定律
-
1.12.1生物医学
-
1.12.2信息传输
-
1.12.3大脑研究与再造
-
1.1311反对大浪潮
-
1.13.1“奇点遥远”论
-
1.13.2“量子计算能力缺失”论
-
1.13.3“无意识”论
-
1.14后记 拥抱“奇点”
-
1.15注释
-
1.16译者后记
1
人工智能的未来