-
1.1前 言
-
1.2第一章 数学课学法指要
-
1.2.1第一节 明确学习高中数学的意义
-
1.2.2第二节 了解特点与重点
-
1.2.3第三节 数学基础知识的学习方法
-
1.2.4第四节 重视学思想方法和语言的学习
-
1.2.5第五节 学会解答与探索数学题
-
1.3第二章 综合学习指导
-
1.3.1第一节 研究性学习
-
1.3.2第二节 课题学习法
-
1.3.3第三节 问题学习法
-
1.3.4第四节 小组讨论学习法
-
1.3.5第五节 发现定法
-
1.3.6第六节 自主学习法
-
1.3.7第七节 活动学习法
-
1.3.8第八节 案例学习法
-
1.3.9第九节 基于数学开放题的学习法
-
1.3.10第十节 师生讨论学习法
-
1.3.11第十一节 探究性学习
-
1.3.12第十二节 合作互动学习
-
1.3.13第十三节 开放学习法
-
1.4第三章 数学思想方法
-
1.4.1第一节 符号化思想
-
1.4.2第二节 函数和方程思想
-
1.4.3第三节 公理化方法
-
1.4.4第四节 演绎推理思想
-
1.4.5第五节 模糊数学的数学思维方法
-
1.4.6第六节 反例思想
-
1.4.7第七节 集合思想
-
1.5第四章 解题方法指导
-
1.5.1第一节 化归法
-
1.5.2第二节 观察与实验
-
1.5.3第三节 数学模型方法
-
1.5.4第四节 分类讨论法
-
1.5.5第五节 数学抽象方法
-
1.6第五章 教学方法指导
-
1.6.1第一节 目标教学法
-
1.6.2第二节 再创造教学模式
-
1.6.3第三节 发现教学法
-
1.6.4第四节 单元教学法
-
1.6.5第五节 讲解式教学法
-
1.6.6第六节 读书指导教学法
-
1.6.7第七节 活动型教学法
-
1.6.8第八节 问题解决教学法
-
1.6.9第九节 师生谈话法
-
1.6.10第十节 小组讨论教学法
-
1.6.11第十一节 变式教学法
-
1.6.12第十二节 程序教学法
-
1.6.13第十三节 主体性教学法
-
1.6.14第十四节 合作性教学法
-
1.6.15第十五节 分层次教学法
-
1.6.16第十六节 探究式教学法
-
1.6.17第十七节 “问题-探究-问题”教学法
-
1.6.18第十八节 数学建模教学法
1
巧用数学方法
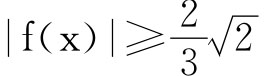
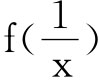 ,x和
,x和 互为倒数,把x换以
互为倒数,把x换以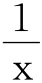 ,就可得到隐含于式①中的另一个条件:
,就可得到隐含于式①中的另一个条件: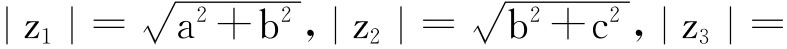
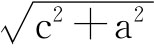 ,再利用复数不等式去证,问题就变得非常容易。
,再利用复数不等式去证,问题就变得非常容易。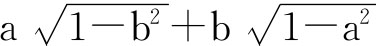 的值。
的值。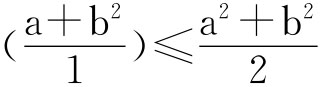 。实质上是一个应用很广的公式,很多有关不等式的证明可以归结于它。
。实质上是一个应用很广的公式,很多有关不等式的证明可以归结于它。