-
1.1应用型本科信息大类专业“十二五”规划教材
-
1.2前 言
-
1.3第1章 绪 论
-
1.3.11.1 基本术语
-
1.3.21.2 数据结构的内容
-
1.3.31.3 算法描述
-
1.3.41.4 算法分析
-
1.3.5习 题 1
-
1.4第2章 线 性 表
-
1.4.12.1 线性表的定义及运算
-
1.4.22.2 线性表的顺序存储结构
-
1.4.32.3 线性表的链式存储结构
-
1.4.42.4 循环链表
-
1.4.52.5 双向链表
-
1.4.62.6 多项式相加
-
1.4.7习 题 2
-
1.5第3章 栈和队列
-
1.5.13.1 栈的定义及抽象数据类型
-
1.5.23.2 栈的实现
-
1.5.33.3 栈的应用举例
-
1.5.43.4 队列的定义及抽象数据类型
-
1.5.53.5 队列的实现
-
1.5.63.6 队列的应用举例
-
1.5.7习 题 3
-
1.6第4章 串
-
1.6.14.1 串定义
-
1.6.24.2 串的存储方法
-
1.6.34.3 串操作
-
1.6.4习 题 4
-
1.7第5章 矩阵与广义表
-
1.7.15.1 矩阵
-
1.7.25.2 特殊矩阵
-
1.7.35.3 稀疏矩阵的运算
-
1.7.45.4 广义表
-
1.7.55.5 广义表的运算
-
1.7.6习 题 5
-
1.8第6章 树
-
1.8.16.1 树的定义和术语
-
1.8.26.2 二叉树
-
1.8.36.3 遍历二叉树和线索二叉树
-
1.8.46.4 二叉树的转换
-
1.8.56.5 二叉树的应用
-
1.8.66.6 哈夫曼树及其应用
-
1.8.7习 题 6
-
1.9第7章 图
-
1.9.17.1 图的定义与基本术语
-
1.9.27.2 图的存储结构
-
1.9.37.3 图的遍历和生成树
-
1.9.47.4 最小生成树
-
1.9.57.5 最短路径
-
1.9.67.6 拓扑排序
-
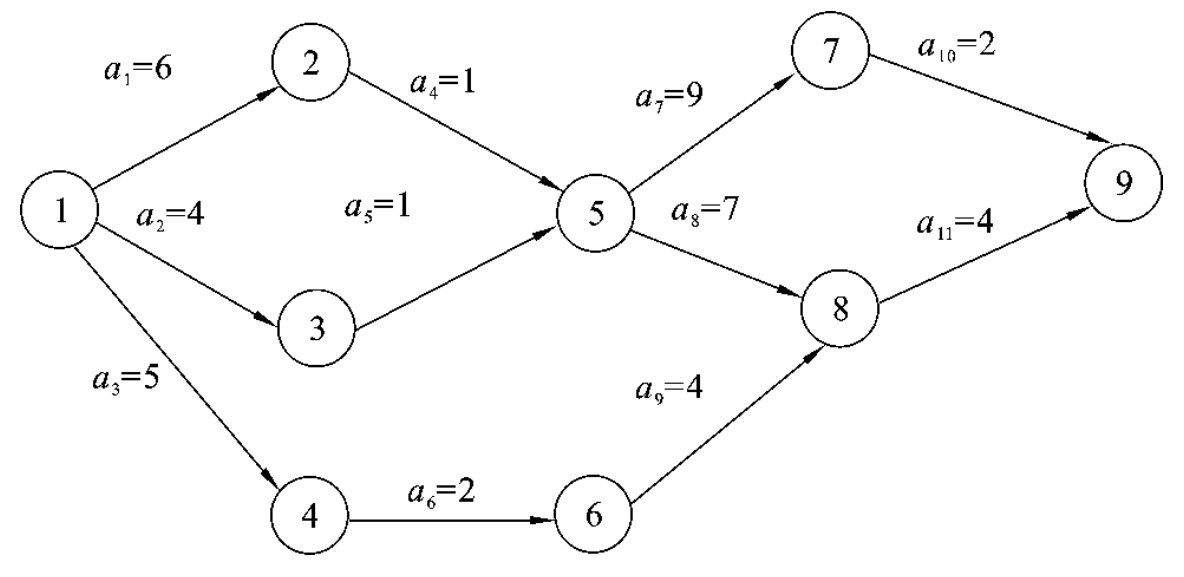
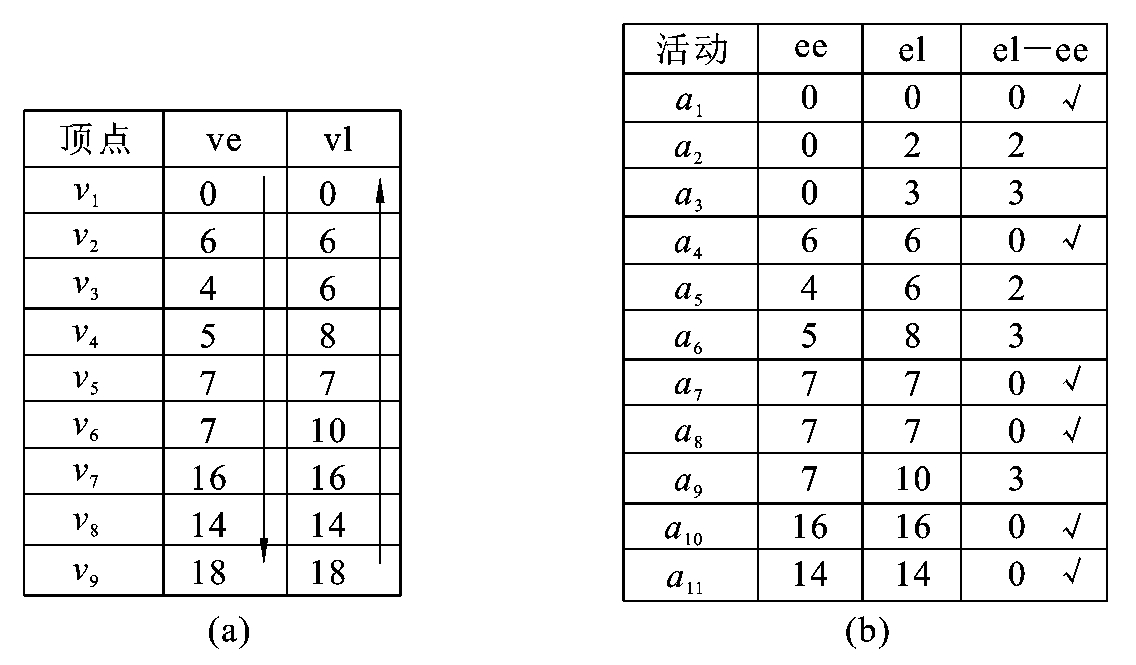
1.9.77.7 关键路径
-
1.9.8习 题 7
-
1.10第8章 查 找
-
1.10.18.1 顺序查找
-
1.10.28.2 折半查找
-
1.10.38.3 分块查找
-
1.10.48.4 树型查找
-
1.10.58.5 散列查找
-
1.10.6习 题 8
-
1.11第9章 内 排 序
-
1.11.19.1 排序的基本概念
-
1.11.29.2 直接插入排序
-
1.11.39.3 简单选择排序
-
1.11.49.4 起泡排序
-
1.11.59.5 堆排序
-
1.11.69.6 快速排序
-
1.11.79.7 归并排序
-
1.11.89.8 基数排序
-
1.11.99.9 7种排序方法的比较
-
1.11.10习 题 9
-
1.12第10章 文 件
-
1.12.110.1 概述
-
1.12.210.2 文件组织
-
1.12.310.3 动态索引
-
1.12.4习 题 10
-
1.13参考文献
1
数据结构