-
1.12009年度山东省社会科学普及读物出版资助重点项目文丛
-
1.2前 言
-
1.3生活离不开经济学
-
1.4第一篇 家庭和企业——开源节流节节高
-
1.4.11 如何选择看成本——选择与机会成本
-
1.4.22 当家方知柴米贵——消费选择与预算支出最佳原则
-
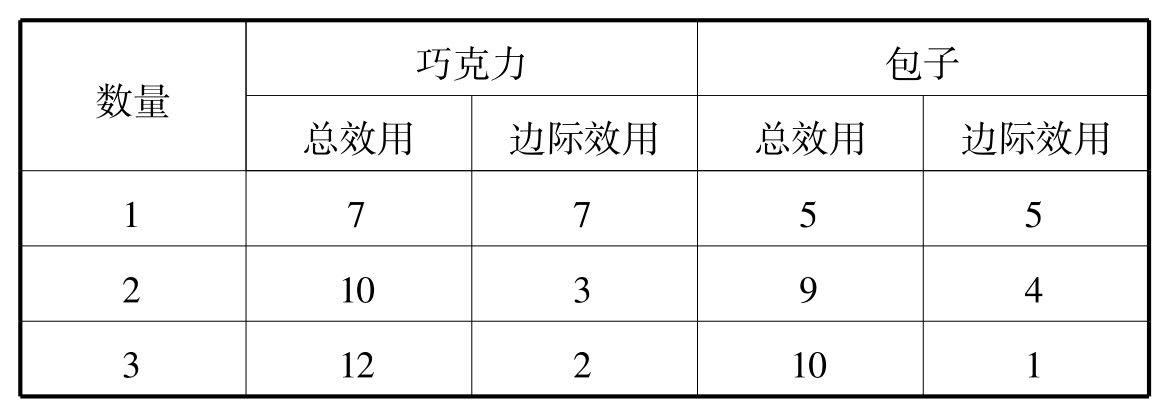
1.4.33 消费增加效用减——价格悖论与边际效用递减规律
-
1.4.44 政策作用有不同——收入变化与产品选择
-
1.4.55 有钱不怕没货买——替代品与竞争
-
1.4.66 就怕大头在后头——互补品与耗材支出
-
1.4.77 生意越大越好赚——规模经济与自然垄断
-
1.4.88 投入增加产量降——肥大水勤与边际报酬递减规律
-
1.4.99 明知亏损还生产——经营决策与停止营业点
-
1.5第二篇 市场结构——一切皆为利来往
-
1.5.110 身不由己话竞争——价格接受者与完全竞争市场
-
1.5.211 扎堆生产也获利——企业生存与零利润定理
-
1.5.312 酒香也怕巷子深——垄断竞争与品牌建设
-
1.5.413 策略不变是最优——三聚氰胺事件与占优策略均衡
-
1.5.514 你降我降大家亏——价格战与纳什均衡
-
1.5.615 天天斗来何时休——信用缺失与重复博弈
-
1.5.716 想吃独食受管制——寡头垄断与法律管制
-
1.5.817 购物自带方便袋——限塑令与外部性
-
1.5.918 价格降低好货无——旧车市场与逆向选择
-
1.5.1019 合同签后要防范——道德风险与委托—代理
-
1.5.1120 限制价格就停产——垄断与价格管制
-
1.5.1221 光占便宜不出力——免费搭便车与公共物品
-
1.6第三篇 民生问题——国家干预求发展
-
1.6.122 经济形势如何看——宏观经济运行与宏观经济政策目标
-
1.6.223 政府购买拉内需——三驾马车与总需求公式
-
1.6.324 降息减税促经济——扩大内需与财政货币“组合拳”
-
1.6.425 就业是个大问题——就业与国家宏观调控
-
1.6.526 柴米油盐系民生——消费价格指数与通货膨胀
-
1.6.627 总量增加非强大——经济实力与GDP
-
1.6.728 发展才是硬道理——经济增长与经济发展
-
1.6.829 税率提高税收减——个人所得税与拉弗曲线
-
1.7第四篇 对外交往——国内国外谋生存
-
1.7.130 全球都由我生产——中国制造与相对比较优势
-
1.7.231 货币升值好是坏——人民币升值与汇率
-
1.7.332 贸易顺差惹争议——出口与贸易摩擦
-
1.7.433 出口商品遭控告——出口与反倾销
-
1.7.534 他国商品进入难——出口与贸易壁垒
-
1.7.6后 记
1
生活中的经济学