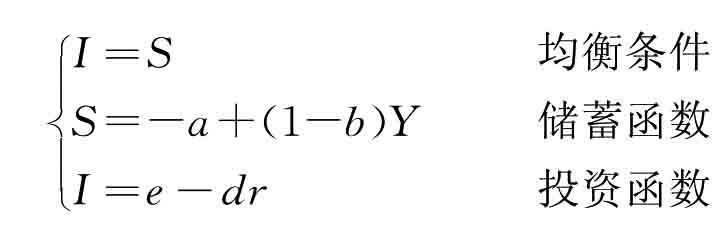-
1.1前 言
-
1.2第一章 导 论
-
1.2.1学习目标
-
1.2.2第一节 宏观经济学的涵义
-
1.2.2.1一、宏观经济学的研究对象
-
1.2.2.2二、宏观经济学的理论体系
-
1.2.3第二节 宏观经济学的一些基本概念
-
1.2.3.1一、国内生产总值
-
1.2.3.2二、通货膨胀和通货紧缩
-
1.2.3.3三、失业和失业率
-
1.2.4第三节 学习和研究宏观经济学的意义
-
1.2.4.1一、从微观到宏观
-
1.2.4.2二、宏观经济学与个人职业生涯发展和企业经营管理
-
1.3第二章 国民收入核算
-
1.3.1学习目标
-
1.3.2第一节 国内生产总值
-
1.3.2.1一、国内生产总值的定义
-
1.3.2.2二、名义GDP和实际GDP
-
1.3.2.3三、最终产品和中间产品
-
1.3.2.4四、存量和流量
-
1.3.2.5五、当前生产和销售
-
1.3.2.6六、国内生产总值和国民生产总值
-
1.3.2.7七、市场活动与非市场活动
-
1.3.2.8八、国内生产总值指标存在的若干问题
-
1.3.3第二节 国内生产总值核算的基本方法
-
1.3.3.1一、总产出、总收入与总支出
-
1.3.3.2二、收入法
-
1.3.3.3三、支出法
-
1.3.4第三节 国民经济中的其他主要经济总量指标
-
1.3.4.1一、国民生产总值
-
1.3.4.2二、国内生产净值
-
1.3.4.3三、国民生产净值
-
1.3.4.4四、国民收入
-
1.3.4.5五、个人收入
-
1.3.4.6六、个人可支配收入
-
1.3.5第四节 国民收入核算中的恒等关系
-
1.3.5.1一、两部门经济中的储蓄投资恒等式
-
1.3.5.2二、三部门经济中的储蓄投资恒等式
-
1.3.5.3三、四部门经济中的储蓄投资恒等式
-
1.4第三章 消费和储蓄理论
-
1.4.1学习目标
-
1.4.2第一节 消费和消费函数
-
1.4.2.1一、消费支出及其影响因素
-
1.4.2.2二、消费函数
-
1.4.2.3三、国民消费函数
-
1.4.3第二节 储蓄和储蓄函数
-
1.4.3.1一、储蓄函数
-
1.4.3.2二、消费函数和储蓄函数的关系
-
1.4.4第三节 现代消费理论及其发展
-
1.4.4.1一、相对收入假说
-
1.4.4.2二、持久收入假说
-
1.4.4.3三、生命周期假说
-
1.5第四章 投资理论
-
1.5.1学习目标
-
1.5.2第一节 概 述
-
1.5.2.1一、宏观经济学中的投资概念
-
1.5.2.2二、决定投资的主要因素
-
1.5.3第二节 资本边际效率与投资的决定
-
1.5.3.1一、资本的未来收益贴现率与资产的现值
-
1.5.3.2二、资本边际效率
-
1.5.3.3三、投资函数
-
1.5.4第三节 投资的加速原理
-
1.5.4.1一、资本—产出比率
-
1.5.4.2二、加速原理
-
1.5.5第四节 固定资产投资和存货投资
-
1.5.5.1一、固定资产投资的新古典模型
-
1.5.5.2二、存货投资
-
1.6第五章 国民收入决定的收入支出模型
-
1.6.1学习目标
-
1.6.2第一节 总需求与均衡产出和均衡收入
-
1.6.2.1一、国民经济中的总需求
-
1.6.2.2二、国民经济的均衡条件
-
1.6.3第二节 两部门经济的收入支出模型
-
1.6.3.1一、消费函数与均衡国民收入
-
1.6.3.2二、投资、储蓄和均衡国民收入
-
1.6.3.3三、两部门经济中均衡的比较静态分析
-
1.6.4第三节 乘数理论
-
1.6.4.1一、国民收入决定的动态分析
-
1.6.4.2二、乘数的含义
-
1.6.4.3三、乘数的数学推导和图解
-
1.6.5第四节 三部门和四部门经济的收入支出模型
-
1.6.5.1一、引入政府部门
-
1.6.5.2二、三部门经济的收入支出模型
-
1.6.5.3三、三部门经济中的乘数
-
1.6.5.4四、四部门经济的收入支出模型
-
1.7第六章 货币需求和货币供给
-
1.7.1学习目标
-
1.7.2第一节 货币的性质和发展
-
1.7.2.1一、货币的性质
-
1.7.2.2二、货币的发展
-
1.7.2.3三、现代货币层次
-
1.7.3第二节 银行体系与货币创造
-
1.7.3.1一、银行体系
-
1.7.3.2二、存款创造与货币供给
-
1.7.4第三节 货币需求
-
1.7.4.1一、货币需求和货币需求动机
-
1.7.4.2二、影响货币需求的因素
-
1.7.4.3三、货币需求函数
-
1.7.5第四节 货币市场均衡
-
1.7.5.1一、均衡利率的决定
-
1.7.5.2二、均衡利率和均衡货币量的变动
-
1.8第七章 扩展的凯恩斯宏观经济模型:IS‐LM模型
-
1.8.1学习目标
-
1.8.2第一节 产品市场均衡
-
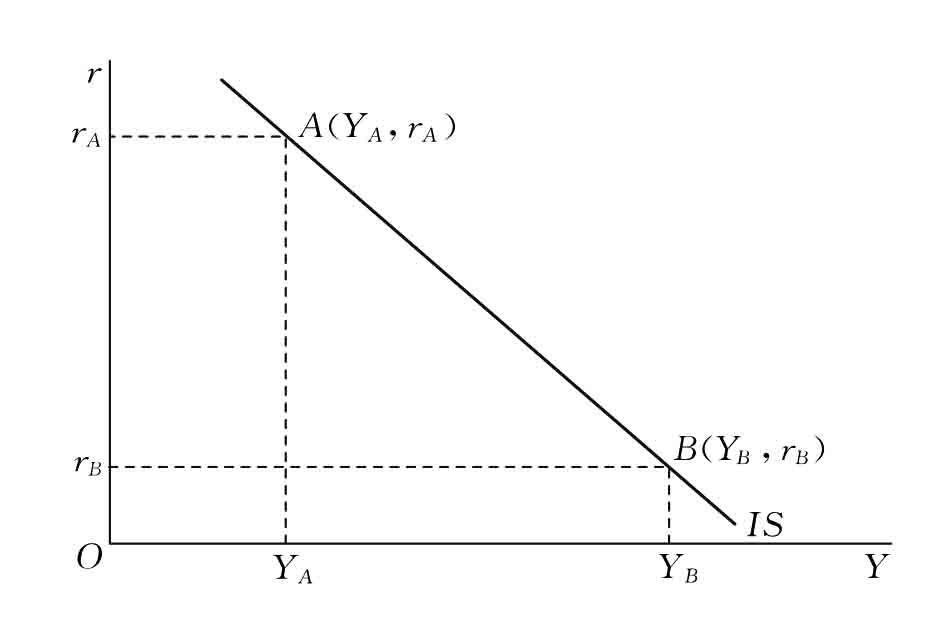
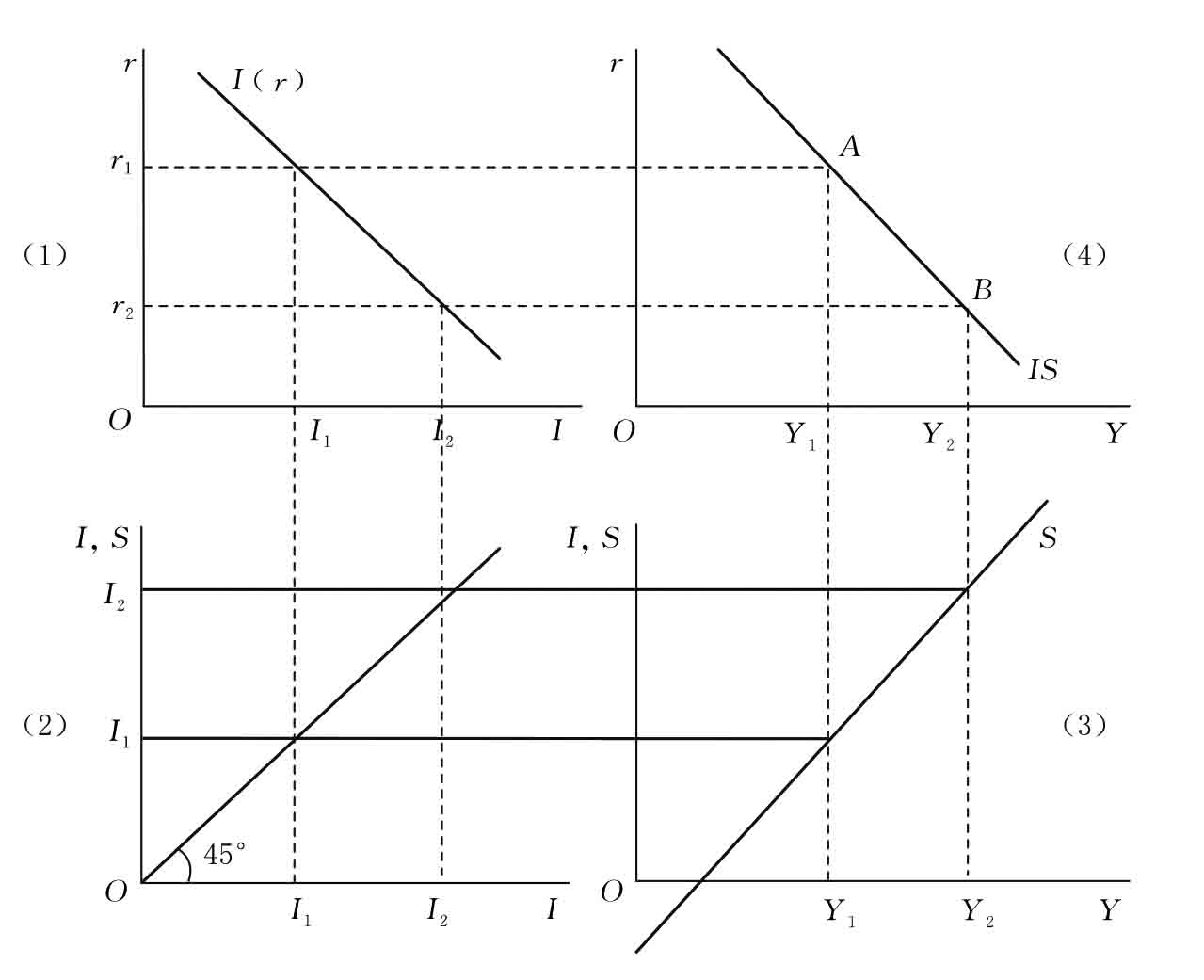
1.8.2.1一、产品市场均衡曲线的推导
-
1.8.2.2二、犐犛曲线的特征
-
1.8.2.3三、产品市场的失衡
-
1.8.3第二节 货币市场的均衡
-
1.8.3.1一、货币市场均衡曲线的推导
-
1.8.3.2二、LM曲线的特征
-
1.8.3.3三、货币市场的失衡
-
1.8.4第三节 产品市场与货币市场的一般均衡
-
1.8.4.1一、均衡利率和均衡收入的决定
-
1.8.4.2二、市场均衡的比较静态分析
-
1.8.4.3三、IS‐LM模型的政策含义
-
1.9第八章 国民收入决定的AD‐AS模型
-
1.9.1学习目标
-
1.9.2第一节 总需求曲线
-
1.9.2.1一、总需求曲线的推导
-
1.9.2.2二、总需求曲线的特征
-
1.9.3第二节 总供给曲线
-
1.9.3.1一、劳动力市场均衡与总供给
-
1.9.3.2二、总供给曲线的推导
-
1.9.3.3三、凯恩斯主义总供给函数
-
1.9.3.4四、古典学派总供给函数
-
1.9.4第三节 总供求模型
-
1.9.4.1一、古典学派总供求模型
-
1.9.4.2二、凯恩斯主义总供求模型
-
1.9.4.3三、总供求模型的政策含义
-
1.10第九章 宏观经济的主要问题:通货膨胀和失业
-
1.10.1学习目标
-
1.10.2第一节 通货膨胀
-
1.10.2.1一、通货膨胀的定义与衡量
-
1.10.2.2二、通货膨胀的类型
-
1.10.2.3三、通货膨胀的成因
-
1.10.2.4四、通货膨胀的成本
-
1.10.2.5五、通货膨胀的经济效应
-
1.10.2.6六、通货膨胀的治理对策
-
1.10.3第二节 失业及其对国民经济的影响
-
1.10.3.1一、失业及其类型
-
1.10.3.2二、失业的成本和奥肯定律
-
1.10.3.3三、自然失业率及其决定因素
-
1.10.4第三节 通货膨胀和失业的替代关系
-
1.10.4.1一、菲利普斯曲线
-
1.10.4.2二、预期和菲利普斯曲线
-
1.10.4.3三、长期菲利普斯曲线
-
1.11第十章 宏观经济政策的原理和运用
-
1.11.1学习目标
-
1.11.2第一节 财政政策
-
1.11.2.1一、财政政策工具
-
1.11.2.2二、自动稳定器
-
1.11.2.3三、挤出效应
-
1.11.2.4四、财政政策的限制
-
1.11.3第二节 货币政策
-
1.11.3.1一、货币政策工具
-
1.11.3.2二、货币政策的传导机制
-
1.11.3.3三、货币政策效果
-
1.11.3.4四、货币政策的限制
-
1.12第十一章 经济周期波动
-
1.12.1学习目标
-
1.12.2第一节 经济周期概述
-
1.12.2.1一、经济周期的定义和阶段
-
1.12.2.2二、经济周期的类型
-
1.12.3第二节 经济周期的基本理论
-
1.12.3.1一、经济周期理论的分类
-
1.12.3.2二、单一因素周期理论
-
1.12.3.3三、实业周期理论
-
1.12.3.4四、储蓄投资过程周期理论
-
1.12.3.5五、新古典主义周期理论
-
1.12.4第三节 卡尔多经济周期模型
-
1.12.4.1一、投资函数和储蓄函数的扩展分析
-
1.12.4.2二、投资和储蓄的多重均衡
-
1.12.4.3三、经济周期模型
-
1.12.5第四节 乘数-加速数相互作用模型
-
1.12.5.1一、模型框架
-
1.12.5.2二、国民收入的动态变化
-
1.13第十二章 宏观经济的长期增长
-
1.13.1学习目标
-
1.13.2第一节 经济增长概述
-
1.13.2.1一、经济增长和经济发展的含义
-
1.13.2.2二、经济增长的主要因素
-
1.13.3第二节 哈罗德-多马经济增长模型
-
1.13.3.1一、模型框架
-
1.13.3.2二、经济增长的动态路径
-
1.13.4第三节 新古典增长模型
-
1.13.4.1一、集约形态的总量生产函数
-
1.13.4.2二、新古典增长模型的基本框架
-
1.13.4.3三、储蓄率变动的影响
-
1.13.4.4四、劳动力增长率变动的影响
-
1.13.4.5五、资本的黄金律水平
-
1.13.4.6六、技术进步对经济增长的影响
-
1.14参考文献
1
宏观经济学
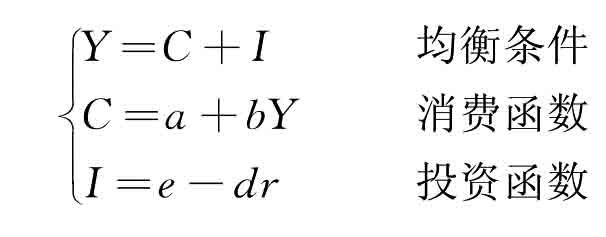
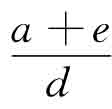 、斜率为
、斜率为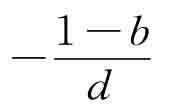 的直线,由于这一表达式是在产品市场均衡条件基础上推导出来的,因此,该直线上任何一点代表的利率和收入组合均能使产品市场达到均衡。
的直线,由于这一表达式是在产品市场均衡条件基础上推导出来的,因此,该直线上任何一点代表的利率和收入组合均能使产品市场达到均衡。