新编大学计算机基础
-
1.1《新编大学计算机基础》编 委 会
-
1.2前 言
-
1.3第一章 电子计算机基础知识
-
1.3.11.1 电子计算机的概念和特点
-
1.3.21.2 电子计算机的产生与发展
-
1.3.31.3 电子计算机的分类及应用
-
1.3.3.11.3.1 电子计算机的分类
-
1.3.3.21.3.2 电子计算机的应用
-
1.3.41.4 数制基础
-
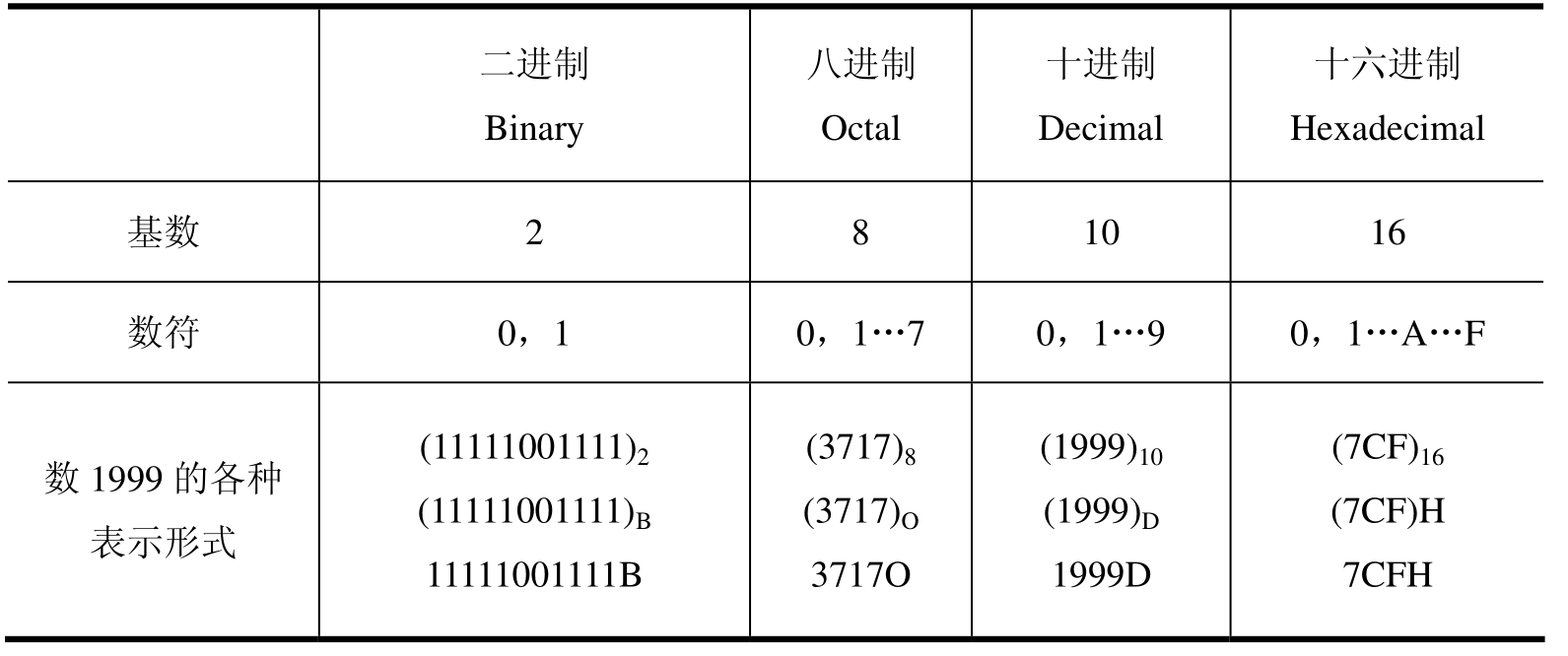
1.3.4.11.4.1 数制的概念
-
1.3.4.21.4.2 各种数制的转化
-
1.3.4.31.4.3 二进制的运算规则
-
1.3.51.5 计算机中数据与信息的表示方法
-
1.3.5.11.5.1 数据与信息的概念
-
1.3.5.21.5.2 计算机中数的表示方法
-
1.3.5.31.5.3 计算机中的信息编码
-
1.4第二章 微机系统基本组成
-
1.4.12.1 微机的硬件系统
-
1.4.1.12.1.1 电子数字计算机的基本组成
-
1.4.1.22.1.2 中央处理器
-
1.4.1.32.1.3 存储器
-
1.4.1.42.1.4 输入/输出设备
-
1.4.1.52.1.5 微机主板、总线和接口
-
1.4.22.2 微机的软件系统
-
1.4.2.12.2.1 系统软件
-
1.4.2.22.2.2 应用软件
-
1.4.2.32.2.3 软件的知识产权保护
-
1.4.32.3 微机的配置与主要性能指标
-
1.4.3.12.3.1 微机的配置
-
1.4.3.22.3.2 微机主要性能指标
-
1.4.42.4 微机安全知识
-
1.4.4.12.4.1 微机常见故障
-
1.4.4.22.4.2 计算机病毒简介
-
1.4.4.32.4.3 计算机安全操作
-
1.5第三章 操作系统
-
1.5.13.1 操作系统概述
-
1.5.23.2 几种常用的操作系统
-
1.5.33.3 Windows XP基本操作
-
1.5.3.13.3.1 Windows XP的启动、退出、用户管理
-
1.5.3.23.3.2 Windows XP桌面
-
1.5.3.33.3.3 鼠标的基本操作
-
1.5.3.43.3.4 窗口
-
1.5.3.53.3.5 菜单
-
1.5.3.63.3.6 对话框
-
1.5.43.4 应用程序
-
1.5.4.13.4.1 启动应用程序
-
1.5.4.23.4.2 退出应用程序
-
1.5.53.5 Windows XP的文件管理功能
-
1.5.5.13.5.1 “我的电脑”的使用
-
1.5.5.23.5.2 资源管理器的使用
-
1.5.5.33.5.3 文件及文件夹的基本操作
-
1.5.5.43.5.4 建立快捷方式
-
1.5.5.53.5.5 剪贴板及回收站的使用
-
1.5.63.6 磁盘管理
-
1.5.6.13.6.1 格式化磁盘
-
1.5.6.23.6.2 查看磁盘信息
-
1.5.73.7 控制面板的使用
-
1.5.7.13.7.1 启动控制面板
-
1.5.7.23.7.2 设置系统日期和时间
-
1.5.7.33.7.3 设置鼠标、键盘和输入法
-
1.5.7.43.7.4 用户管理
-
1.5.7.53.7.5 添加打印机
-
1.5.7.63.7.6 设置显示器属性
-
1.5.7.73.7.7 网上邻居的使用
-
1.5.7.83.7.8 安全中心
-
1.5.83.8 DOS操作系统简介及其常用命令
-
1.5.8.13.8.1 DOS操作系统简介
-
1.5.8.23.8.2 路径
-
1.5.8.33.8.3 DOS常用命令
-
1.6第四章 文字处理软件Word 2000
-
1.6.14.1 Word 2000概述
-
1.6.1.14.1.1 Word 2000的主要功能
-
1.6.1.24.1.2 Word的安装
-
1.6.1.34.1.3 Word的启动与退出
-
1.6.1.44.1.4 Word 2000窗口组成
-
1.6.1.54.1.5 Word 2000工具栏
-
1.6.24.2 Word文档的基本操作
-
1.6.2.14.2.1 创建Word文档
-
1.6.2.24.2.2 打开Word文档
-
1.6.2.34.2.3 关闭文档
-
1.6.2.44.2.4 保存文档
-
1.6.2.54.2.5 文档输入
-
1.6.2.64.2.6 光标移动
-
1.6.2.74.2.7 选定文本
-
1.6.2.84.2.8 编辑文档
-
1.6.2.94.2.9 查找与替换
-
1.6.2.104.2.10 拼写和语法检查
-
1.6.2.114.2.11 多窗口编辑
-
1.6.2.124.2.12 文档的保护
-
1.6.34.3 文档的排版
-
1.6.3.14.3.1 视图设置
-
1.6.3.24.3.2 字符格式设置
-
1.6.3.34.3.3 段落格式设置
-
1.6.3.44.3.4 分栏
-
1.6.44.4 表格制作
-
1.6.4.14.4.1 创建表格
-
1.6.4.24.4.2 表格编辑
-
1.6.4.34.4.3 表格的修饰
-
1.6.54.5 插入图形和艺术字
-
1.6.5.14.5.1 插入图形
-
1.6.5.24.5.2 编辑图片
-
1.6.5.34.5.3 绘制图形
-
1.6.5.44.5.4 插入和编辑艺术字
-
1.6.5.54.5.5 插入文本框
-
1.6.64.6 公式的制作
-
1.6.74.7 页面排版和打印文档
-
1.6.7.14.7.1 页面设置
-
1.6.7.24.7.2 页码和分隔符
-
1.6.7.34.7.3 页眉和页脚
-
1.6.7.44.7.4 插入脚注和尾注
-
1.6.7.54.7.5 预览与打印
-
1.6.84.8 样式及模板的使用
-
1.6.8.14.8.1 样式
-
1.6.8.24.8.2 模板
-
1.7第五章 电子表格Excel 2000
-
1.7.15.1 Excel 2000基本知识
-
1.7.1.15.1.1 Excel 2000的启动和退出
-
1.7.1.25.1.2 窗口基本元素和操作
-
1.7.1.35.1.3 Excel 2000工具栏
-
1.7.25.2 管理工作簿和工作表
-
1.7.2.15.2.1 基本概念
-
1.7.2.25.2.2 获得帮助
-
1.7.2.35.2.3 工作簿管理
-
1.7.35.3 工作表的编辑与格式化
-
1.7.3.15.3.1 单元格选择
-
1.7.3.25.3.2 输入数据
-
1.7.3.35.3.3 工作表编辑
-
1.7.3.45.3.4 工作表的格式化
-
1.7.45.4 公式与函数
-
1.7.4.15.4.1 自动计算
-
1.7.4.25.4.2 公式
-
1.7.55.5 数据管理
-
1.7.5.15.5.1 创建数据清单
-
1.7.5.25.5.2 数据排序
-
1.7.5.35.5.3 数据筛选
-
1.7.5.45.5.4 数据分类汇总
-
1.7.5.55.5.5 记录单
-
1.7.5.65.5.6 数据透视表
-
1.7.65.6 图 表
-
1.7.6.15.6.1 创建图表
-
1.7.6.25.6.2 图表格式化
-
1.7.6.35.6.3 图表工具栏
-
1.7.75.7 工作表打印
-
1.7.7.15.7.1 页面设置
-
1.7.7.25.7.2 分页控制
-
1.7.7.35.7.3 打印预览
-
1.7.7.45.7.4 打印工作表
-
1.7.85.8 工作表的其他操作
-
1.7.95.9 Excel与Word 2000的综合应用
-
1.7.9.15.9.1 插入Excel工作表对象
-
1.7.9.25.9.2 插入Excel工作表
-
1.7.9.35.9.3 链接Excel数据
-
1.8第六章 演示文稿制作软件PowerPoint
-
1.8.16.1 PowerPoint的基本操作
-
1.8.1.16.1.1 PowerPoint 2000的启动和退出
-
1.8.1.26.1.2 PowerPoint 2000的工作界面
-
1.8.1.36.1.3 菜单栏
-
1.8.1.46.1.4 工具栏
-
1.8.1.56.1.5 视图方式
-
1.8.26.2 演示文稿的创建和保存
-
1.8.2.16.2.1 使用“内容提示向导”创建演示文稿
-
1.8.2.26.2.2 从演示文稿出发创建演示文稿
-
1.8.2.36.2.3 从演示文稿的模板出发建立文稿
-
1.8.36.3 演示文稿的文件管理
-
1.8.3.16.3.1 打开演示文稿
-
1.8.3.26.3.2 演示文稿的保存
-
1.8.3.36.3.3 其他文件管理命令
-
1.8.46.4 PowerPoint窗口菜单
-
1.8.56.5 幻灯片的编辑
-
1.8.5.16.5.1 插入和删除幻灯片
-
1.8.5.26.5.2 移动和复制幻灯片
-
1.8.5.36.5.3 动画设计
-
1.8.5.46.5.4 超级链接的使用
-
1.8.66.6 演示文稿的放映
-
1.9第七章 多媒体应用基础
-
1.9.17.1 多媒体概述
-
1.9.1.17.1.1 文本(Text)
-
1.9.1.27.1.2 声音(Audio)
-
1.9.1.37.1.3 图形(Graph)
-
1.9.1.47.1.4 图像(Image)
-
1.9.1.57.1.5 动画(Animation)
-
1.9.1.67.1.6 视频(Video)
-
1.9.27.2 多媒体技术
-
1.9.2.17.2.1 多媒体技术的特征
-
1.9.2.27.2.2 多媒体关键技术
-
1.9.2.37.2.3 多媒体技术的应用
-
1.9.37.3 多媒体个人计算机
-
1.9.3.17.3.1 MPC硬件系统
-
1.9.3.27.3.2 MPC软件系统
-
1.9.47.4 常用工具简介
-
1.9.4.17.4.1 图像处理软件Photoshop
-
1.9.4.27.4.2 动画制作软件Flash
-
1.9.4.37.4.3 多媒体开发软件Authorware
-
1.9.4.47.4.4 图片浏览工具ACDSee
-
1.10第八章 计算机网络基础
-
1.10.18.1 计算机网络概述
-
1.10.1.18.1.1 计算机网络的定义
-
1.10.1.28.1.2 计算机网络的发展历史
-
1.10.1.38.1.3 计算机网络的分类
-
1.10.1.48.1.4 计算机网络的拓扑结构
-
1.10.1.58.1.5 计算机网络的主要功能
-
1.10.28.2 计算机通信
-
1.10.2.18.2.1 计算机通信的概念
-
1.10.2.28.2.2 模拟数据通信和数字数据通信
-
1.10.2.38.2.3 线路复用技术
-
1.10.2.48.2.4 数据交换技术
-
1.10.38.3 计算机网络的硬软件系统简介
-
1.10.3.18.3.1 网络硬件系统
-
1.10.3.28.3.2 网络软件系统
-
1.10.48.4 计算机网络的体系结构
-
1.10.4.18.4.1 ISO/OSI参考模型
-
1.10.4.28.4.2 TCP/IP参考模型与协议
-
1.10.58.5 Internet基础
-
1.10.5.18.5.1 什么是Internet
-
1.10.5.28.5.2 Internet的发展
-
1.10.5.38.5.3 Internet提供的主要服务
-
1.10.5.48.5.4 IP地址与域名
-
1.10.68.6 网络配置和安装
-
1.10.6.18.6.1 网络适配器的安装
-
1.10.6.28.6.2 安装TCP/IP协议
-
1.10.6.38.6.3 连接Internet
-
1.10.78.7 局域网的应用
-
1.10.7.18.7.1 共享设置
-
1.10.7.28.7.2 访问局域网
-
1.11第九章 Internet的使用
-
1.11.19.1 Internet信息浏览
-
1.11.1.19.1.1 IE的使用
-
1.11.1.29.1.2 其他浏览器介绍
-
1.11.29.2 使用outlook收发电子邮件
-
1.11.2.19.2.1 电子邮件
-
1.11.2.29.2.2 申请和使用电子邮件
-
1.11.2.39.2.3 用Outlook收发电子邮件
-
1.11.39.3 网络资源的查询
-
1.11.3.19.3.1 搜索引擎
-
1.11.3.29.3.2 著名搜索站点Google
-
1.11.3.39.3.3 3721中文网络实名
-
1.11.3.49.3.4 新浪网搜索引擎
-
1.11.49.4 网络资源信息下载
-
1.11.4.19.4.1 IE下载
-
1.11.4.29.4.2 用网际快车FlashGet下载文件
-
1.11.4.39.4.3 文件的压缩与解压缩
-
1.11.59.5 FTP客户端软件的使用
-
1.11.5.19.5.1 CuteFTP的启动及界面
-
1.11.5.29.5.2 站点管理器中的操作
-
1.11.5.39.5.3 连接站点
-
1.11.5.49.5.4 文件的上载(上传)与下载
-
1.11.69.6 网络的其他应用
-
1.11.6.19.6.1 网上通信
-
1.11.6.29.6.2 网上教育
-
1.11.6.39.6.3 电子商务
-
1.11.6.49.6.4 网上娱乐
-
1.11.6.59.6.5 网上医院
-
1.11.79.7 网页制作简介