1.4 计算机中的信息表示
1.4.1 进位计数制
数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。按进位的方法进行计数,称为进位计数制。
1.4.2 计算机中常用的数制
计算机中经常用到的数制有二进制、八进制、十进制和十六进制等。
1)二进制
二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发明。当前的计算机系统使用的基本上是二进制。
计算机内部采用二进制的原因:
①技术实现简单。计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开这两种状态正好可以用“1”和“0”表示。
②简化运算规则。两个二进制数和、积运算组合各有三种,运算规则简单,有利于简化计算机内部结构,提高运算速度。
③适合逻辑运算。逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
④易于进行转换。二进制与十进制数易于互相转换。
⑤用二进制表示数据具有抗干扰能力强、可靠性高等优点。因为每位数据只有高低两个状态,当受到一定程度的干扰时,仍能可靠地分辨出它是高还是低。
2)八进制
八进制是一种计数法,较二进制的数书写方便,常应用在电子计算机的计算中。
八进制表示法在早期的计算机系统中很常见,因此,偶尔还能看到人们使用八进制表示法。八进制适用于12位和36位计算机系统(或者其他位数为3的倍数的计算机系统)。但是,对于位数为2的幂(8位、16位、32位与64位)的计算机系统来说,八进制就不算很好了。因此,在过去几十年里,八进制渐渐地淡出了。不过,还是有一些程序设计语言提供了使用八进制符号来表示数字的能力,而且还有一些比较古老的Unix应用程序在使用八进制。
3)十进制
十进制计数法是相对二进制计数法而言的,是人们日常使用最多的计数方法(俗称“逢十进一”),即“每相邻的两个计数单位之间的进率都为十”。
4)十六进制
十六进制是计算机中数据的一种表示方法,同人们日常中的十进制表示法不一样。它由数字0-9和字母A-F组成,与10进制的对应关系是:0-9对应0-9;A-F对应10-15。
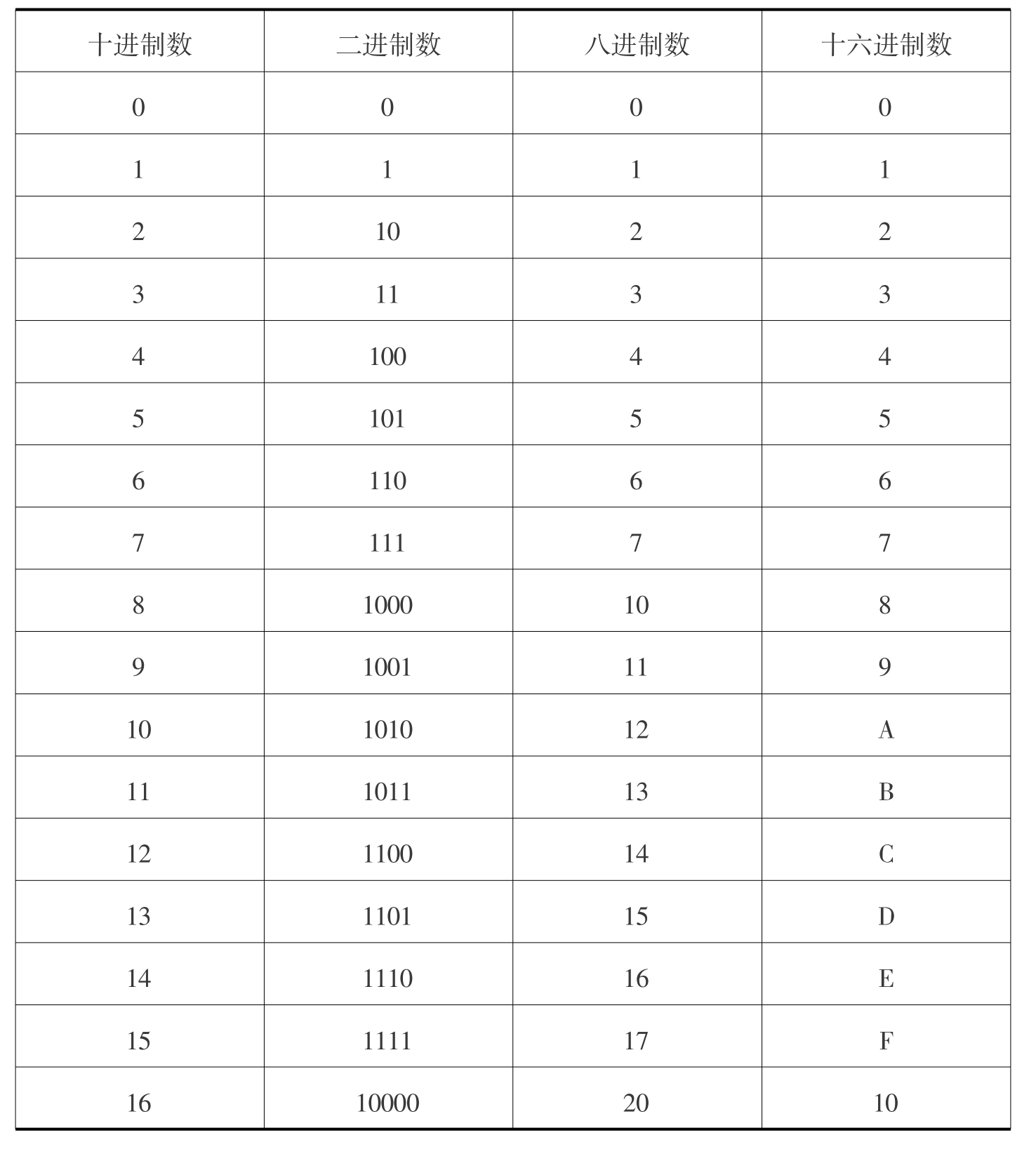
二进制、八进制、十进制和十六进制之间的特点对比如表1.1所示,数值对比如表1.2所示。
表1.1 二进制、八进制、十进制和十六进制特点对比
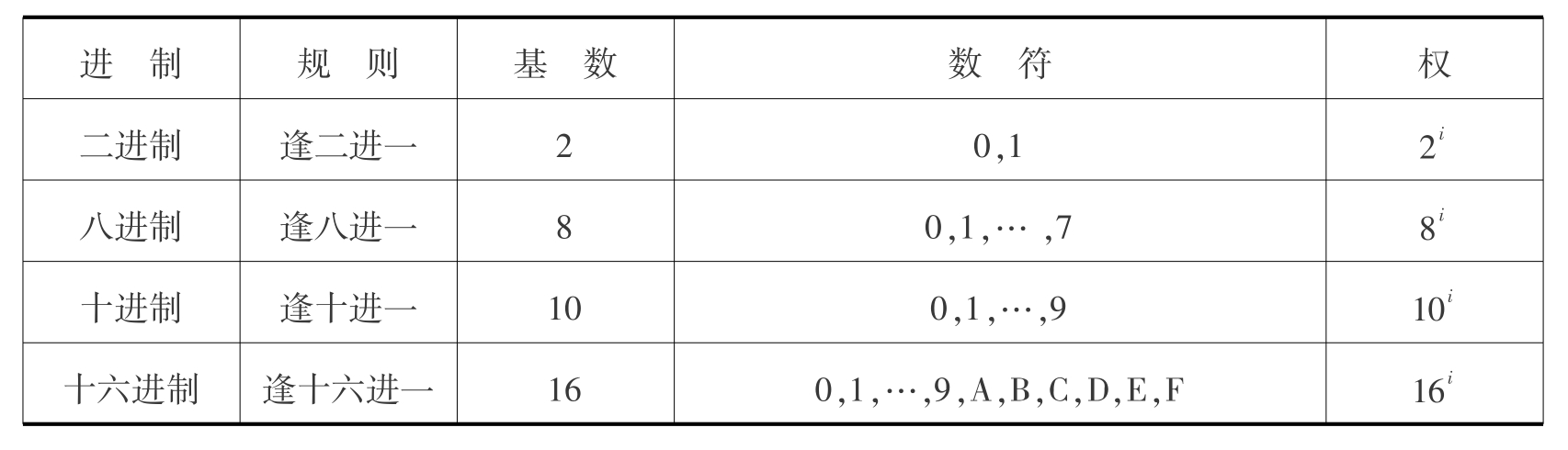
表1.2 常用计数制的表示方法
1.4.3 数制转换
这里主要讨论二进制、八进制、十进制和十六进制数之间的相互转换,并用R表示进制的基数。
1)书写规则
为了区分各种计数制的数,常采用如下方法进行书写。
(1)在数字后面加写相应的英文字母作为标志
B(Binary)表示二进制数。二进制数的100可写成100B。
O(Octonary)表示八进制数。八进制数的100可写成100O。
D(Decimal)表示十进制数。十进制数的100可写成100D。
H(Hexadecimal)表示十六进制数。十六进制数100可写成100H。
一般约定D可省略,即无后缀的数字为十进制数字。
(2)在括号外面加数字下标
(1101)2表示二进制数的1101。
(3174)8表示八进制数的3174。
(6678)10表示十进制数的6678。
(2DF6)16--表示十六进制数的2DF6。
2)R进制数转换为十进制数
要将R进制数转换为十进制数,只要把它们各位按权展开求和即可。
二进制转换成十进制:
(110.1101)2
=1×22+1×21+0×20+1×2-1+1×2-2+0×2-3+1×2-4
=4+2+0+0.5+0.25+0+0.0625
=(6.8125)10
八进制转换成十进制:
(423.2)8
=4×82+2×81+3×80+2×8-1
=256+16+3+0.25
=(275.25)10
十六进制转换成十进制:
(3A.B)16
=3×161+10×160+11×16-1
=48+10+0.6875
=(58.6875)10
3)十进制数转换为R进制数
要将十进制数转换为等值的二进制、八进制和十六进制数,需要对整数部分和小数部分分别进行转换。
整数部分:连续除以基数R,直到商为0为止,再逆序取各位余数。
小数部分:连续乘基数R,直到积为整数为止,再顺序取各位整数。
例如:
(100.6875)10=(1100100.1011)2

(100)10=(144)8=(64)16
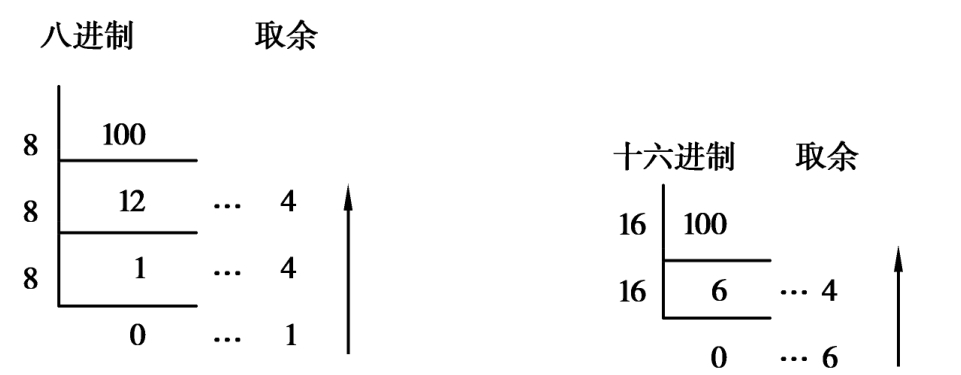
4)二进制数、八进制数和十六进制数之间的相互转换
二进制数、八进制数和十六进制数之间的相互转换很有实用价值。由于这3种进制的权之间有内在的联系,即23=8,24=16,因此它们之间的转换比较容易,即每位八进制数相当于3位二进制数,每位十六进制数相当于4位二进制数。
在转换时,位组划分是以小数点为中心向左右两边进行的,中间的0不能省略,两头不足时可以补0。例如将(11101.00101)2转换成八进制数:
011 101.001 010
3 5 1 2 (11101.00101)2=(35.12)8
由二进制转换为十六进制与由二进制转换为八进制的方法一样,只不过每四位为一组。如将(11101.00101)2转换成十六进制数:
0001 1101.0010 1000
1 D 2 8(11101.00101)2=(1D.28)16
在由八、十六进制转换成二进制的数时,将每一位上的数字转换成一个四位的二进制数,然后将这些二进制数组合。如将(F28)16转换成二进制数:
F 2 8
1111 0010 1000 (F28)16=(111100101000)2
将(72.46)8转换成二进制数:
7 2 4 6
111 010 100 110 (72.46)8=(111010.100110)2
如果要将八进制数转换成等值的十六进制数,可以先将八进制数转换成二进制数,再把二进制数转换成十六进制数,反之亦然。例如:(32)8=(011010)2=(1A)16。
5)计算机存储和处理二进制数的常用单位
在计算机内部,一切数据都用二进制形式来表示。为了衡量计算机中数据的量,人们规定了一些二进制数的常用单位,如位、字节等。
(1)位(bit)
位是二进制数中的一个数位,可以是“0”或“1”。它是计算机中数据的最小单位,称为比特(bit)。
(2)字节(Byte)
通常将8位二进制数组成一组,称作一个字节。字节是计算机中数据处理和存储容量的基本单位,如存放一个英文字母需要在存储器中占用一个字节的空间。书写时,常将字节英文单词Byte简写成B,这样:
1B=8bit
常用的单位还有KB(千字节)、MB(兆字节)、GB(千兆字节)、TB(万亿字节)等,它们之间的关系是:
1B=8bit
1KB=1024B=210B
1MB=1024KB=220B
1GB=1024MB=230B
1TB=1024GB=240B
1.4.4 数值数据的编码
数值型数据有大小、正负之分,能够进行算术运算,如552、-345.17、1/3等。如何用“0”“1”描述正负号、小数点等问题呢?在计算机内将数值型数据全面、完整地表示成一个二进制数(机器数),应该考虑三个因素:机器数的范围、机器数的符号和机器数中小数点的位置。
1)机器数的范围
机器数的表示范围由硬件(CPU中的寄存器)决定。当使用8位寄存器时,字长为8位,所以一个无符号整数的最大值是(11111111)2=(255)10,机器数的范围为0~255;当使用16位寄存器时,字长为16位,所以一个无符号整数的最大值是(FFFF)16=(65535)10,机器数的范围为0~65535。
2)机器数的符号
在计算机内部,任何数据都只能用二进制的两个数码“0”和“1”来表示。正负数的表示也不例外,除了用“0”和“1”的组合来表示数值的绝对值大小外,其正负号也必须用0和1的形式表示。通常规定最高位为符号位,并用0表示正,用1表示负。这时在一个8位字长的计算机中,数据的格式如图1.13所示。

图1.13 机器数的符号
最高位D7为符号位,D6~D1为数值位。这种把符号数字化并和数值位一起编码的方法,很好地解决了带符号数的表示方法及其计算问题。这类编码方法常用的有原码、反码、补码三种。
原码表示法规定:最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
原码10010110=反码11101001(最高位为1,此数为一负数)
(11101010)2=(-106)10
补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
在计算机中,小数点位置固定的数称为定点数。通常,计算机中的定点数有两种:定点整数和定点小数。
3)定点数和浮点数
在计算机内部难以表示小数点,故小数点的位置是隐含的。隐含的小数点位置可以是固定的,也可以是变动的,前者称为“定点数”,后者称为“浮点数”。
(1)定点数
在定点数中,小数点的位置一旦固定,就不再改变。定点数中又有定点整数和定点小数之分。
定点整数,小数点的位置约定在最低位的右边,用来表示整数;定点小数,小数点的位置约定在符号位之后,用来表示小于1的纯小数。
例如:设机器的定点数长度为2个字节,用定点整数表示(194)10。
因为(194)10=11000010B,故机器内表示形式如图1.14所示。
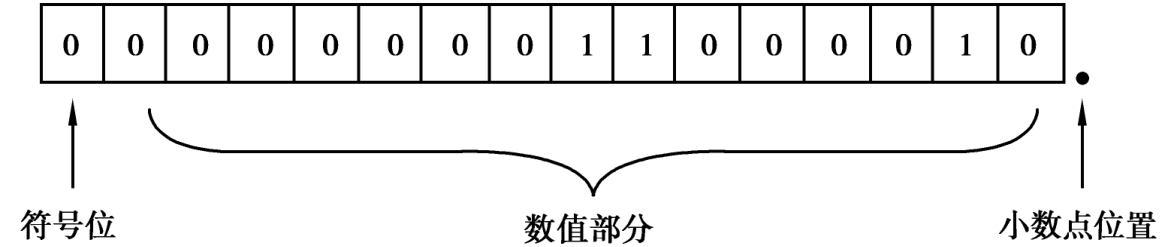
图1.14 机器内的定点整数
例如:用定点小数表示(-0.6875)10。
因为,(-0.6875)10=-0.101100000000000B,其机内表示如图1.15所示。
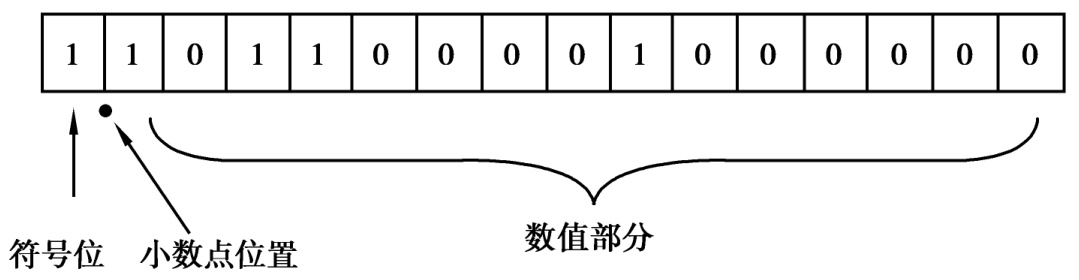
图1.15 机器内的定点小数
(2)浮点数
如果要处理的数既有整数部分,又有小数部分,采用定点数便会遇到麻烦。为此引出浮点数,即小数点位置不固定。
将十进制数66.37、-6.637、0.6637、-0.06637用指数形式表示,它们分别可以表示为:0.6637×102、-0.6637×101、0.6637×100、-0.6637×10-1。
可以看出,在原数字中无论小数点前后各有几位数,它们都可以用一个纯小数(称为尾数,有正、负)与10的整数次幂(称为阶数,有正、负)的乘积形式来表示,这就是浮点数的表示法。
同理,一个二进制数N也可以表示为:N=±S×2±P。
式中的N、P、S均为二进制数。S称为N的尾数,即全部的有效数字(数值小于1),S前面的±号是尾数的符号;P称为N的阶码(通常是整数),即指明小数点的实际位置,P前面的±号是阶码的符号。
计算机中一般浮点数的存放形式如图1.16所示。

图1.16 浮点数的存放形式
在浮点数表示中,尾数的符号和阶码的符号各占一位;阶码是定点整数,阶码的位数决定了所表示的数的范围;尾数是定点小数,尾数的位数决定了数的精度。
1.4.5 字符编码
字符是计算机中使用最多的非数值型数据,如英文字母、不做算术运算的数字、可印刷的符号、控制符号等。它是人与计算机进行通信、交互的重要媒介。在计算机内部,可以采用不同的编码方式对字符进行二进制编码。当用户输入一个字符时,系统自动将用户输入字符按编码的类型转换为相应的二进制形式存入计算机存储单元中;在输出过程中,再由系统自动将二进制编码数据转换成用户可以识别的数据格式输出给用户。编码方式主要有如下几种:
1)ASCII码
目前计算机中使用最广泛的字符编码是ASCII码,即美国标准信息交换码(American Standard Code for Information Interchange)。ASCII包括32个通用控制字符、10个十进制数码、52个英文大小写字母和34个专用符号,共128个元素,故需要用7位二进制数进行编码,以区分每个字符。通常使用一个字节(即8个二进制位)表示一个ASCII码字符,规定其最高位总是0。ASCII码见表1.3。
表1.3 标准七位ASCII码字符集
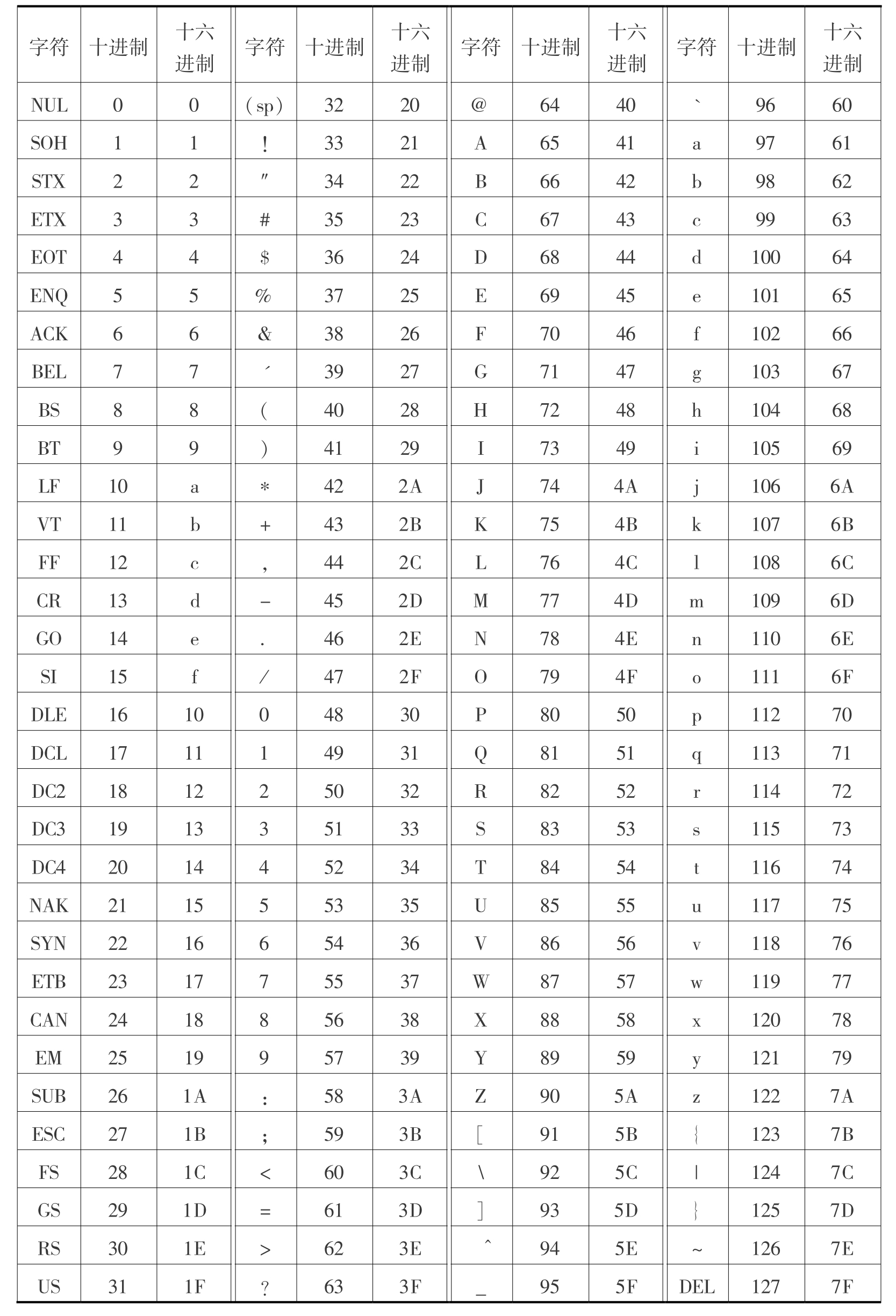
在这128个ASCII码字符中,编码0-31是32个不可打印和显示的控制字符,其余96个编码则对应着键盘上的字符。除编码32和128这两个字符不能显示出来之外,另外94个字符均为可以显示的字符。从表1.3中可以看出以下规律:
①数字0的ASCII码是48D或30H;大写字母A的ASCII码是65D或41H;小写字母a的ASCII码是97D或61H。
②数字0-9、大写字母A-Z、小写字母a-z之间的ASCII码值是连续的。因此,如果知道了数字0、大写字母A和小写字母a的ASCII码值,就可以推算出所有数字和字母的ASCII码值。例如:A的ASCII码为1000001,对应的十进制数是65,由A-Z编码连续可以推算出字母D的ASCII码是68(十进制数)。
③数字0-9的ASCII码值小于所有字母的ASCII码值;大写字母的ASCII码值小于小写字母的ASCII码值;大写字母与其对应的小写字母之间的ASCII码值之差正好是十进制数32。
2)BCD码
BCD(Binary Coded Decimal)码又称“二唱十进制编码”,专门解决用二进制数表示十进制数的问题。“二唱十进制编码”方法很多,有8421码、2421码、5211码、余3码、右移码等。最常用的是8421编码,其方法是用四位二进制数表示一位十进制数,自左至右每一位对应的位权是8、4、2、1。四位二进制数有0000-1111共16种状态,而十进制数只有0-9十个数码,所以,BCD码只取0000-1001十种状态,其余6种不用。8421编码见表1.4所示。
表1.4 8421编码表
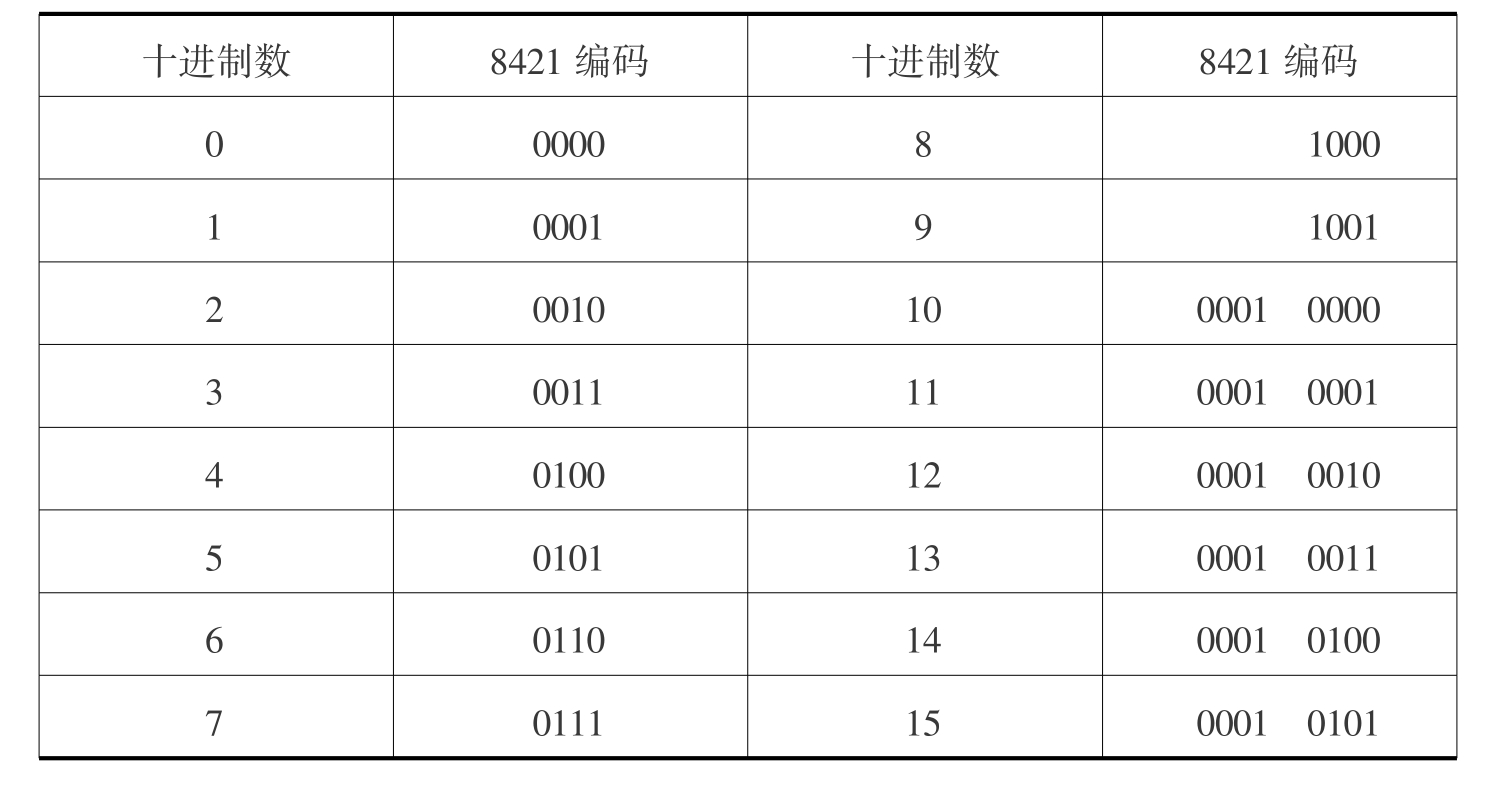
由于BCD码中的8421编码应用最广泛,所以经常将8421编码混称为BCD码,也为人们所接受。如十进制数5803的8421编码:0101 1000 0000 0011。
由于需要处理的数字符号越来越多,为此又出现“标准六位BCD码”和八位的“扩展BCD码”(EBCDIC码)。在BCDIC码中,除了原有的10个数字之外,又增加了一些特殊符号,如大、小写英文字母和某些控制字符。
3)汉字编码
汉字的输入、转换、传输和存储方法与英文相似,但是由于汉字数量多,一般不能由键盘直接输入,所以汉字的编码和处理相对英文要复杂得多。经过多年的努力,我国在汉字信息处理的研制和开发方面取得了突破性进展,使我国的汉字信息处理技术处于世界领先地位。汉字通常用两个字节进行编码,且根据传输、输入、存储和处理、打印或显示等不同处理场合,分为交换码、输入码、机内码和字型码。
(1)交换码
不同设备之间交换信息需要有共同的信息表示方法,对于字符和汉字的交换也需要制定一种人们共同遵守的编码标准,这就是交换码标准。现在,汉字交换码主要采用国标码和BIG5码两种编码方式。
①国标码。1981年我国公布的枟通用汉字字符集(基本集)及其交换码标准枠GB2312-80编码简称国标码,它规定每个汉字编码由两个字节构成。第一个字节的范围为A1H-FEH,共94种,第二个字节的范围也为A1H-FEH,共94种。利用这两个字节可定义出94×94=8836种汉字,实际共定义了6763个汉字和682个图形符号。汉字分为两级,即一级(常用)汉字3755个(按汉语拼音排序)和二级(次常用)汉字3008个(按偏旁部首排序)。
为了满足信息处理的需要,在国标码的基础上,2000年3月我国又推出了枟信息技术·信息交换用汉字编码字符集·基本集的扩充枠新国家标准,共收录了27000多个汉字,还包括藏、蒙、维吾尔等主要少数民族文字,采用单、双、四字节混合编码,基本上解决了计算机汉字和少数民族文字的使用标准问题。
②BIG5码。BIG5码是台湾计算机界实行的汉字编码字符集。BIG5码规定:每个汉字编码由两个字节构成,第一个字节的范围为A1H-F9H,共89种,第二个字节的范围分别为40H-7EH,A1H-FEH,共157种。也就是说,利用这两个字节共可定义出89×157=13973种汉字,其中,常用字共5401个,次常用字共7652个,剩下的便是一些特殊字符。
(2)汉字输入码
在计算机系统处理汉字时,首先遇到的问题是如何输入汉字。汉字输入码也称“外码”,是为将汉字输入到计算机设计的代码。汉字输入码种类较多,选择不同的输入码方案,则输入的方法及按键次数、输入速度均有所不同。综合起来,汉字输入码主要有:数字编码,如区位码;拼音码,如全拼输入法、微软拼音输入法、紫光输入法、搜狗拼音输入法、智能ABC输入法等;形码,如五笔字型输入法、表形码;音形码,如双拼码、五十字元等。
(3)汉字机内码
汉字机内码,又称“汉字ASCII码”,简称“内码”,指计算机内部存储、处理加工和传输汉字时所用的由0和1符号组成的代码。输入码被接受后就由汉字操作系统的“输入码转换模块”转换为机内码,与所采用的键盘输入法无关。机内码是汉字最基本的编码,不管是什么汉字系统和汉字输入方法,输入的汉字外码到机器内部都要转换成机内码才能被存储和进行各种处理。
一般要求机内码与国标码之间有较简单的转换规则,通常将国标码的前两个字节的最高位置“1”作为汉字的机内码。以汉字“啊”为例,其机内码为B0A1H,即10110000 10100001。
(4)汉字字型码
汉字字型又称汉字字模,用于汉字在显示屏或打印机输出。汉字字型码通常有两种表示方式:点阵和矢量。
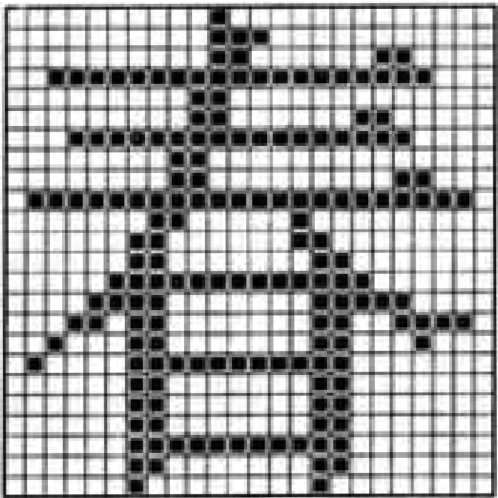
图1.17 汉字点阵表示法
用点阵表示字型时,汉字字型码指的是这个汉字字型点阵的代码。根据输出汉字的要求不同,点阵的多少也不同。简易型汉字为16*16点阵,提高型汉字为24*24点阵、32*32点阵、48*48点阵等。点阵规模愈大,字型愈清晰美观,所占存储空间也愈大,如图1.17所示。
矢量表示方式存储的是描述汉字字型的轮廓特征,当要输出汉字时,通过计算机的计算,由汉字字型描述生成所需大小和形状的汉字点阵。矢量化字型描述与最终文字显示的大小、分辨率无关,因此可以产生高质量的汉字输出。Windows中使用的True Type技术就是汉字的矢量表示方式。
4)各种编码之间的关系
各种汉字编码使用的场合及其之间的关系如图1.18所示。汉字通常通过汉字输入码并借助输入设备输入到计算机内,再由汉字系统的输入管理模块进行查表或计算,将输入码(外码)转换成机器内码存入计算机存储器中。当存储在计算机内的汉字需要在屏幕上显示或在打印机上输出时,要借助汉字机内码在字模库中找出汉字的字型码,在输出设备上将该汉字的图形信息显示出来。当要与其他设备进行信息交换时,需要进行机内码和交换码之间的转换。
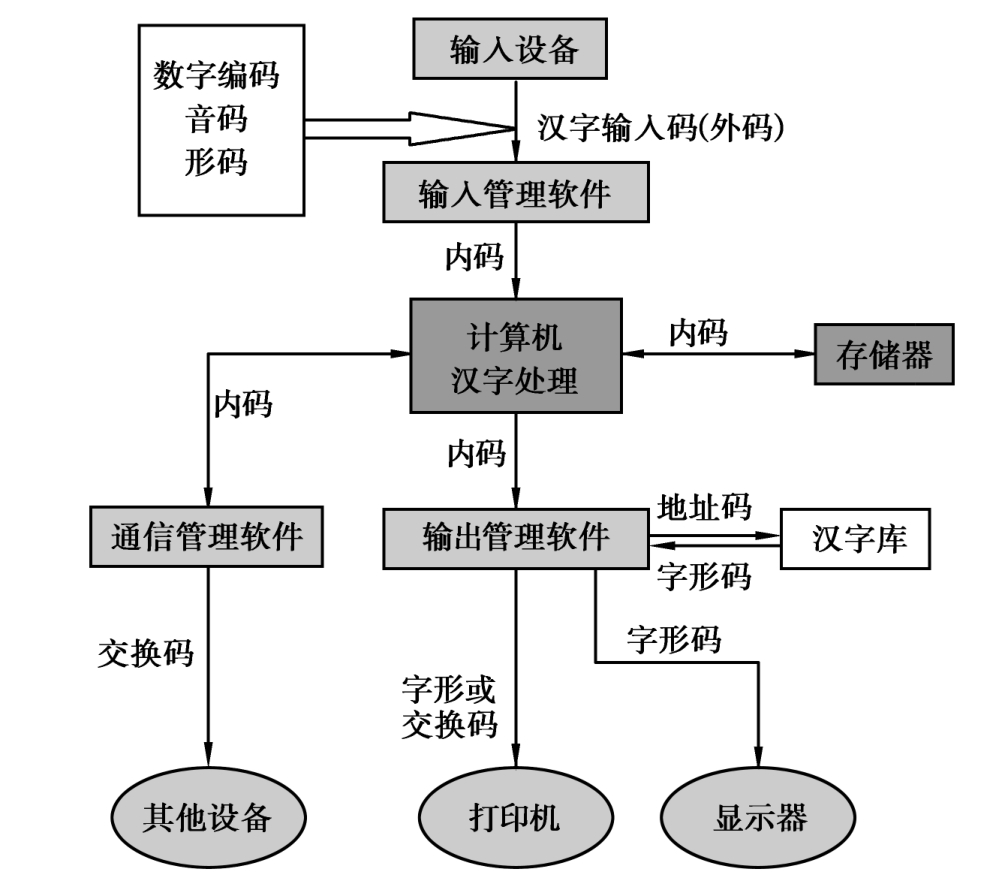
图1.18 各种编码之间的关系










