-
1.1高等学校广义建筑学系列教材编委会
-
1.2内容简介
-
1.3序
-
1.4前 言
-
1.5第1章 建筑构造概述
-
1.5.1§1.1 建筑构造课程的内容及要求
-
1.5.2§1.2 建筑的构造组成部分及作用
-
1.5.3§1.3 建筑物的分类
-
1.5.4§1.4 建筑构造的影响因素及建筑标准化
-
1.5.5复习思考题1
-
1.6第2章 基础与地下室构造
-
1.6.1§2.1 基础与地基的关系
-
1.6.2§2.2 基础的分类及构造
-
1.6.3§2.3 地下室构造
-
1.6.4复习思考题2
-
1.7第3章 墙体
-
1.7.1§3.1 墙体的类型和设计要求
-
1.7.2§3.2 块材墙体构造
-
1.7.3§3.3 隔墙与隔断构造
-
1.7.4§3.4 外墙的保温与隔热
-
1.7.5复习思考题3
-
1.8第4章 楼板层和地坪构造
-
1.8.1§4.1 楼板的类型及设计要求
-
1.8.2§4.2 钢筋混凝土楼板层
-
1.8.3§4.3 楼地面构造
-
1.8.4§4.4 顶棚装饰构造
-
1.8.5§4.5 阳台与雨篷
-
1.8.6复习思考题4
-
1.9第5章 楼梯与其他垂直交通设施
-
1.9.1§5.1 楼梯的组成、类型、尺度
-
1.9.2§5.2 预制装配式钢筋混凝土楼梯构造
-
1.9.3§5.3 现浇整体式钢筋混凝土楼梯构造
-
1.9.4§5.4 楼梯的细部构造
-
1.9.5§5.5 室外台阶与坡道
-
1.9.6§5.6 电梯与自动扶梯
-
1.9.7复习思考题5
-
1.10第6章 门和窗
-
1.10.1§6.1 门和窗概述
-
1.10.2§6.2 窗的种类与构造
-
1.10.3§6.3 门
-
1.10.4§6.4 特殊门、窗构造
-
1.10.5§6.5 遮阳
-
1.10.6复习思考题6
-
1.11第7章 屋顶
-
1.11.1§7.1 屋顶概述
-
1.11.2§7.2 屋顶排水设计
-
1.11.3§7.3 平屋顶设计
-
1.11.4§7.4 坡屋顶设计
-
1.11.5§7.5 屋顶的保温与隔热
-
1.11.6复习思考题7
-
1.12第8章 变形缝
-
1.12.1§8.1 伸缩缝
-
1.12.2§8.2 沉降缝
-
1.12.3§8.3 防震缝
-
1.12.4§8.4 设变形缝处建筑物的结构布置
-
1.12.5复习思考题8
-
1.13第9章 正投影图的基本知识
-
1.13.1§9.1 投影图的概念与分类
-
1.13.2§9.2 正投影的基本性质
-
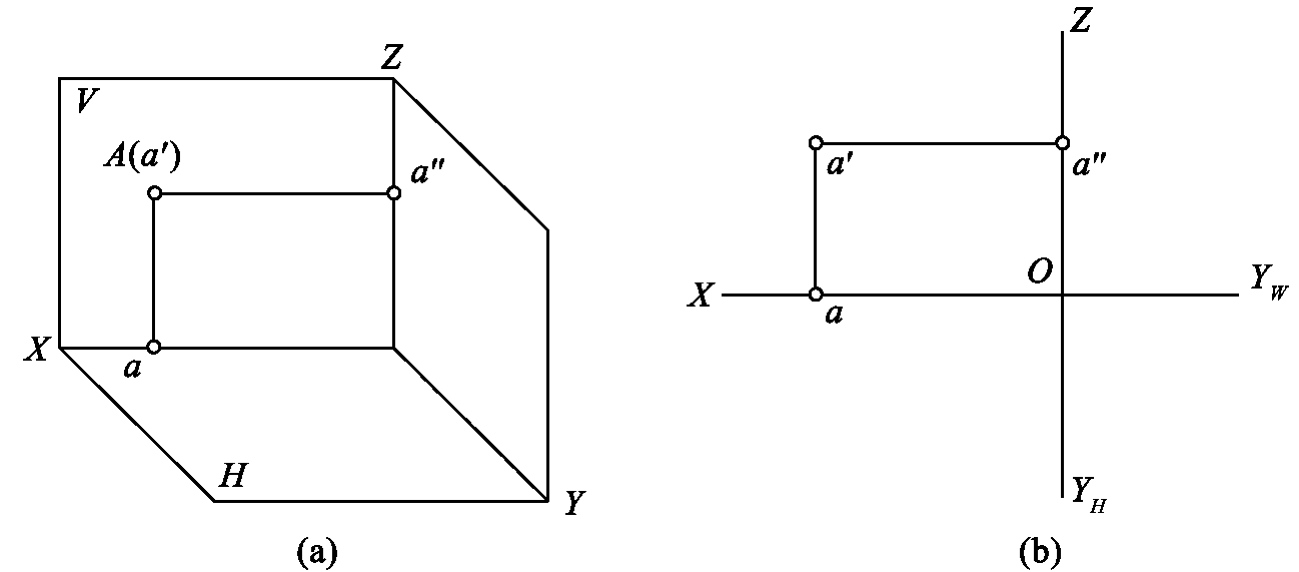
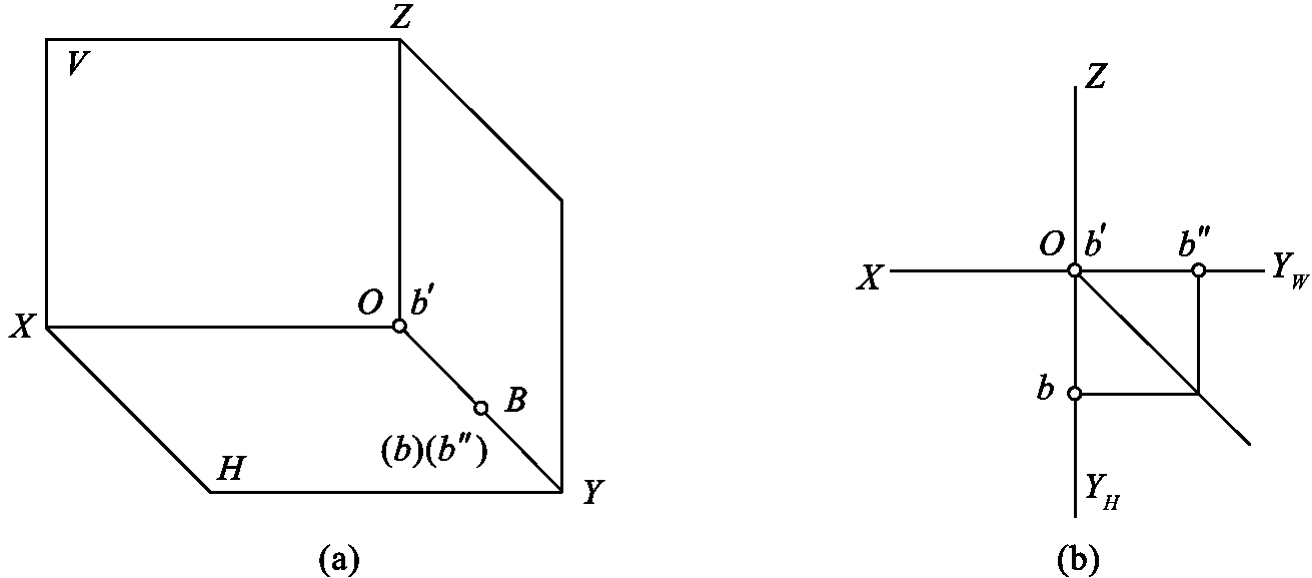
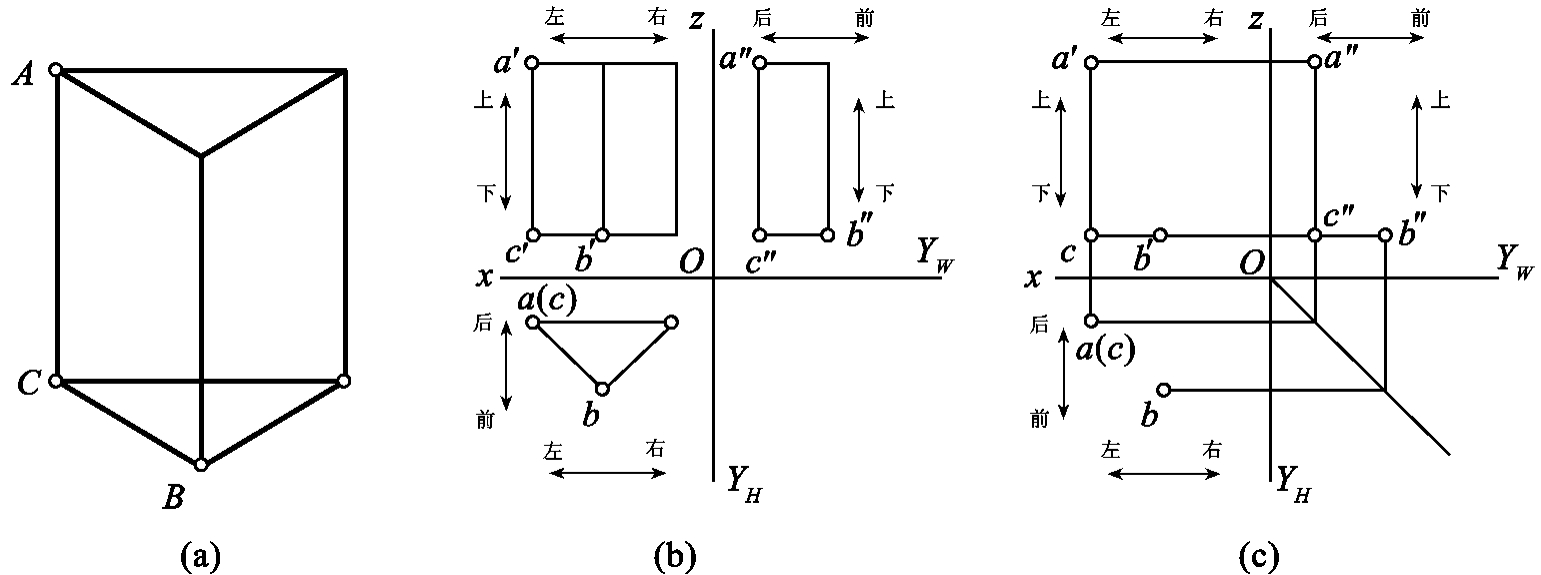
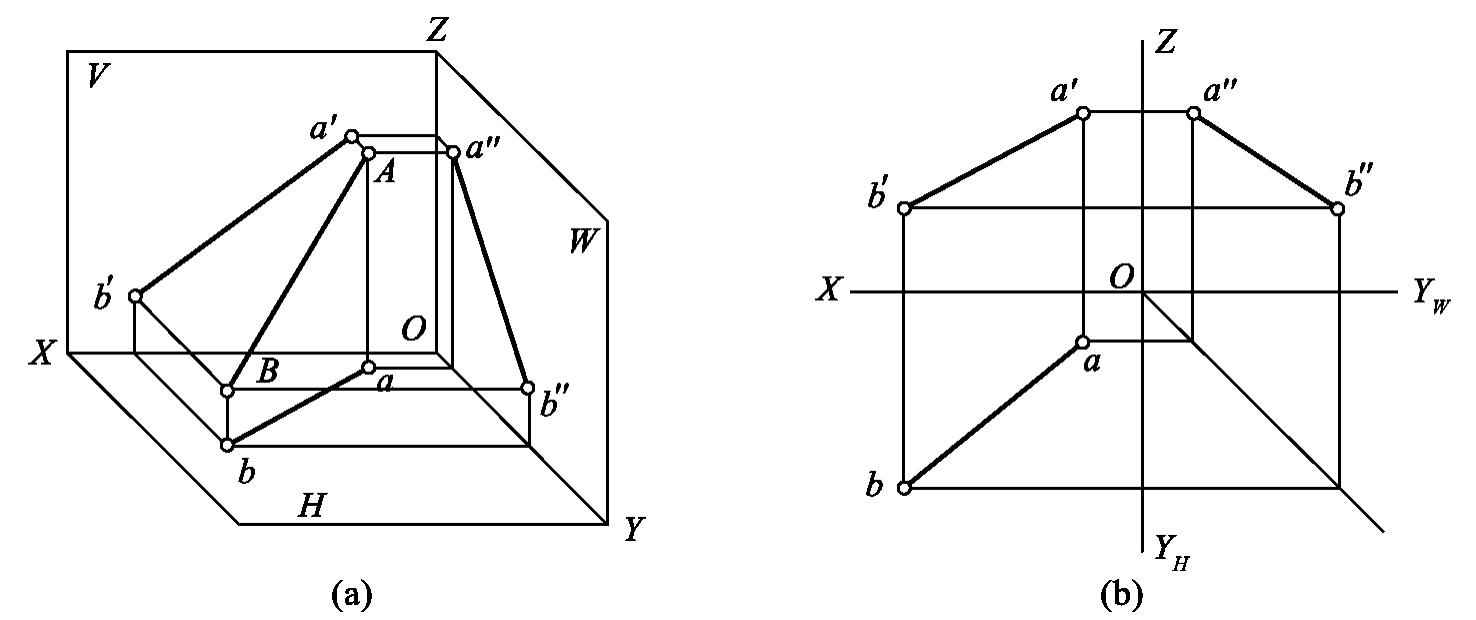
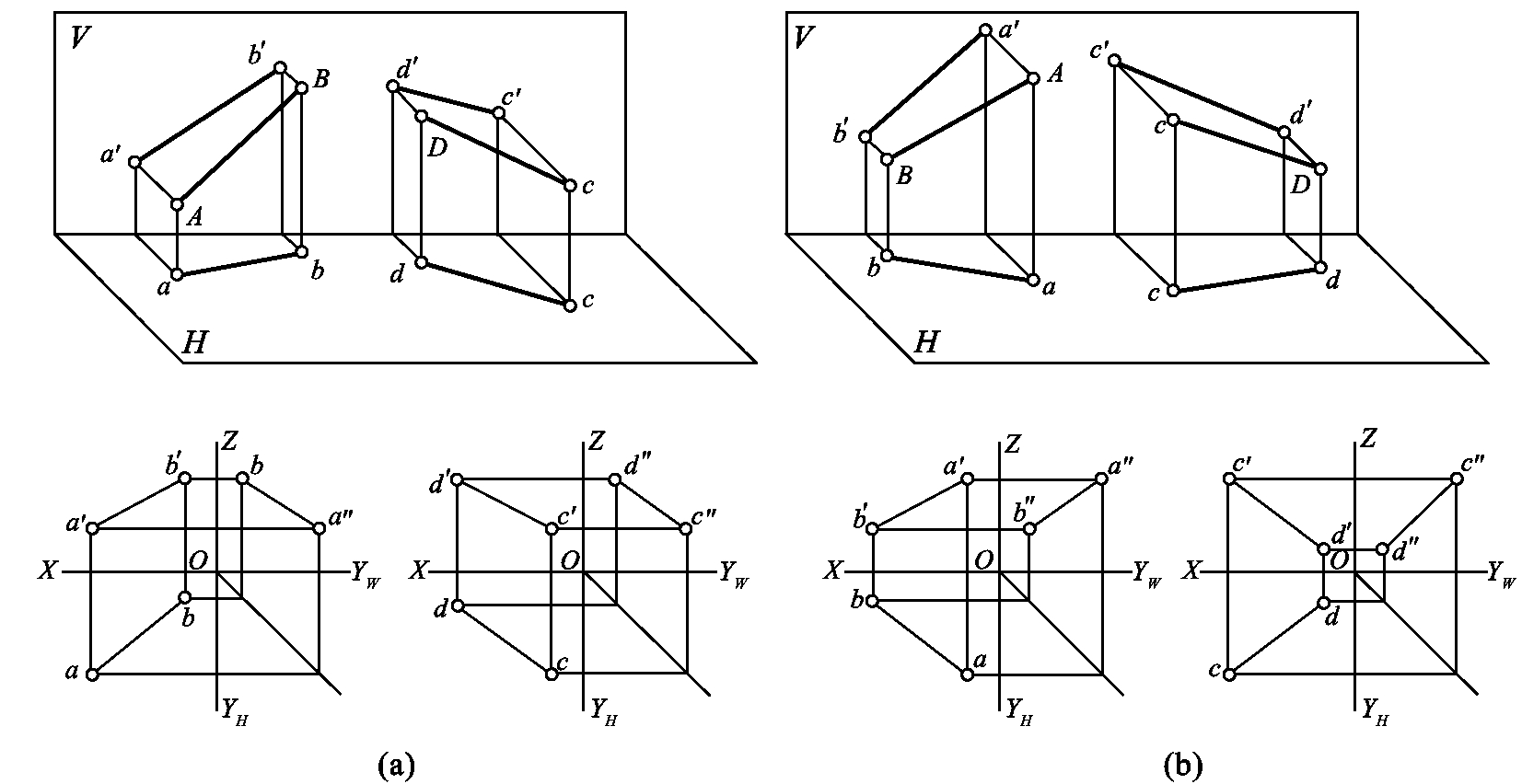
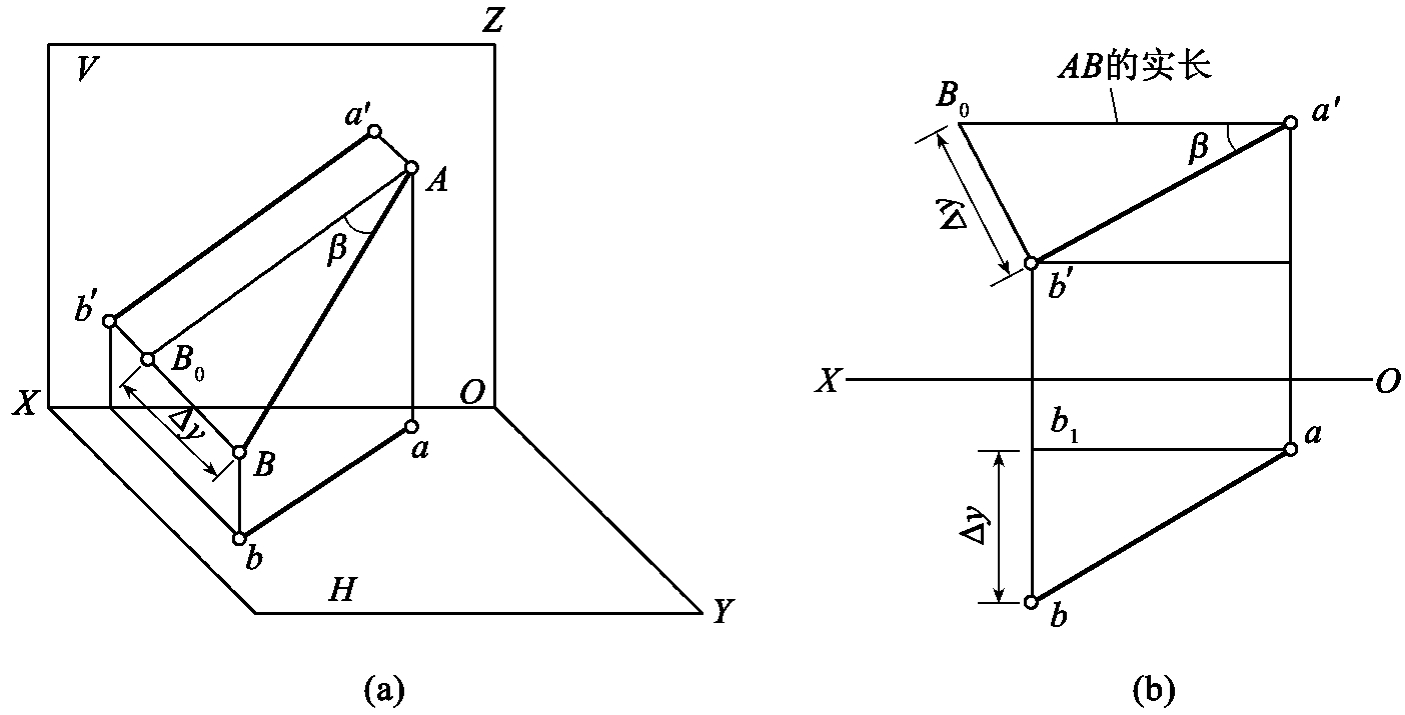
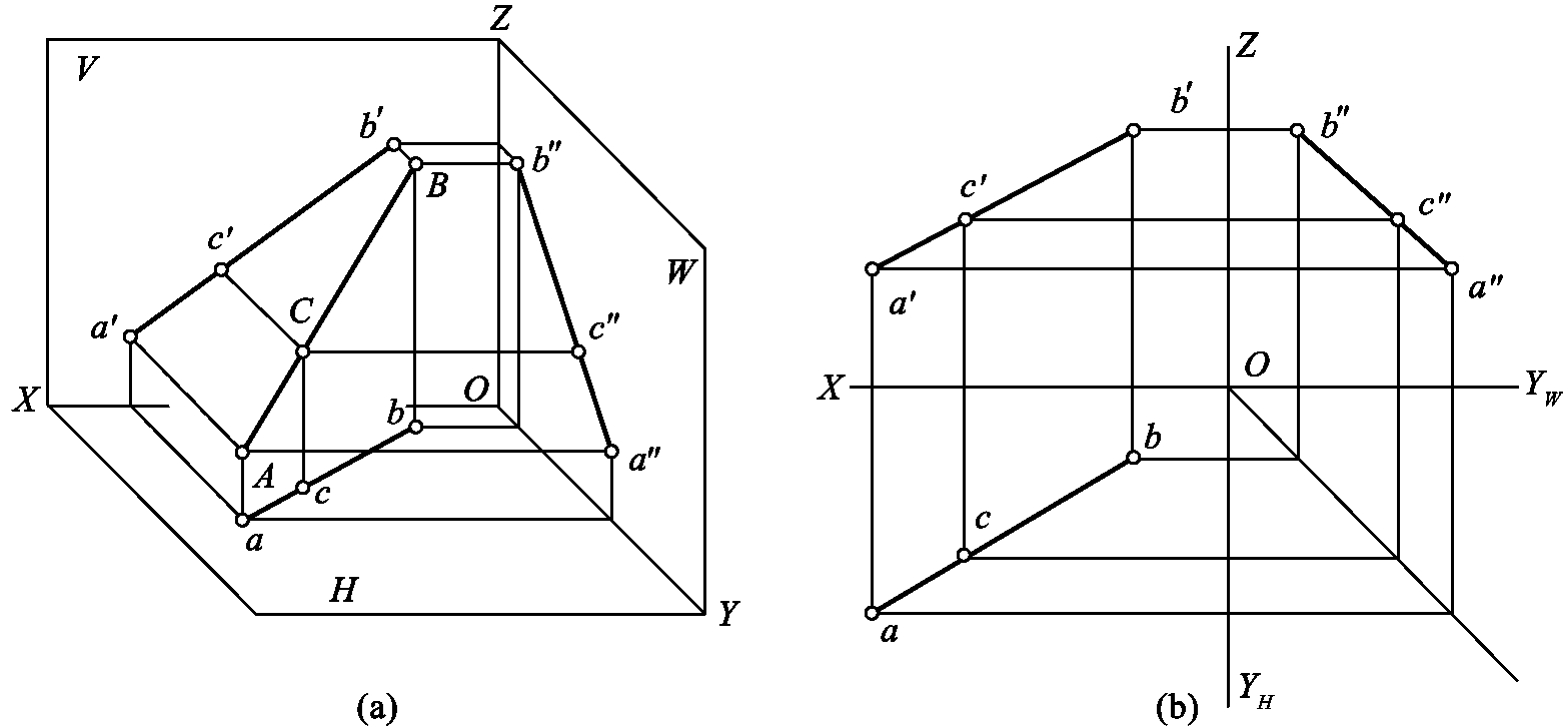
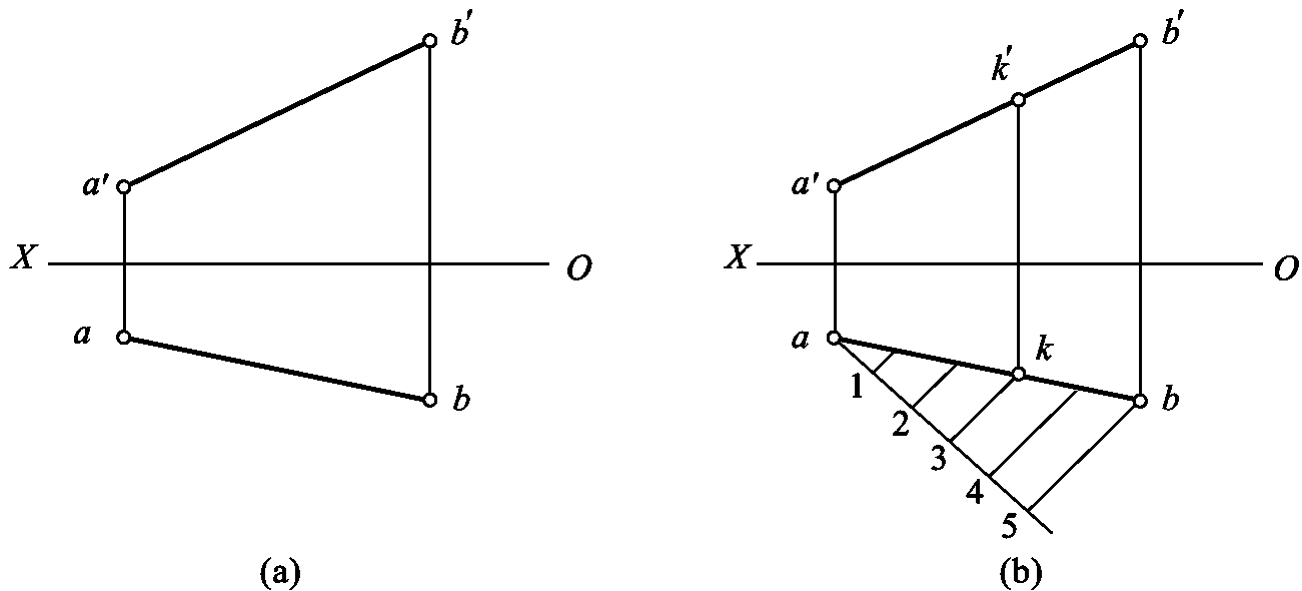
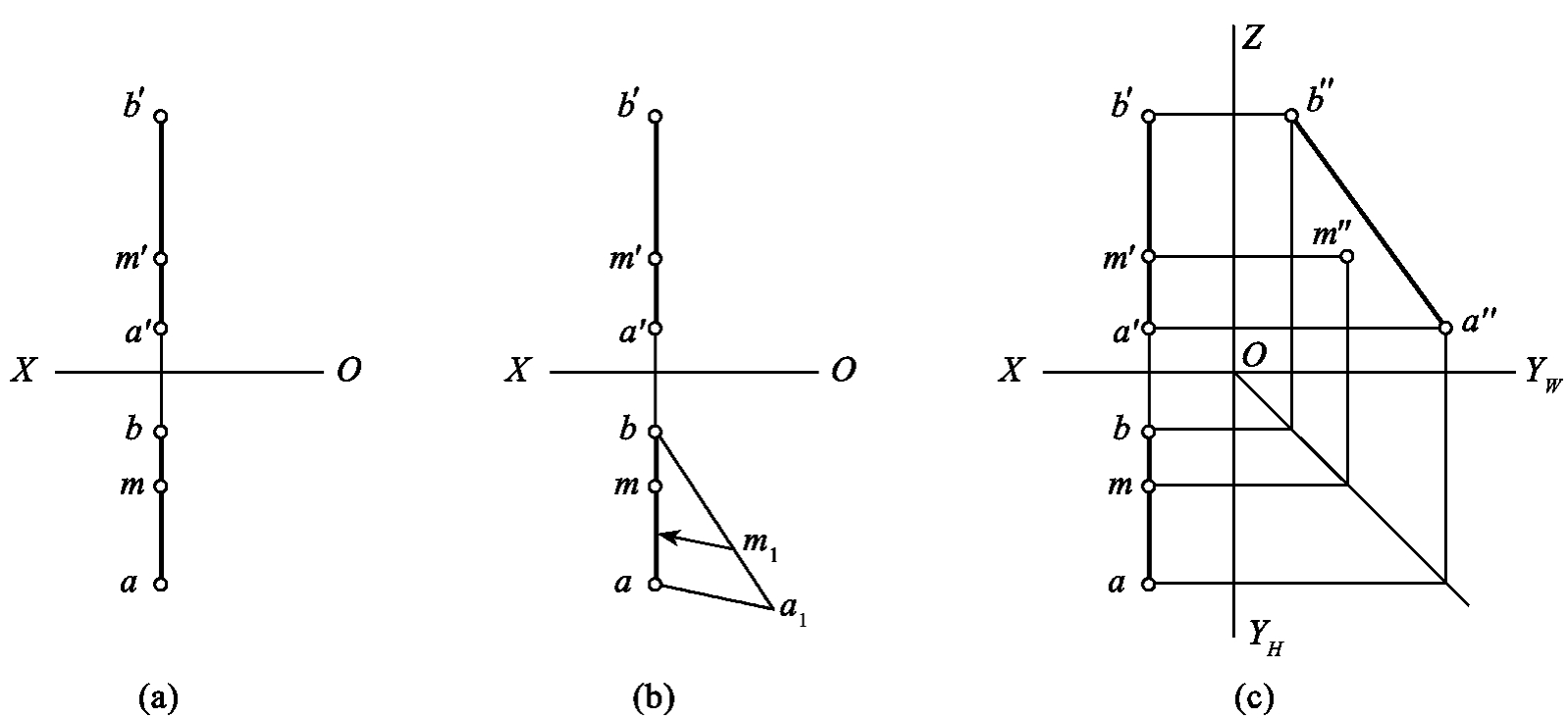
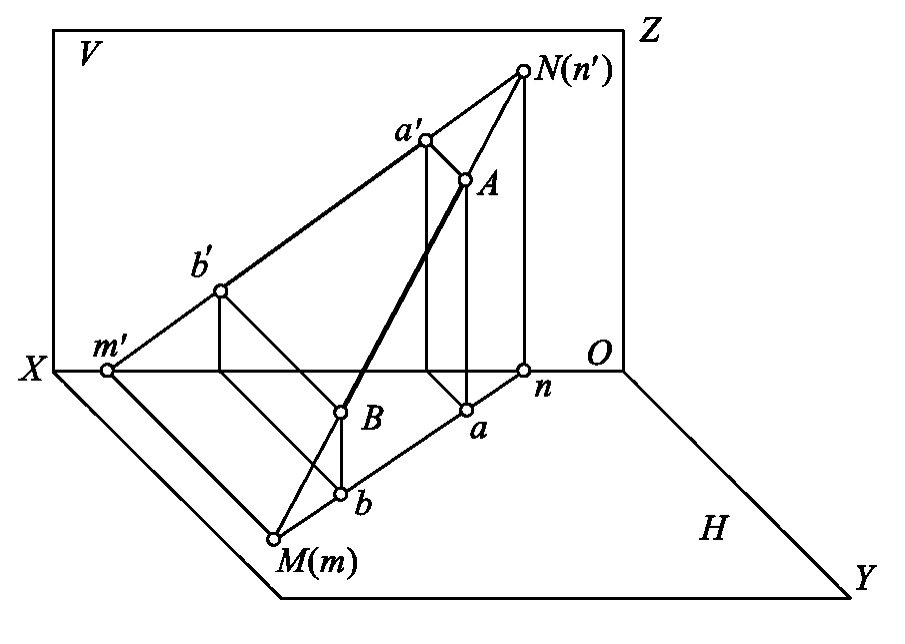
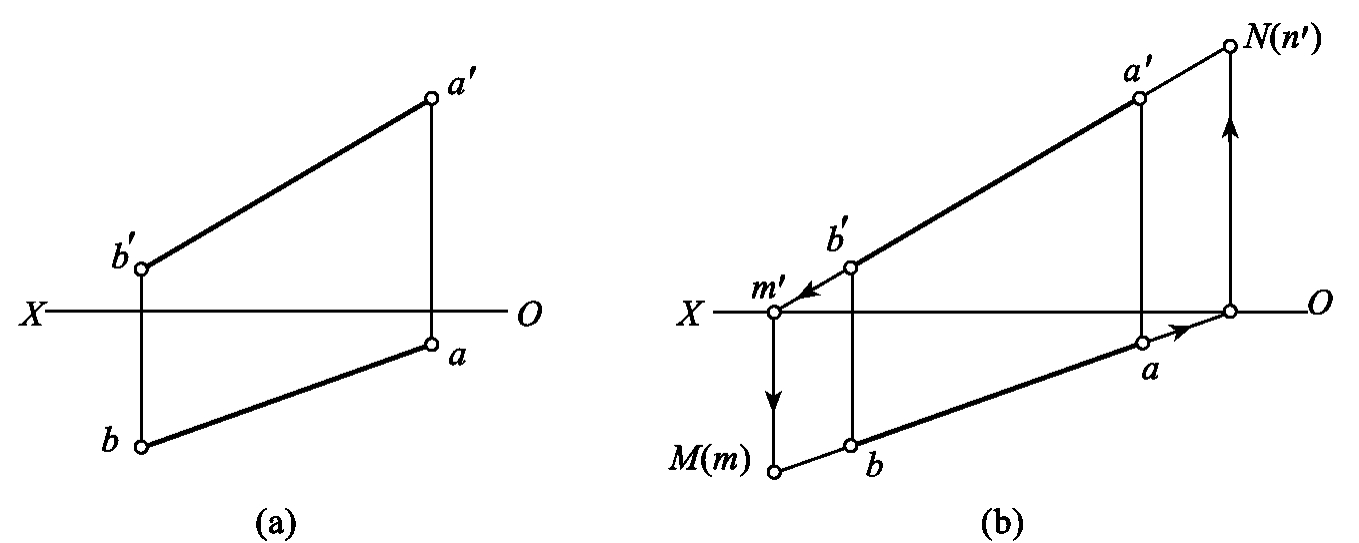
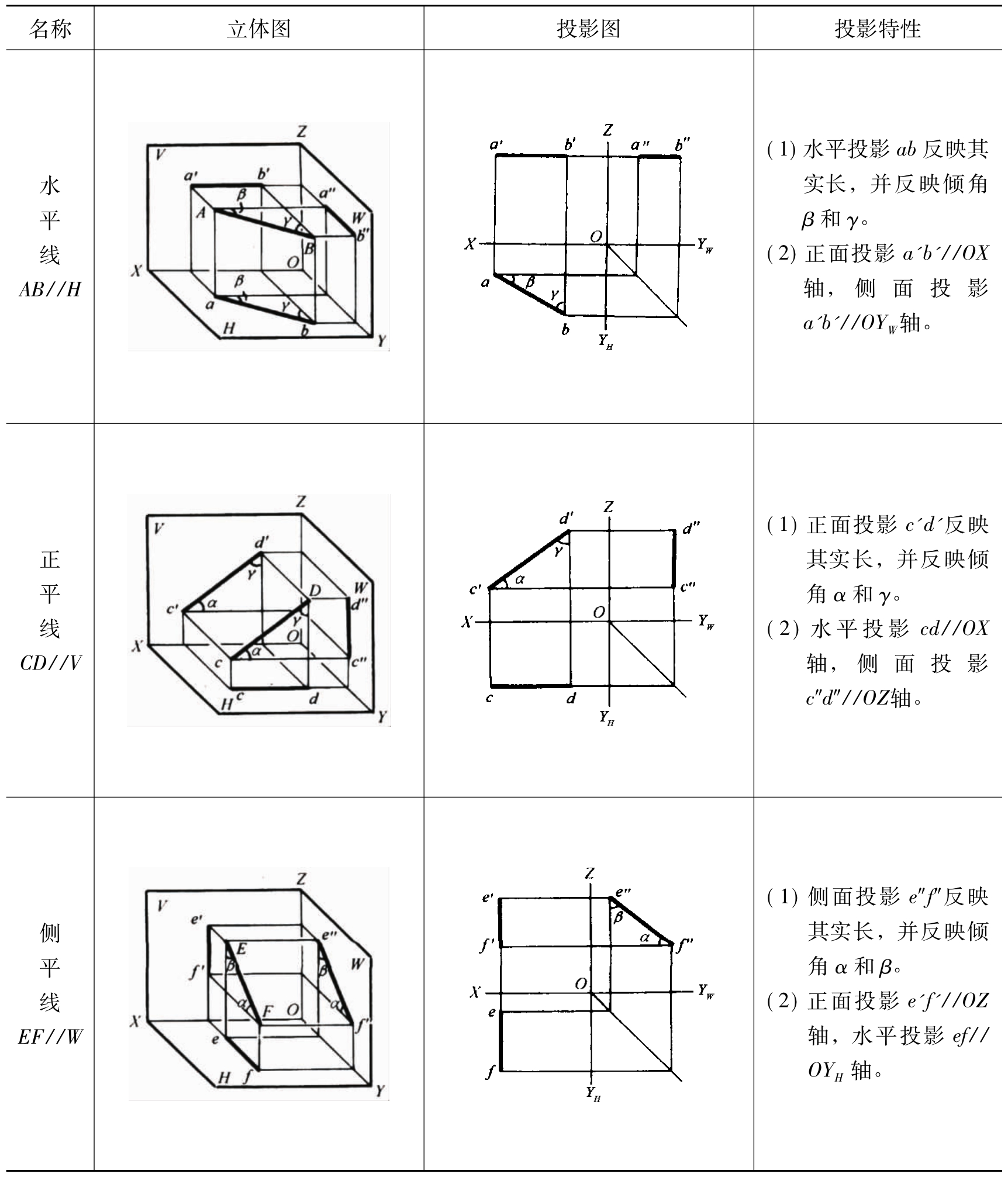
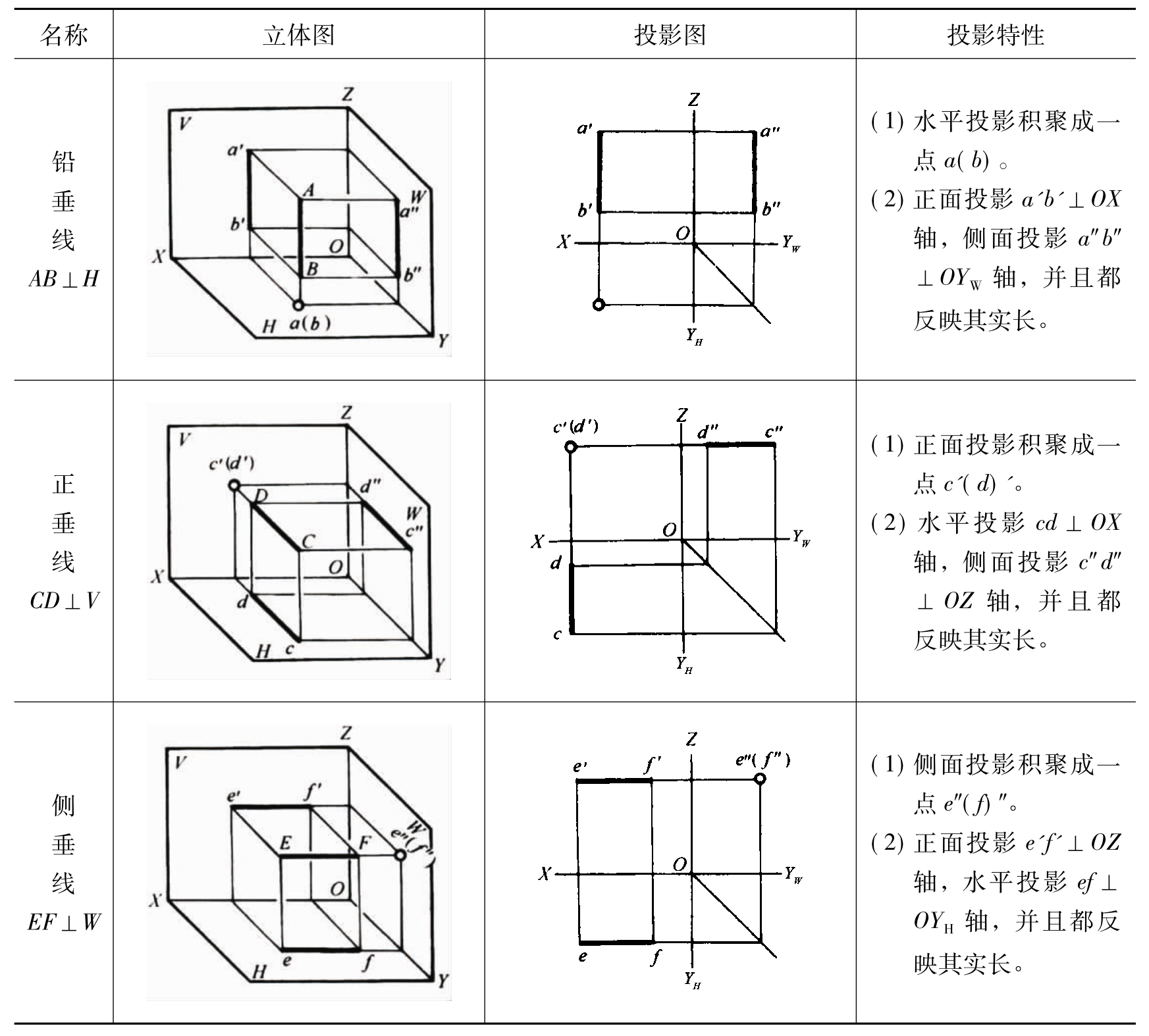
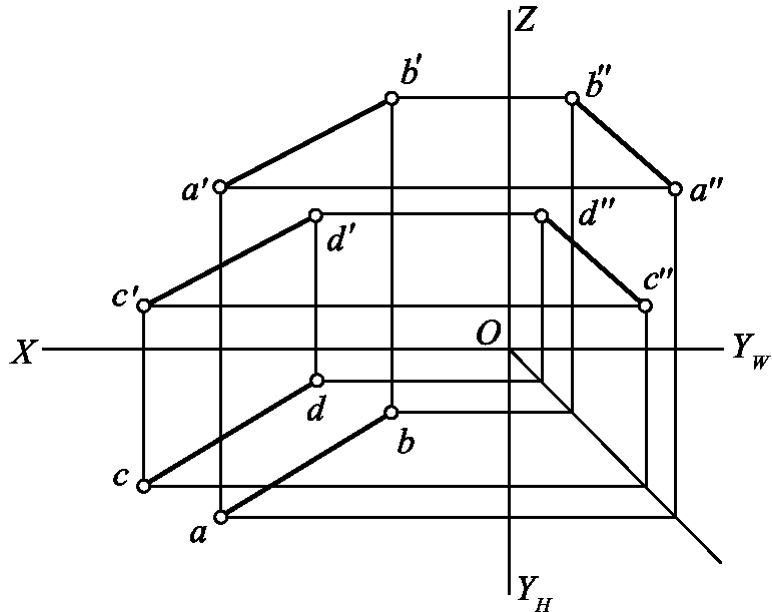
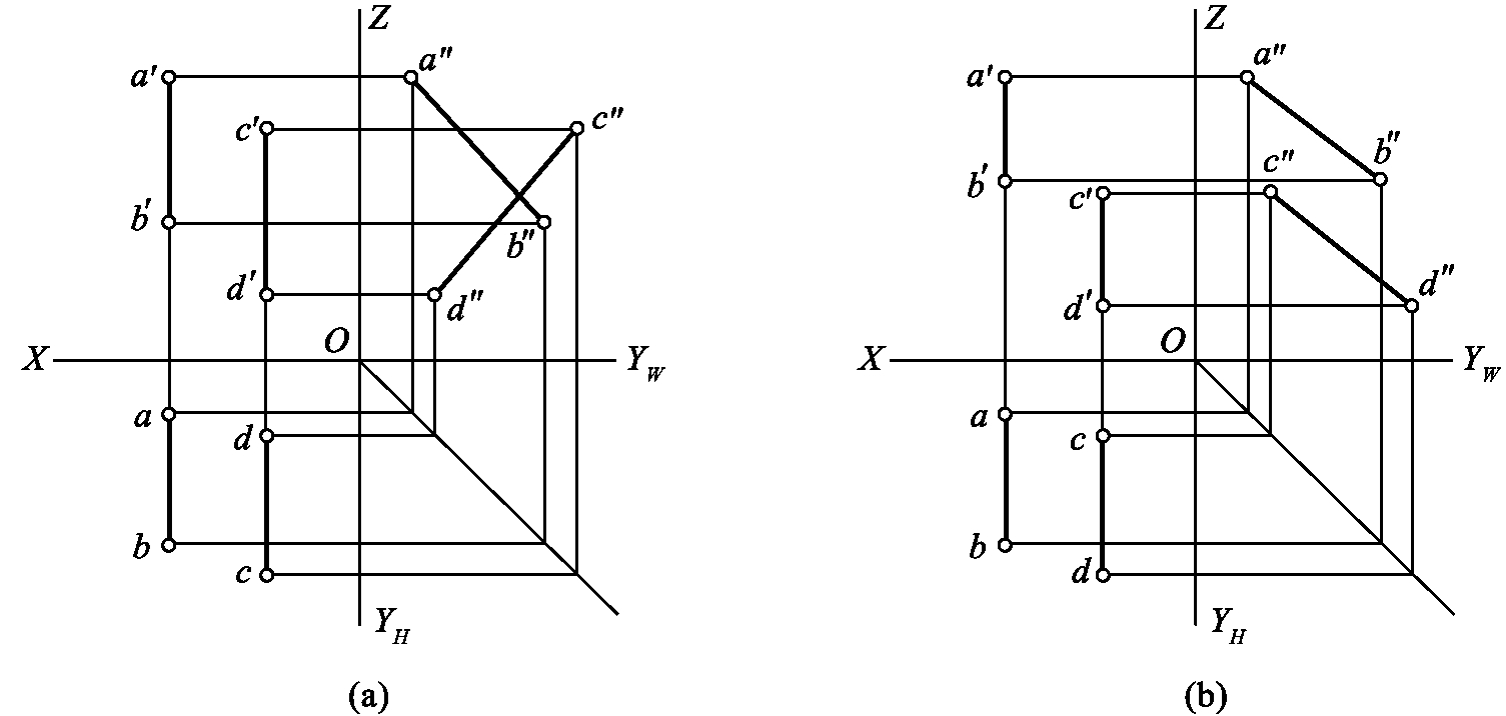
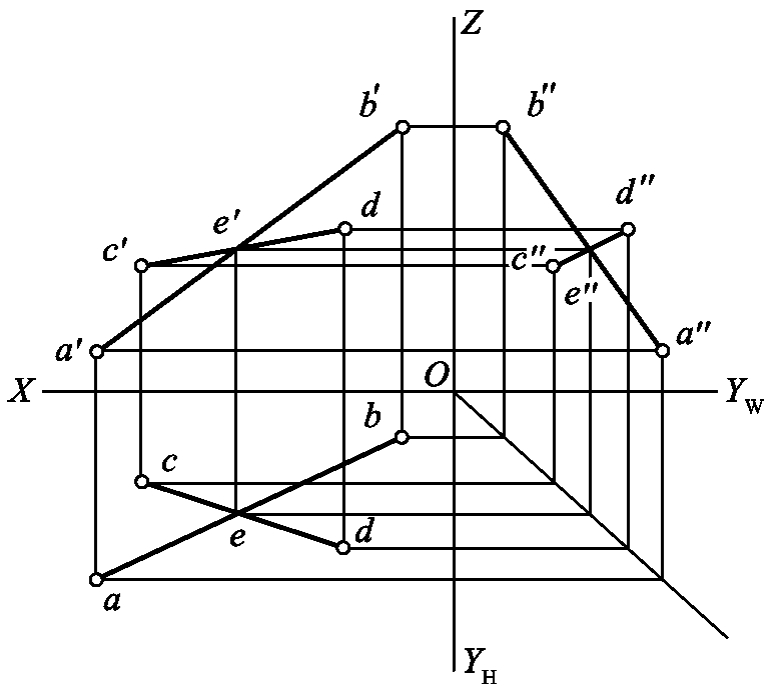
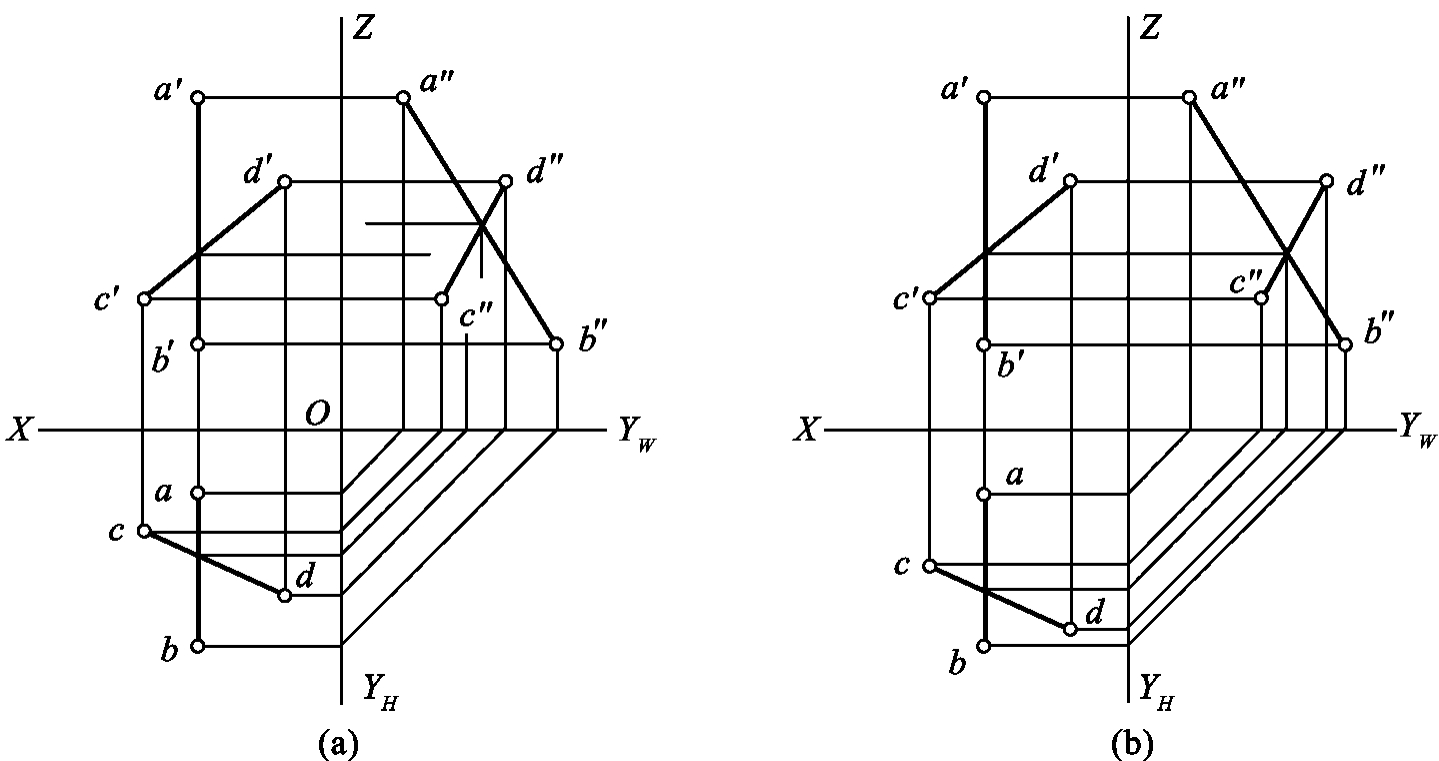
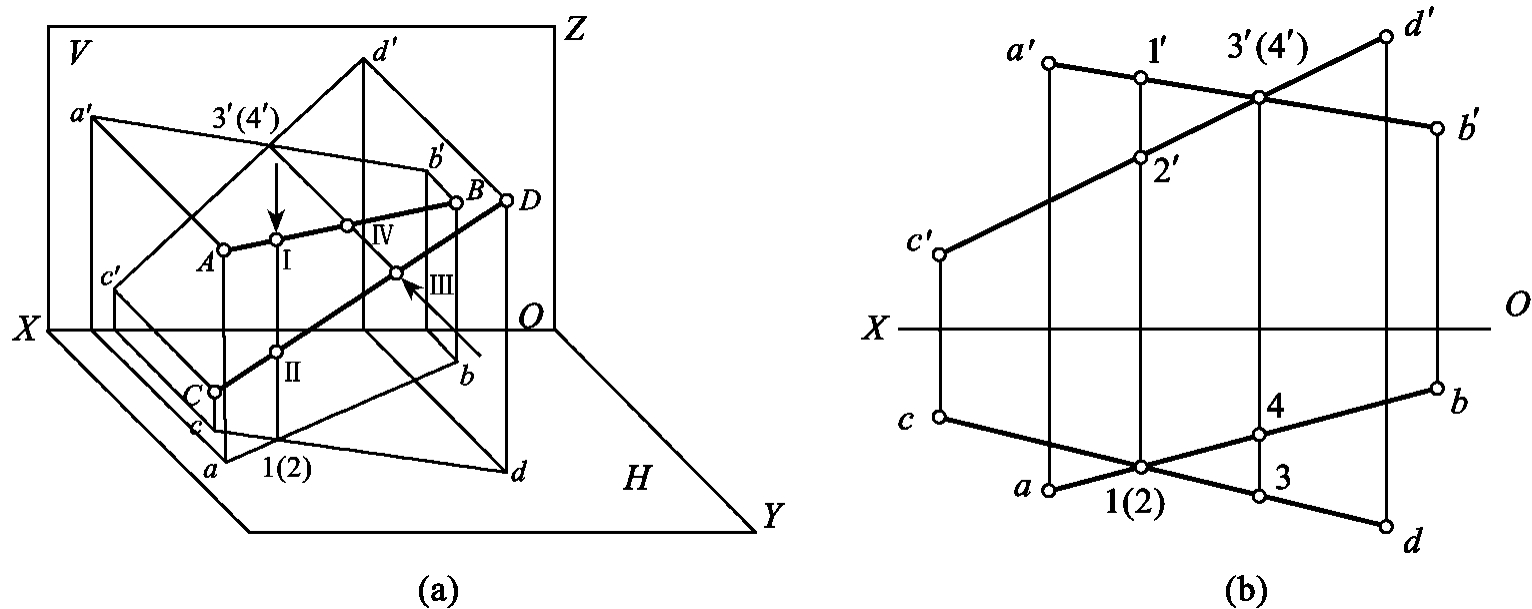
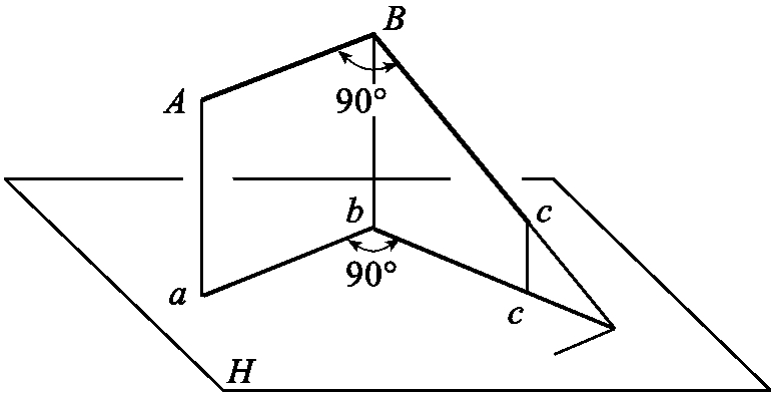
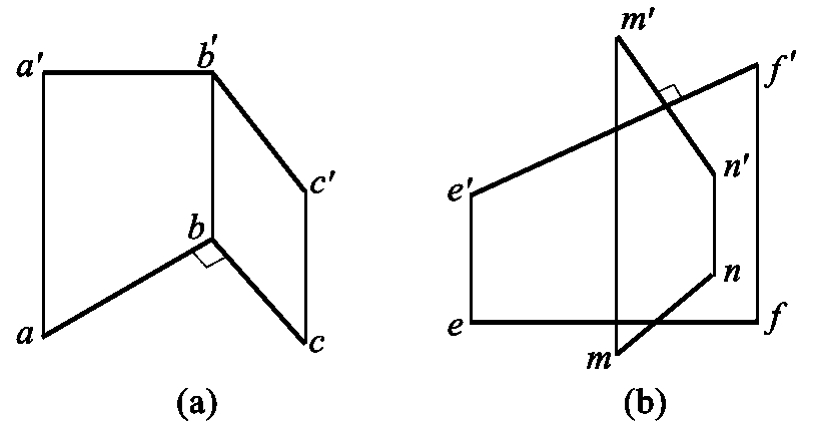
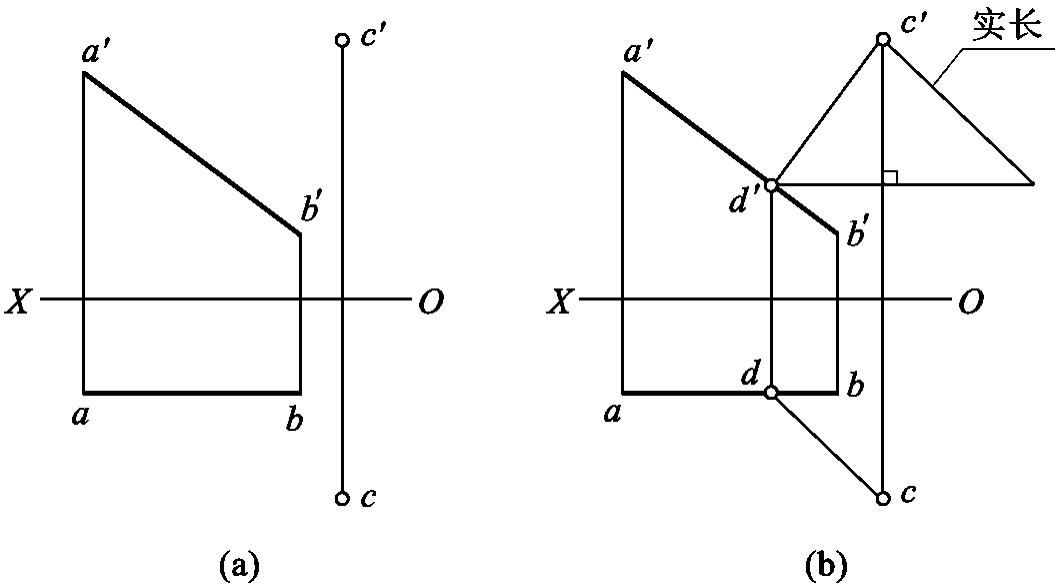
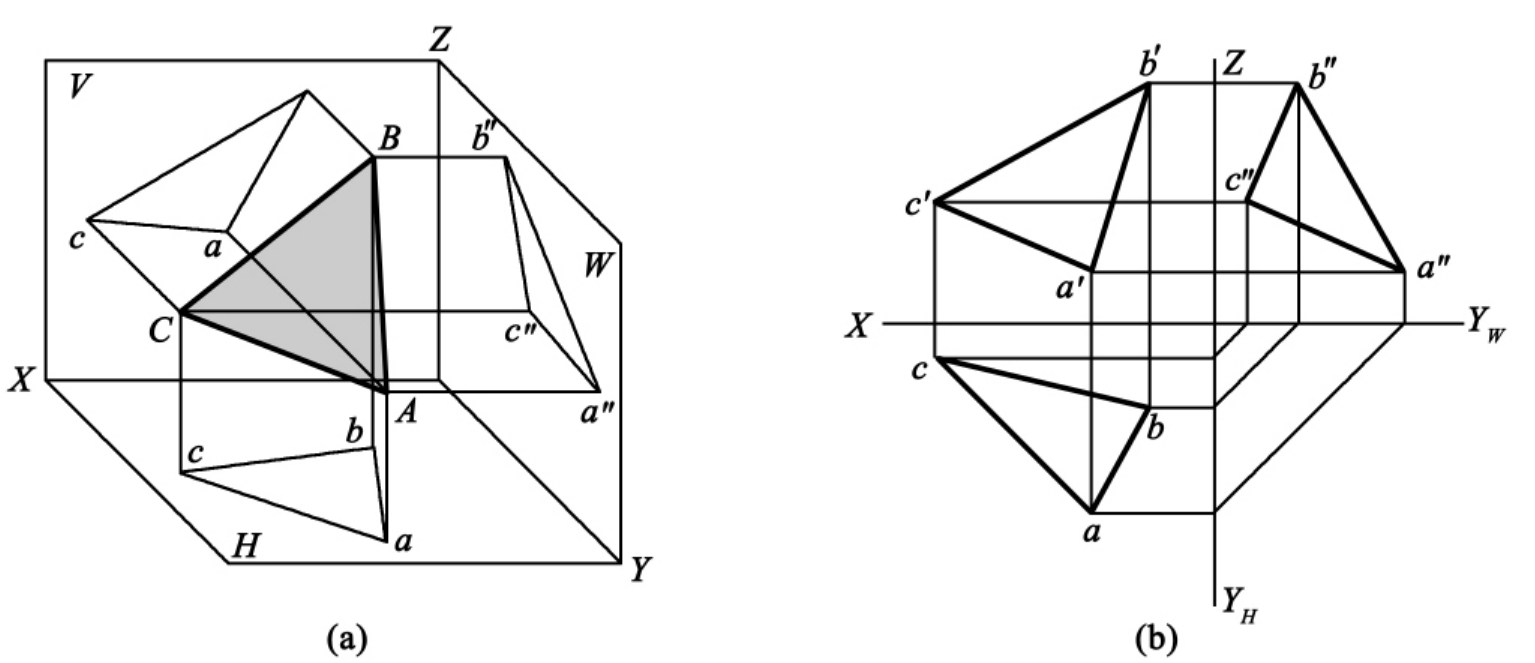
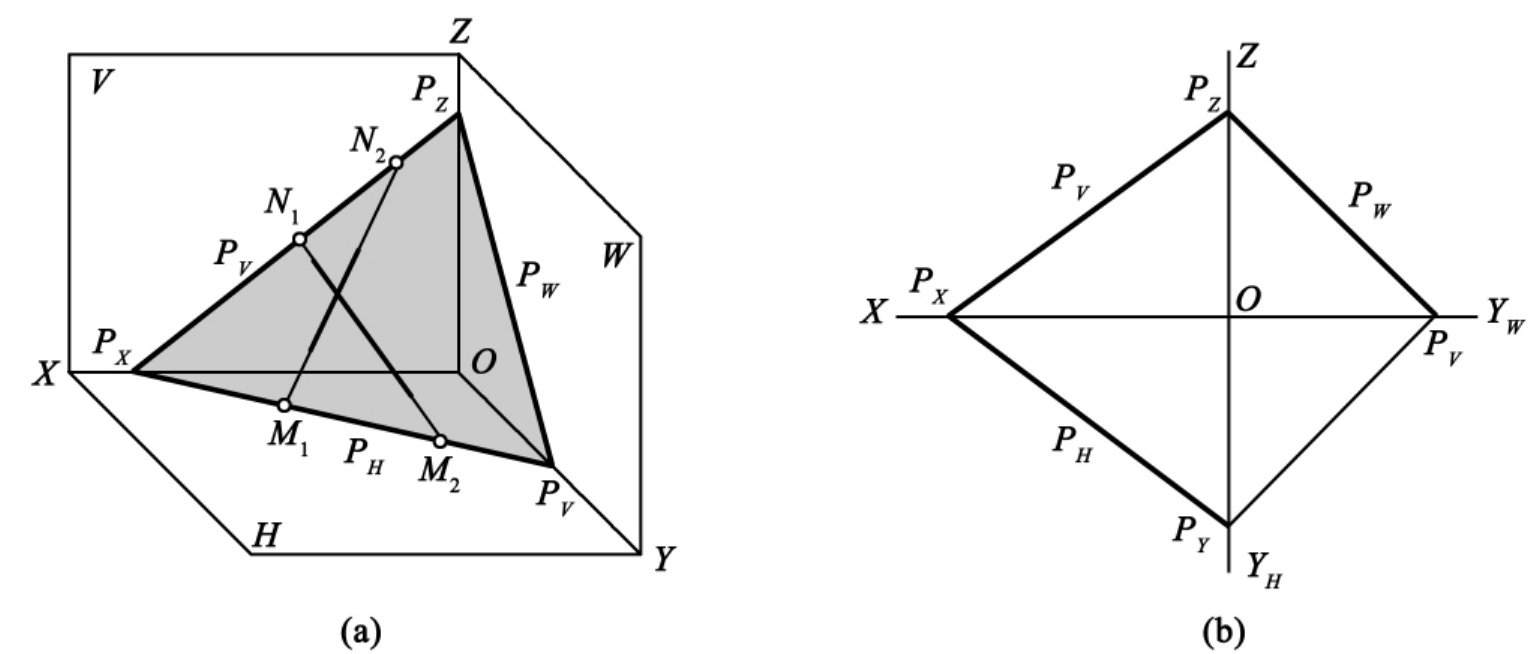
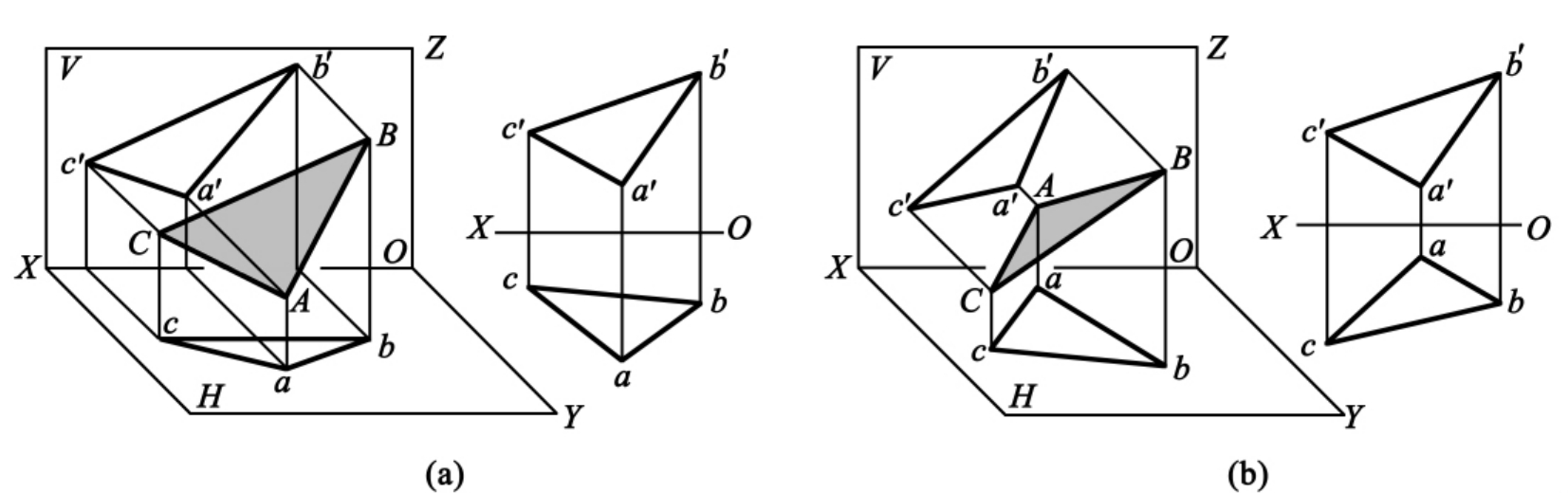
1.13.3§9.3 点、直线、平面的正投影
-
1.13.4§9.4 基本几何体的投影
-
1.13.5§9.5 组合体的正投影
-
1.13.6复习思考题9
-
1.14第10章 建筑施工图
-
1.14.1§10.1 工程制图的一般规定
-
1.14.2§10.2 建筑工程制图的基本规定
-
1.14.3§10.3 建筑总平面图
-
1.14.4§10.4 建筑平面图
-
1.14.5§10.5 建筑立面图
-
1.14.6§10.6 建筑剖面图
-
1.14.7§10.7 建筑详图
-
1.14.8复习思考题10
-
1.15第11章 景观建筑构造
-
1.15.1§11.1 景观建筑构造概述
-
1.15.2§11.2 景观道路及广场铺装
-
1.15.3§11.3 景观台阶、坡道与铺装
-
1.15.4§11.4 景观树、花池及驳岸
-
1.15.5§11.5 景观水景
-
1.15.6§11.6 景观水体驳岸
-
1.15.7§11.7 景观栏杆
-
1.15.8§11.8 景观建筑小品
-
1.15.9§11.9 景观照明
-
1.15.10复习思考题11
-
1.16参考文献
1
建筑构造与识图