-
1.1《武汉大学百年名典》出版前言
-
1.2再版说明
-
1.3序
-
1.4目录
-
1.5第一章 天体之运行
-
1.5.1第一节 实用天文学
-
1.5.2第二节 宇宙概述
-
1.5.3第三节 太阳系
-
1.5.4第四节 地 球
-
1.5.5第五节 地球之运行
-
1.6第二章 天 球
-
1.6.1第一节 天球之定义
-
1.6.2第二节 天球上之参考点圈
-
1.6.3第三节 天球上之坐标系统
-
1.6.4第四节 恒 星
-
1.6.5第五节 星座及恒星之辨认
-
1.7第三章 天体之视运动
-
1.7.1第一节 恒星之视运动
-
1.7.2第二节 太阳之视运动
-
1.7.3第三节 行星及太阴之视运动
-
1.7.4第四节 岁差及章动
-
1.7.5第五节 光行差
-
1.8第四章 时
-
1.8.1第一节 时段与时刻
-
1.8.2第二节 恒星日、恒星时
-
1.8.3第三节 太阳日、太阳时
-
1.8.4第四节 时差
-
1.8.5第五节 时与经度
-
1.8.6第六节 标准时
-
1.8.7第七节 日期界线
-
1.9第五章 天文年历
-
1.9.1第一节 天体位置
-
1.9.2第二节 年与历
-
1.9.3第三节 年历内容
-
1.9.4第四节 恒星之平位置至视位置之化算
-
1.9.5第五节 内插计算公式
-
1.10第六章 时之换算
-
1.10.1第一节 平太阳时与视太阳时之换算
-
1.10.2第二节 恒星时段与平太阳时段之关系
-
1.10.3第三节 恒星时刻与太阳时刻之关系
-
1.10.4第四节 时刻换算应用问题
-
1.10.5第五节 恒星时刻之近似估计
-
1.11第七章 定位三角形
-
1.11.1第一节 球面三角之基本公式
-
1.11.2第二节 直角或象限球面三角形
-
1.11.3第三节 定位三角形之一般解算
-
1.11.4第四节 定位三角形之特殊情形
-
1.12第八章 观测仪器
-
1.12.1第一节 经 纬 仪
-
1.12.2第二节 六 分 仪
-
1.12.3第三节 计时仪器
-
1.13第九章 高度角观测值之改正
-
1.13.1第一节 蒙 气 差
-
1.13.2第二节 视 差
-
1.13.3第三节 半 径
-
1.13.4第四节 海平俯角
-
1.13.5第五节 高度角之改正计算
-
1.14第十章 时计对正及授时信号
-
1.14.1第一节 时计改正及其日差
-
1.14.2第二节 以标准时计对正计时表
-
1.14.3第三节 无线电授时信号
-
1.14.4第四节 游标授时信号之收录
-
1.15第十一章 纬度之测定
-
1.15.1第一节 总 论
-
1.15.2第二节 天体中天高度法
-
1.15.3第三节 环子午高度法
-
1.15.4第四节 北极星高度法
-
1.15.5第五节 赫瑞鲍太尔各特法
-
1.16第十二章 时刻与经度之测定
-
1.16.1第一节 总 论
-
1.16.2第二节 天体高度法
-
1.16.3第三节 天体等高法
-
1.16.4第四节 天体中天时刻法
-
1.16.5第五节 子午仪中天观测法
-
1.16.6第六节 恒星经过北极星地平经圈时刻法
-
1.16.7第七节 经度之测定
-
1.17第十三章 同时测定经纬度方法
-
1.17.1第一节 测两星高度定经纬度
-
1.17.2第二节 定位线解法
-
1.17.3第三节 定位线公式
-
1.17.4第四节 等高观测原理
-
1.17.5第五节 等 高 仪
-
1.17.6第六节 等高仪观测之选星
-
1.17.7第七节 等高仪之观测工作
-
1.17.8第八节 等高仪观测计算举例
-
1.18第十四章 方位角之测定
-
1.18.1第一节 方位角及方位标
-
1.18.2第二节 测定方位角一般原理
-
1.18.3第三节 天体高度法
-
1.18.4第四节 太阳时角法
-
1.18.5第五节 拱极星在大距法
-
1.18.6第六节 拱极星近大距法
-
1.18.7第七节 近极星任意时角法
-
1.18.8第八节 太阳仪附件法
-
1.18.9第九节 子午线收敛角
-
1.19附 表
-
1.20索 引
1
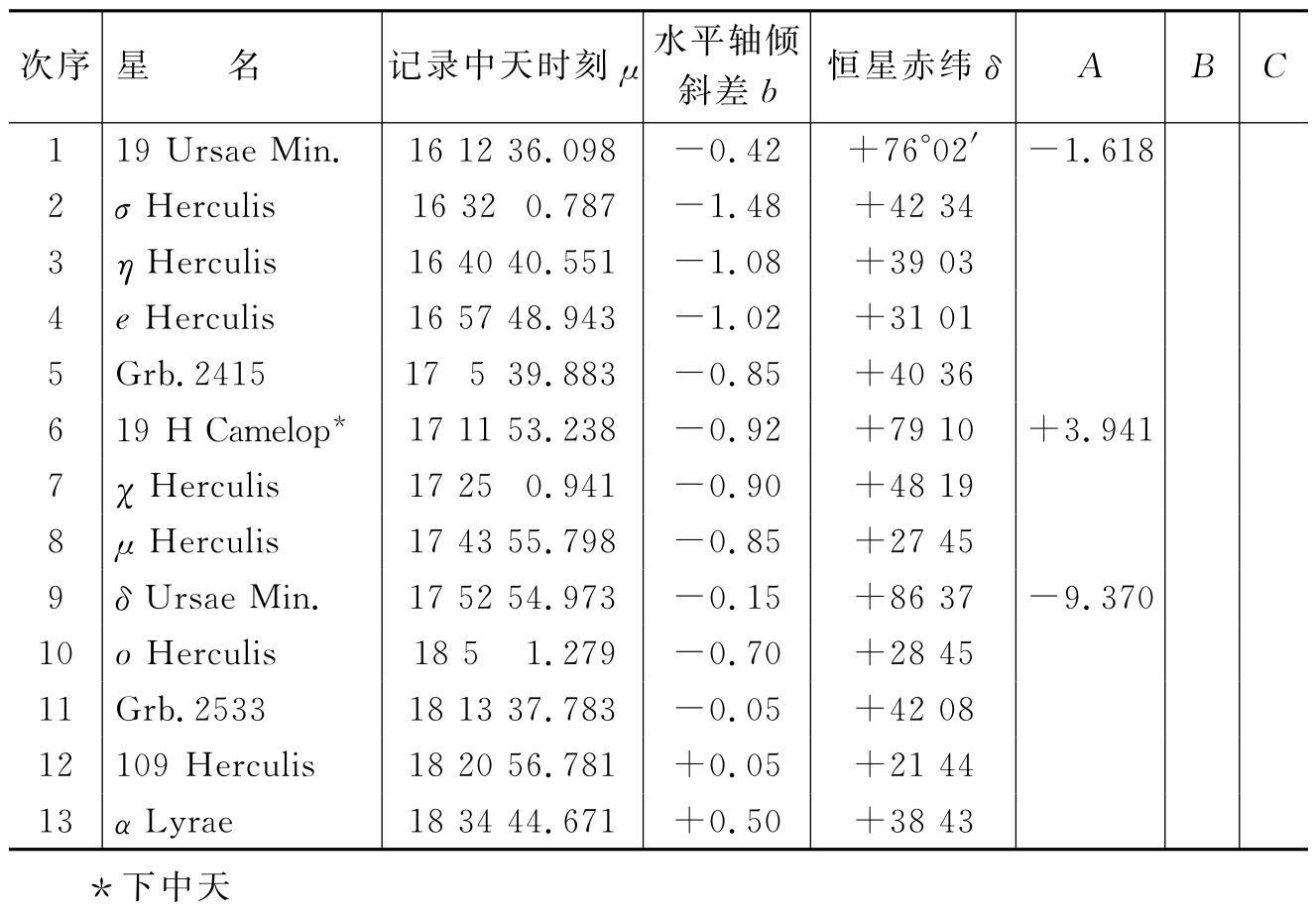
实用天文学

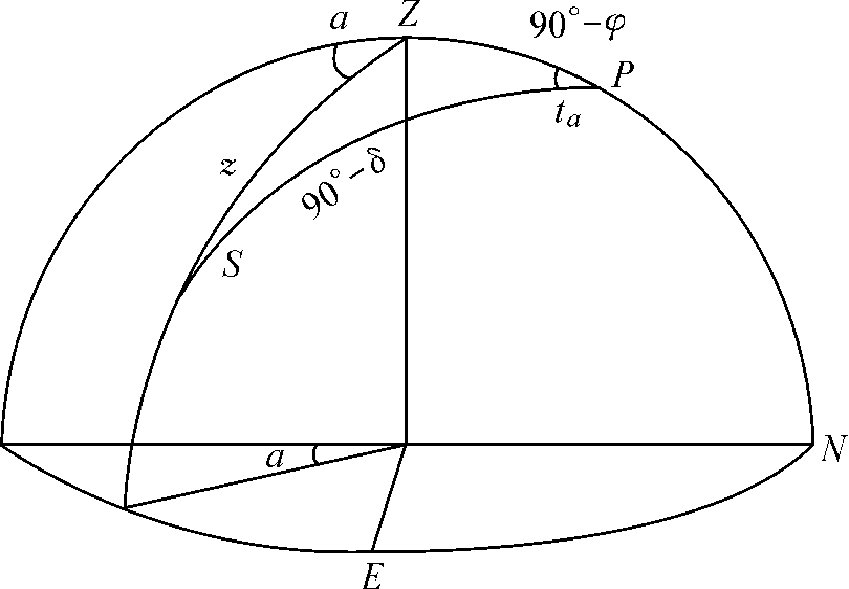
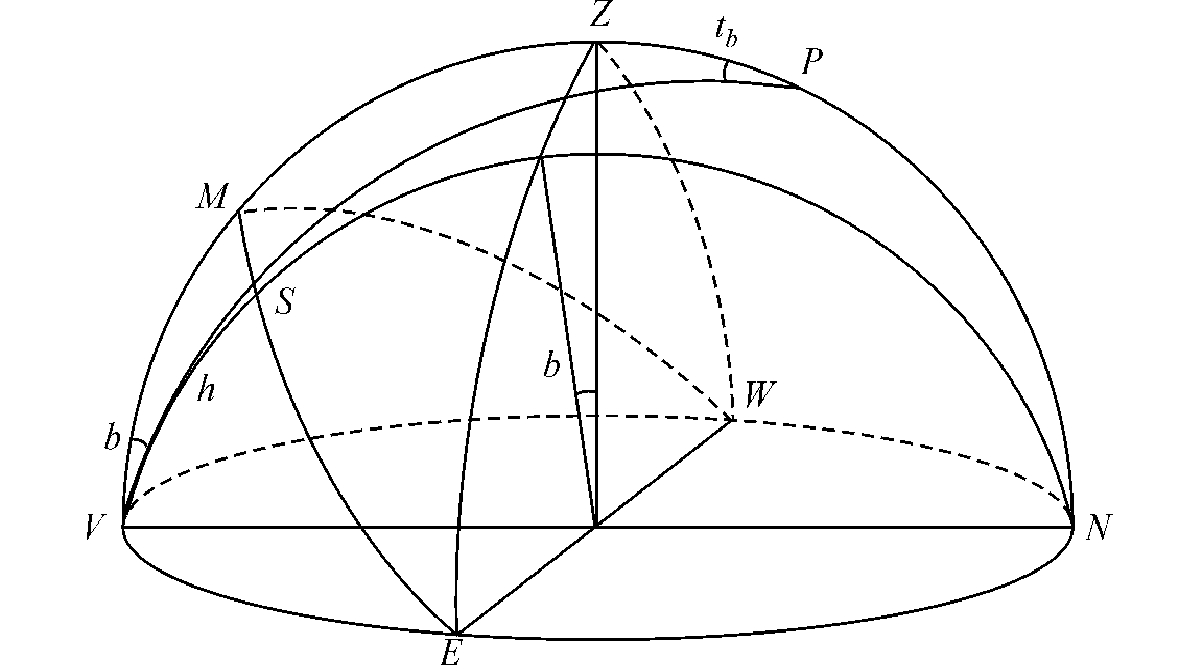
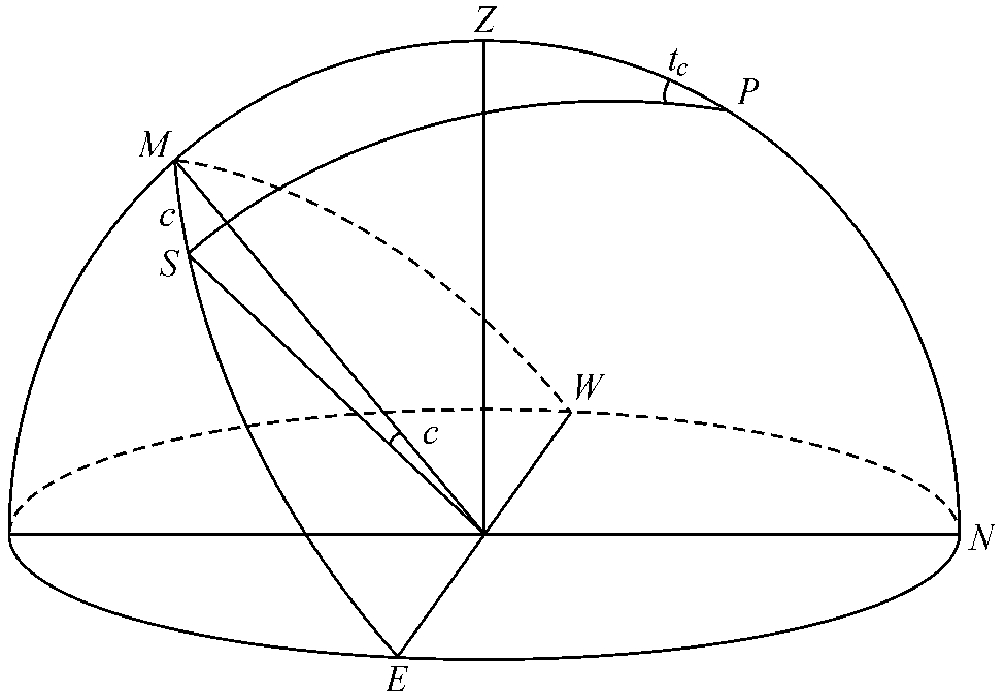
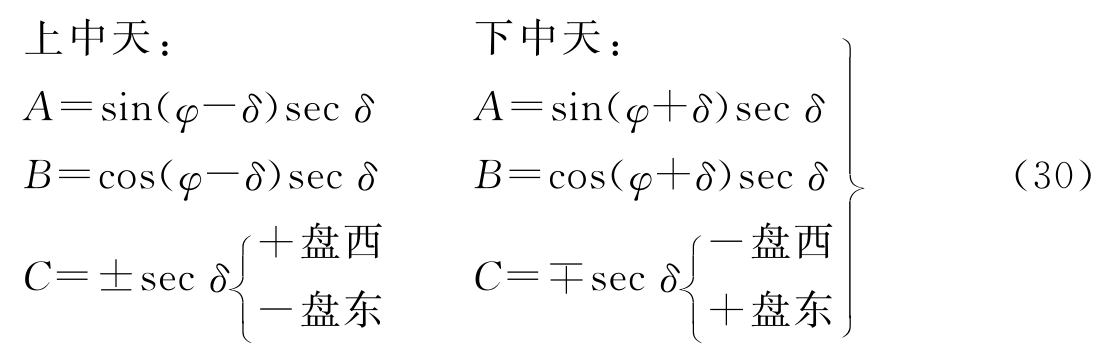
 。此误差与前述之视准轴差相同,故对于观测时刻之影响为
。此误差与前述之视准轴差相同,故对于观测时刻之影响为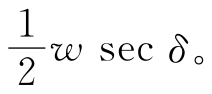 与白金条宽改正同时尚有测微器螺旋之齿隙改正,设齿隙为l,以时秒计,其改正遂为
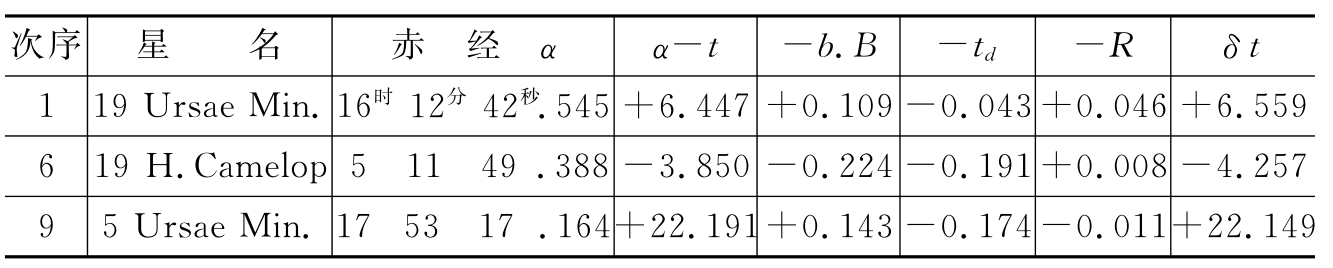
与白金条宽改正同时尚有测微器螺旋之齿隙改正,设齿隙为l,以时秒计,其改正遂为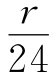 =+0秒.032,根据式(33)以t0=17时24分.0为准,可计算日差改正R。
=+0秒.032,根据式(33)以t0=17时24分.0为准,可计算日差改正R。