-
1.1第一章 导论:公共政策与公共政策学
-
1.1.1第一节 公共政策概说
-
1.1.1.1一、公共政策的内涵
-
1.1.1.2二、政策制定与行政决策的区别和联系
-
1.1.1.3三、公共政策的基本特征
-
1.1.1.4四、公共政策的类型
-
1.1.1.5五、公共政策的功能
-
1.1.2第二节 公共政策学的形成与发展
-
1.1.2.1一、什么是公共政策学
-
1.1.2.2二、公共政策学的形成与发展
-
1.1.2.3三、当代中国的公共政策学
-
1.2第二章 政策研究组织与政策模型
-
1.2.1第一节 政策研究组织的类型及其历史发展
-
1.2.1.1一、什么是政策研究组织
-
1.2.1.2二、政策研究组织的类型
-
1.2.1.3三、政策研究组织的历史发展
-
1.2.2第二节 代表性的政策模型
-
1.2.2.1一、精英决策模型
-
1.2.2.2二、集团决策模型
-
1.2.2.3三、政治系统决策模型
-
1.2.2.4四、完全理性决策模型
-
1.2.2.5五、有限理性决策模型
-
1.2.2.6六、非理性决策模型
-
1.2.2.7七、渐进决策模型
-
1.2.2.8八、混合扫描决策模型
-
1.3第三章 政策环境
-
1.3.1第一节 政策环境概述
-
1.3.1.1一、政策环境的含义
-
1.3.1.2二、公共政策与政策环境的互动
-
1.3.1.3三、政策环境的特征
-
1.3.2第二节 自然环境
-
1.3.2.1一、自然环境与公共政策
-
1.3.2.2二、自然环境的构成
-
1.3.3第三节 经济与社会环境
-
1.3.3.1一、经济环境
-
1.3.3.2二、社会环境
-
1.3.4第四节 政治与文化环境
-
1.3.4.1一、政治环境
-
1.3.4.2二、文化环境
-
1.3.5第五节 国际环境
-
1.3.5.1一、全球化:国内与国际的互动
-
1.3.5.2二、和平与发展的世界
-
1.3.5.3三、全球问题与全球治理
-
1.4第四章 政策问题与政策议程
-
1.4.1第一节 政策问题的确认
-
1.4.1.1一、问题与政策问题
-
1.4.1.2二、政策问题的特征
-
1.4.1.3三、政策问题的类型
-
1.4.1.4四、政策问题确认的一般程序
-
1.4.2第二节 政策议程的构建
-
1.4.2.1一、政策议程的界定及其类型
-
1.4.2.2二、影响政策议程的行为者
-
1.4.2.3三、构建政策议程的时机
-
1.4.2.4四、政策议程的构建模型
-
1.5第五章 政策规划
-
1.5.1第一节 政策规划和政策规划者
-
1.5.1.1一、政策规划的含义
-
1.5.1.2二、政策规划的原则
-
1.5.1.3三、政策规划的分类
-
1.5.1.4四、政策规划者的概念
-
1.5.1.5五、政策规划者应注意的问题
-
1.5.2第二节 政策规划的主要步骤
-
1.5.2.1一、目标确定
-
1.5.2.2二、方案设计
-
1.5.2.3三、方案审议
-
1.5.2.4四、方案择优
-
1.6第六章 政策采纳与政策合法化
-
1.6.1第一节 政策采纳
-
1.6.1.1一、政策采纳的概念
-
1.6.1.2二、政策采纳的重要性
-
1.6.1.3三、影响政策采纳的因素
-
1.6.1.4四、政策采纳的原则
-
1.6.2第二节 政策合法化
-
1.6.2.1一、合法性的界定
-
1.6.2.2二、合法性的基础
-
1.6.2.3三、政策合法化的含义
-
1.6.2.4四、政策合法化与政策法律化
-
1.6.2.5五、政策合法化的主体与程序
-
1.7第七章 政策执行
-
1.7.1第一节 政策执行概说
-
1.7.1.1一、政策执行的含义
-
1.7.1.2二、政策执行的重要性
-
1.7.1.3三、政策执行研究的兴起
-
1.7.1.4四、政策执行应遵循的原则
-
1.7.1.5五、政策工具
-
1.7.2第二节 政策执行模型
-
1.7.2.1一、史密斯的过程模型
-
1.7.2.2二、麦克拉夫林的调适模型
-
1.7.2.3三、霍恩和米特的系统模型
-
1.7.2.4四、萨巴蒂尔和梅兹曼尼安的综合模型
-
1.7.3第三节 影响政策执行的主要因素
-
1.7.3.1一、政策决定
-
1.7.3.2二、政策执行者
-
1.7.3.3三、政策目标群体
-
1.7.3.4四、政策环境
-
1.7.4第四节 “上有政策,下有对策”
-
1.7.4.1一、“上有政策,下有对策”的表现
-
1.7.4.2二、“上有政策,下有对策”的成因
-
1.7.4.3三、“上有政策,下有对策”的治理
-
1.8第八章 政策评估
-
1.8.1第一节 政策评估的概念及类型
-
1.8.1.1一、政策评估的概念
-
1.8.1.2二、政策评估的意义
-
1.8.1.3三、政策评估的兴起及其发展
-
1.8.1.4四、政策评估的类型
-
1.8.2第二节 政策评估的实施
-
1.8.2.1一、政策评估的标准
-
1.8.2.2二、政策评估的步骤
-
1.8.2.3三、政策评估的方法
-
1.8.2.4四、政策评估的障碍
-
1.9第九章 政策调整与政策终结
-
1.9.1第一节 政策调整
-
1.9.1.1一、政策调整的含义和作用
-
1.9.1.2二、政策调整的原则和形式
-
1.9.1.3三、政策调整中应注意的问题
-
1.9.2第二节 政策终结
-
1.9.2.1一、政策终结的内涵
-
1.9.2.2二、政策终结的倡导者
-
1.9.2.3三、政策终结的对象
-
1.9.2.4四、政策终结的方式
-
1.9.2.5五、政策终结的障碍和应对措施
-
1.10第十章 政策分析方法初步
-
1.10.1第一节 政策分析方法概述
-
1.10.1.1一、政策分析的含义
-
1.10.1.2二、政策分析人员及其素质
-
1.10.1.3三、政策分析的类型
-
1.10.1.4四、政策分析与系统分析
-
1.10.2第二节 政策分析的定性方法
-
1.10.2.1一、价值分析
-
1.10.2.2二、头脑风暴法
-
1.10.2.3三、德尔菲法
-
1.10.3第三节 政策分析的定量方法
-
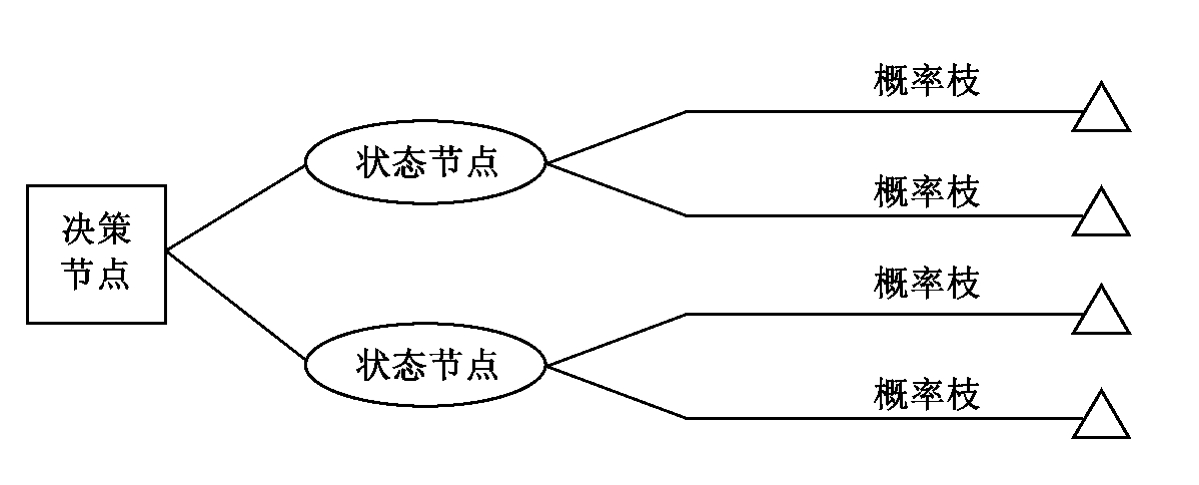
1.10.3.1一、决策树分析
-
1.10.3.2二、成本收益分析
-
1.10.3.3三、回归分析
-
1.11参考文献
-
1.12后 记
1
公共政策学