-
1.1前 言
-
1.2第1章 移动通信概述
-
1.2.11.1 引 言
-
1.2.21.2 移动通信的分类
-
1.2.31.3 移动通信的发展
-
1.2.3.11.3.1 第一代——模拟蜂窝通信系统
-
1.2.3.21.3.2 第二代——数字蜂窝移动通信系统
-
1.2.3.31.3.3 第三代——IMT-2000
-
1.2.3.41.3.4 第四代移动通信系统
-
1.2.41.4 移动通信的构成和特点
-
1.2.4.11.4.1 蜂窝移动电话系统构成
-
1.2.4.21.4.2 移动通信的特点
-
1.2.51.5 移动通信的工作方式
-
1.2.61.6 移动通信的频率分配
-
1.2.71.7 移动通信中的基本技术
-
1.2.7.11.7.1 移动通信网的组网技术
-
1.2.7.21.7.2 编码技术
-
1.2.7.31.7.3 数字调制
-
1.2.7.41.7.4 抗衰落技术
-
1.2.7.51.7.5 移动交换技术
-
1.2.8习题与思考题
-
1.3第2章 GSM 和GPBS通信系统
-
1.3.12.1 概 述
-
1.3.1.12.1.1 GSM系统发展过程
-
1.3.1.22.1.2 GSM系统的基本特点
-
1.3.1.32.1.3 主要技术及参数
-
1.3.22.2 GSM系统组成
-
1.3.2.12.2.1 GSM系统的结构与功能
-
1.3.2.22.2.2 GSM系统的接口和协议
-
1.3.2.32.2.3 GSM网络结构
-
1.3.32.3 GSM系统的编号
-
1.3.3.12.3.1 无线覆盖的区域划分
-
1.3.3.22.3.2 移动识别号码
-
1.3.42.4 GSM系统的无线接口
-
1.3.4.12.4.1 GSM的频率配置
-
1.3.4.22.4.2 多址方式
-
1.3.4.32.4.3 GSM的无线数字传输技术
-
1.3.52.5 GSM系统的控制和管理
-
1.3.5.12.5.1 GSM系统的控制过程
-
1.3.5.22.5.2 GSM系统的安全性管理
-
1.3.5.32.5.3 GSM系统移动性管理
-
1.3.62.6 通用分组无线业务
-
1.3.6.12.6.1 概述
-
1.3.6.22.6.2 GPRS的特点及主要业务
-
1.3.6.32.6.3 GPRS网络结构
-
1.3.6.42.6.4 GPRS的移动性管理
-
1.3.6.52.6.5 GPRS的会话管理
-
1.3.6.62.6.6 业务流程举例
-
1.3.7习题与思考题
-
1.4第3章 码分多址技术基础
-
1.4.13.1 概 述
-
1.4.1.13.1.1 CDMA技术的产生与发展
-
1.4.1.23.1.2 CDMA技术的优势
-
1.4.23.2 码分多址的基本原理
-
1.4.33.3 扩频通信系统
-
1.4.3.13.3.1 扩频通信的基本概念
-
1.4.3.23.3.2 扩频通信的性能指标
-
1.4.3.33.3.3 扩频通信的实现方法
-
1.4.43.4 CDMA的地址码和扩频码
-
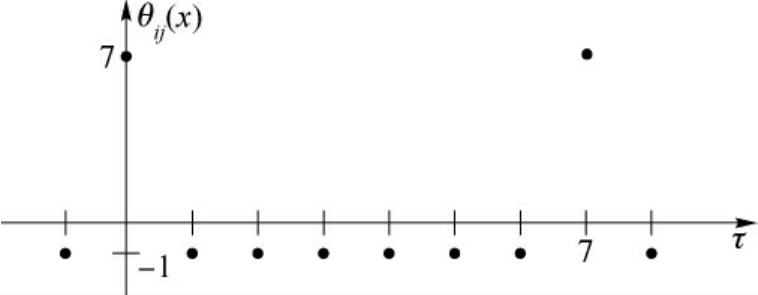
1.4.4.13.4.1 相关函数
-
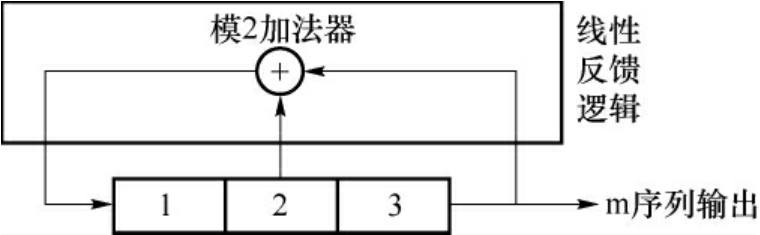
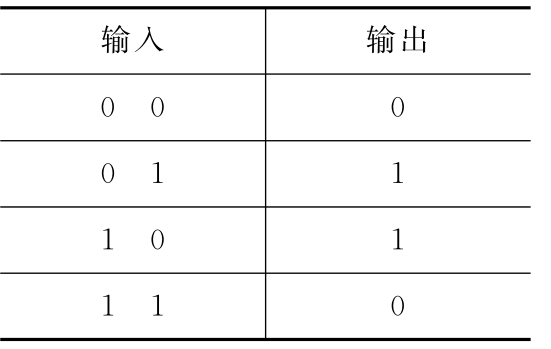
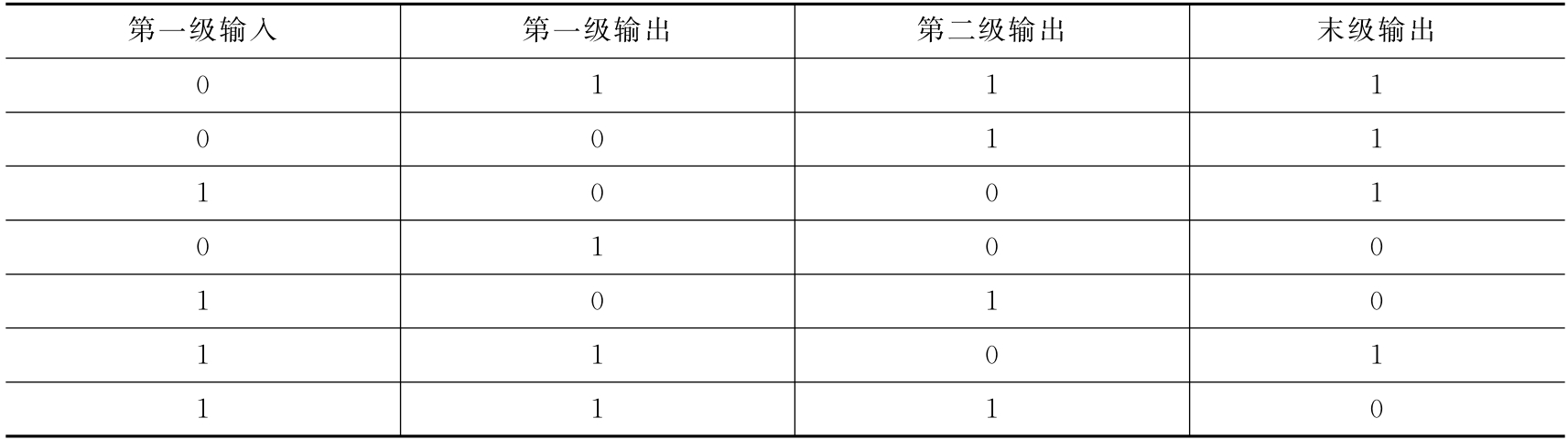
1.4.4.23.4.2 PN码
-
1.4.4.33.4.3 Walsh码
-
1.4.4.43.4.4 PN码与Walsh码在N-CDMA移动通信中的应用
-
1.4.53.5 CDMA技术的特点
-
1.4.5.13.5.1 CDMA技术的优点
-
1.4.5.23.5.2 CDMA技术实施中出现的问题
-
1.4.6习题与思考题
-
1.5第4章 IS-95 CDMA和CDMA2000 1x系统
-
1.5.14.1 概 述
-
1.5.24.2 IS-95CDMA的网络结构
-
1.5.2.14.2.1 IS-95CDMA系统的网络参考模型
-
1.5.2.24.2.2 IS-95CDMA的网络结构
-
1.5.34.3 蜂窝小区构成及频率配置
-
1.5.3.14.3.1 蜂窝小区构成
-
1.5.3.24.3.2 频率配置
-
1.5.44.4 IS-95CDMA的信道划分
-
1.5.4.14.4.1 前向链路信道结构
-
1.5.4.24.4.2 反向链路信道结构
-
1.5.54.5 IS-95CDMA的功率控制技术
-
1.5.64.6 IS-95CDMA的软切换技术
-
1.5.74.7 CDMA2000 1x系统
-
1.5.7.14.7.1 概述
-
1.5.7.24.7.2 CDMA2000 1x的体系结构
-
1.5.7.34.7.3 CDMA2000 1x的空中接口概述
-
1.5.7.44.7.4 CDMA2000 1x的空中接口的物理层
-
1.5.7.54.7.5 CDMA2000 1x的功率控制和系统切换
-
1.5.7.64.7.6 CDMA2000 1x业务体系
-
1.5.8习题与思考题
-
1.6第5章 第三代移动通信系统
-
1.6.15.1 概 述
-
1.6.1.15.1.1 第三代移动通信系统的目标和要求
-
1.6.1.25.1.2 3G标准化组织
-
1.6.1.35.1.3 2G系统向3G的演进策略
-
1.6.1.45.1.4 3G的三种主流技术
-
1.6.1.55.1.5 3G系统结构
-
1.6.1.65.1.6 3G频谱情况
-
1.6.1.75.1.7 3G系统的业务
-
1.6.25.2 WCDMA
-
1.6.2.15.2.1 WCDMA标准历程
-
1.6.2.25.2.2 WCDMA空中接口协议
-
1.6.2.35.2.3 WCDMA空中接口三层信道
-
1.6.2.45.2.4 WCDMA无线接口关键技术
-
1.6.2.55.2.5 高速下行分组接入技术
-
1.6.2.65.2.6 高速上行分组接入技术
-
1.6.35.3 TD-SCDMA
-
1.6.3.15.3.1 TD-SCDMA标准历程
-
1.6.3.25.3.2 TD-SCDMA网络结构
-
1.6.3.35.3.3 TD-SCDMA空中接口物理层
-
1.6.3.45.3.4 TD-SCDMA关键技术
-
1.6.45.4 CDMA2000
-
1.6.4.15.4.1 CDMA2000标准历程
-
1.6.4.25.4.2 CDMA2000 1xEV-DO概述
-
1.6.4.35.4.3 CDMA2000 1xEV-DO Rev A物理信道的结构
-
1.6.4.45.4.4 CDMA2000 1xEV-DO Rev A的关键技术
-
1.6.55.5 WiMAX
-
1.6.6习题与思考题
-
1.6.7参考文献
1
移动通信原理与系统