-
1.1全国高等院校环境科学与工程统编教材编写指导委员会
-
1.2内容提要
-
1.3前 言
-
1.4第1章 绪 论
-
1.4.11.1 环境问题的产生
-
1.4.1.11.1.1 环境与环境问题
-
1.4.1.21.1.2 环境问题的产生
-
1.4.1.31.1.3 全球性环境问题及危害
-
1.4.21.2 环境生态学的产生及发展趋势
-
1.4.2.11.2.1 环境生态学的定义
-
1.4.2.21.2.2 环境生态学的产生
-
1.4.2.31.2.3 环境生态学的研究内容及其发展趋势
-
1.4.31.3 环境生态学与生态学及相邻学科的关系
-
1.4.3.11.3.1 生态学
-
1.4.3.21.3.2 环境科学
-
1.4.3.31.3.3 其他相关学科
-
1.4.4思考与练习题
-
1.5第2章 生物与环境
-
1.5.12.1 环境因子与生态因子
-
1.5.1.12.1.1 环境与环境因子
-
1.5.1.22.1.2 生态因子
-
1.5.1.32.1.3 生态因子的类型
-
1.5.22.2 生物与环境的关系
-
1.5.2.12.2.1 生态因子作用的一般特征
-
1.5.2.22.2.2 生物对生态因子的耐受限度
-
1.5.2.32.2.3 生命系统的稳态特性
-
1.5.2.42.2.4 生物对环境的适应
-
1.5.32.3 生态因子的作用及生物的适应
-
1.5.3.12.3.1 光的生态作用与生物的适应
-
1.5.3.22.3.2 温度的生态作用与生物的适应
-
1.5.3.32.3.3 水的生态作用与生物的适应
-
1.5.3.42.3.4 土壤因子的生态作用与生物的适应
-
1.5.3.52.3.5 风对生物的影响
-
1.5.3.62.3.6 生物因子对生物的影响
-
1.5.4思考与练习题
-
1.6第3章 种群生态学
-
1.6.13.1 种群的概念和基本特征
-
1.6.1.13.1.1 种群的概念
-
1.6.1.23.1.2 种群的基本特征
-
1.6.23.2 种群的动态
-
1.6.2.13.2.1 种群的统计特征
-
1.6.2.23.2.2 种群增长模型
-
1.6.2.33.2.3 种群的空间分布格局
-
1.6.2.43.2.4 自然种群的数量变动
-
1.6.2.53.2.5 种群的调节
-
1.6.2.63.2.6 种群适应对策
-
1.6.33.3 种群关系
-
1.6.3.13.3.1 种内关系
-
1.6.3.23.3.2 种间关系
-
1.6.4思考与练习题
-
1.7第4章 群落生态学
-
1.7.14.1 生物群落的概念和基本特征
-
1.7.1.14.1.1 生物群落的概念及其研究内容
-
1.7.1.24.1.2 群落的基本特征
-
1.7.24.2 群落的组成
-
1.7.2.14.2.1 群落组成的性质分析
-
1.7.2.24.2.2 群落物种组成的数量特征
-
1.7.2.34.2.3 种间关联
-
1.7.34.3 群落的结构
-
1.7.3.14.3.1 群落的结构要素
-
1.7.3.24.3.2 群落的垂直结构
-
1.7.3.34.3.3 群落的水平格局
-
1.7.3.44.3.4 群落的时间格局
-
1.7.3.54.3.5 群落的交错区和边缘效应
-
1.7.3.64.3.6 影响群落组成和结构的因素
-
1.7.44.4 群落的演替
-
1.7.4.14.4.1 群落演替的概念
-
1.7.4.24.4.2 群落的形成及发育
-
1.7.4.34.4.3 群落演替的类型
-
1.7.4.44.4.4 群落演替的理论
-
1.7.4.54.4.5 有机体论和个体论的两种演替观
-
1.7.5思考与练习题
-
1.8第5章 生态系统生态学
-
1.8.15.1 生态系统的概念及基本特征
-
1.8.1.15.1.1 生态系统的概念
-
1.8.1.25.1.2 生态系统概念的发展
-
1.8.1.35.1.3 生态系统的基本特征
-
1.8.25.2 生态系统的组成与结构
-
1.8.2.15.2.1 生态系统的组成成分
-
1.8.2.25.2.2 生态系统的结构
-
1.8.35.3 生态系统的物质生产
-
1.8.3.15.3.1 初级生产
-
1.8.3.25.3.2 次级生产
-
1.8.45.4 生态系统的能量流动
-
1.8.4.15.4.1 生态系统能量传递的热力学定律
-
1.8.4.25.4.2 能量在生态系统中的流动
-
1.8.4.35.4.3 能量在生态系统中流动的特点
-
1.8.4.45.4.4 生态系统中的物质分解与能量循环
-
1.8.55.5 生态系统的物质循环
-
1.8.5.15.5.1 物质循环的概念及特点
-
1.8.5.25.5.2 水循环
-
1.8.5.35.5.3 碳循环
-
1.8.5.45.5.4 氮循环
-
1.8.5.55.5.5 磷循环
-
1.8.5.65.5.6 硫循环
-
1.8.5.75.5.7 有毒有害物质的循环
-
1.8.65.6 生态系统的信息传递
-
1.8.6.15.6.1 信息与信息量
-
1.8.6.25.6.2 信息及其传递
-
1.8.75.7 生态系统的平衡及自我调节
-
1.8.7.15.7.1 生态平衡的概念
-
1.8.7.25.7.2 生态平衡的调节机制
-
1.8.85.8 生物圈主要生态系统
-
1.8.8.15.8.1 森林生态系统
-
1.8.8.25.8.2 草原生态系统
-
1.8.8.35.8.3 河流生态系统
-
1.8.8.45.8.4 湖泊生态系统
-
1.8.8.55.8.5 湿地生态系统
-
1.8.8.65.8.6 海洋生态系统
-
1.8.8.75.8.7 城市生态系统
-
1.8.9思考与练习题
-
1.9第6章 景观生态学与全球生态学
-
1.9.16.1 景观生态学
-
1.9.1.16.1.1 景观和景观生态学
-
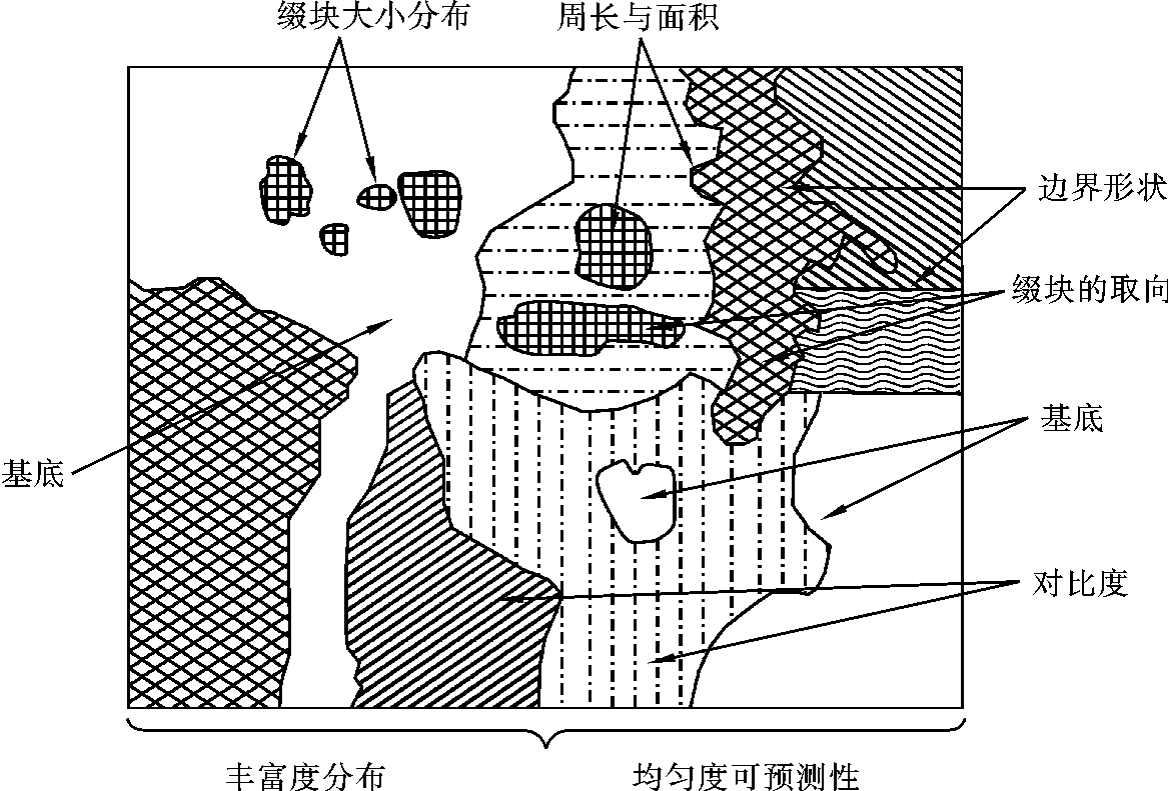
1.9.1.26.1.2 景观结构
-
1.9.1.36.1.3 景观生态过程
-
1.9.1.46.1.4 景观动态变化
-
1.9.1.56.1.5 景观生态学的研究方法
-
1.9.1.66.1.6 景观生态学的应用
-
1.9.26.2 全球变化与全球生态学
-
1.9.2.16.2.1 全球变化
-
1.9.2.26.2.2 全球生态学
-
1.9.2.36.2.3 全球变化对生态系统的影响
-
1.9.2.46.2.4 生态系统对全球变化的响应
-
1.9.3思考与练习题
-
1.10第7章 干扰生态学与恢复生态学
-
1.10.17.1 干扰及其生态学意义
-
1.10.1.17.1.1 干扰的定义、类型及性质
-
1.10.1.27.1.2 干扰的生态学意义
-
1.10.27.2 人为干扰的主要形式
-
1.10.2.17.2.1 传统劳作方式对生态系统的干扰
-
1.10.2.27.2.2 环境污染
-
1.10.2.37.2.3 不断出现的新干扰形式
-
1.10.37.3 退化生态系统的定义、成因、类型和特征
-
1.10.3.17.3.1 退化生态系统的定义
-
1.10.3.27.3.2 退化生态系统的成因
-
1.10.3.37.3.3 退化生态系统的类型
-
1.10.3.47.3.4 退化生态系统的特征
-
1.10.47.4 中国的脆弱生态系统
-
1.10.57.5 恢复生态学的概念与基本理论
-
1.10.5.17.5.1 生态恢复的定义
-
1.10.5.27.5.2 生态恢复后的特征
-
1.10.5.37.5.3 恢复生态学的定义
-
1.10.5.47.5.4 恢复生态学的基本内容
-
1.10.5.57.5.5 恢复生态学的基本理论
-
1.10.67.6 受损生态系统的恢复重建
-
1.10.6.17.6.1 生态恢复的目标
-
1.10.6.27.6.2 生态恢复的基本原则
-
1.10.6.37.6.3 生态恢复成功的标准
-
1.10.6.47.6.4 生态恢复的技术方法
-
1.10.6.57.6.5 生态恢复与重建的一般操作程序
-
1.10.6.67.6.6 生态恢复的时间
-
1.10.6.77.6.7 受损生态系统的恢复实践
-
1.10.7思考与练习题
-
1.11第8章 生态系统服务功能
-
1.11.18.1 生态系统服务功能的概念与研究现状
-
1.11.1.18.1.1 生态系统服务功能的概念
-
1.11.1.28.1.2 生态系统服务功能的研究现状
-
1.11.28.2 生态系统服务功能分类
-
1.11.38.3 生态系统服务功能的评价方法
-
1.11.3.18.3.1 生态系统服务功能评价的主要方法
-
1.11.3.28.3.2 生态系统服务功能的价值评估
-
1.11.3.38.3.3 生态系统服务价值评估存在的问题和发展趋势
-
1.11.48.4 生态补偿
-
1.11.4.18.4.1 生态补偿的概念与内涵
-
1.11.4.28.4.2 生态补偿机制
-
1.11.5思考与练习题
-
1.12第9章 生态系统管理
-
1.12.19.1 生态系统管理的概念及内涵
-
1.12.1.19.1.1 生态系统管理的概念
-
1.12.1.29.1.2 生态系统管理的发展
-
1.12.1.39.1.3 生态系统管理的基本原则
-
1.12.1.49.1.4 生态系统管理的目标
-
1.12.29.2 生态系统管理的内容及途径
-
1.12.2.19.2.1 生态系统管理的基本要求
-
1.12.2.29.2.2 生态系统管理的数据基础
-
1.12.2.39.2.3 生态系统变化的度量
-
1.12.2.49.2.4 生态系统管理的要素
-
1.12.2.59.2.5 生态系统管理的主要技术与途径
-
1.12.39.3 我国几种生态系统的管理
-
1.12.3.19.3.1 农业生态系统的管理
-
1.12.3.29.3.2 森林生态系统的管理
-
1.12.3.39.3.3 城市生态系统的管理
-
1.12.3.49.3.4 旅游业生态系统的管理
-
1.12.4思考与练习题
-
1.13第10章 环境污染物及其生态效应
-
1.13.110.1 环境污染物与毒物
-
1.13.1.110.1.1 环境污染及其分类
-
1.13.1.210.1.2 环境污染物与毒物
-
1.13.1.310.1.3 主要环境污染物及其环境毒理学效应
-
1.13.210.2 污染物在环境中的迁移和转化
-
1.13.2.110.2.1 污染物在环境中的存在形态
-
1.13.2.210.2.2 污染物在环境中的迁移
-
1.13.2.310.2.3 污染物在环境中的转化
-
1.13.310.3 环境污染物的毒理学评价
-
1.13.3.110.3.1 毒理学常用的基本概念
-
1.13.3.210.3.2 毒理学常用的剂量参数
-
1.13.3.310.3.3 环境污染物的联合毒性作用
-
1.13.3.410.3.4 环境污染物毒性的评价方法
-
1.13.410.4 生态监测
-
1.13.4.110.4.1 生态监测的概念与原理
-
1.13.4.210.4.2 生态监测的类型
-
1.13.4.310.4.3 生态监测的内容、特点与任务
-
1.13.4.410.4.4 生态监测的指标体系及技术
-
1.13.510.5 生态风险评价
-
1.13.5.110.5.1 生态风险评价的主要内容
-
1.13.5.210.5.2 生态风险评价的一般程序与过程
-
1.13.6思考与练习题
-
1.14第11章 可持续发展
-
1.14.111.1 可持续发展理论
-
1.14.1.111.1.1 可持续发展的概念与内涵
-
1.14.1.211.1.2 可持续发展的度量与指标
-
1.14.211.2 社会-经济-自然复合生态系统原理
-
1.14.2.111.2.1 社会-经济-自然复合生态系统的组成与结构
-
1.14.2.211.2.2 复合生态系统的演化及动力学机制
-
1.14.2.311.2.3 复合生态系统生态控制论原理
-
1.14.311.3 生态规划
-
1.14.3.111.3.1 生态规划的概念与发展
-
1.14.3.211.3.2 生态规划的程序与内容
-
1.14.411.4 生态工程
-
1.14.4.111.4.1 生态工程的概念与发展
-
1.14.4.211.4.2 生态工程的基本原理
-
1.14.4.311.4.3 生态工程的类型
-
1.14.4.411.4.4 生态工程的发展趋势
-
1.14.511.5 产业生态学与生态产业
-
1.14.5.111.5.1 产业生态学
-
1.14.5.211.5.2 生态产业
-
1.14.6思考与练习题
-
1.15参考文献
1
环境生态学