-
1.1前 言
-
1.2上篇 信息技术基础理论
-
1.2.11 计算机与信息技术概述
-
1.2.1.11.1 计算机发展概述
-
1.2.1.1.11.1.1 计算机的产生和发展
-
1.2.1.1.21.1.2 微电子技术
-
1.2.1.1.31.1.3 计算机的特点
-
1.2.1.1.41.1.4 计算机的发展趋势
-
1.2.1.21.2 计算机的分类
-
1.2.1.31.3 计算机的应用
-
1.2.1.41.4 信息技术的基本概念
-
1.2.1.4.11.4.1 什么是信息
-
1.2.1.4.21.4.2 信息技术
-
1.2.1.51.5 信息在计算机中的表示
-
1.2.1.5.11.5.1 数制及转换
-
1.2.1.5.21.5.2 信息的计量单位
-
1.2.1.5.31.5.3 数值信息的表示
-
1.2.1.5.41.5.4 字符信息的表示
-
1.2.1.6习题一
-
1.2.22 计算机硬件系统
-
1.2.2.12.1 计算机硬件系统的组成
-
1.2.2.1.12.1.1 中央处理器
-
1.2.2.1.22.1.2 存储器
-
1.2.2.1.32.1.3 输入/输出设备
-
1.2.2.1.42.1.4 主板
-
1.2.2.1.52.1.5 总线与接口
-
1.2.2.22.2 计算机的工作原理
-
1.2.2.2.12.2.1 指令和指令系统
-
1.2.2.2.22.2.2 计算机的工作原理
-
1.2.2.3习题二
-
1.2.33 计算机软件
-
1.2.3.13.1 什么是计算机软件
-
1.2.3.1.13.1.1 软件及其组成
-
1.2.3.1.23.1.2 软件的分类
-
1.2.3.1.33.1.3 软件的版权问题
-
1.2.3.1.43.1.4 软件危机
-
1.2.3.23.2 系统软件
-
1.2.3.2.13.2.1 操作系统
-
1.2.3.2.23.2.2 常用操作系统
-
1.2.3.33.3 应用软件
-
1.2.3.43.4 常用工具软件功能介绍
-
1.2.3.53.5 程序设计
-
1.2.3.5.13.5.1 程序设计语言
-
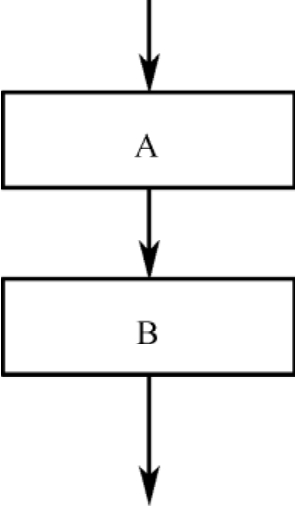
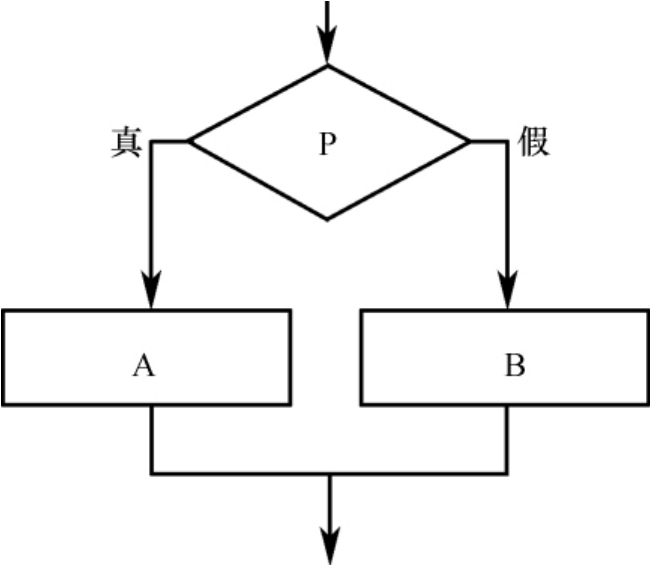
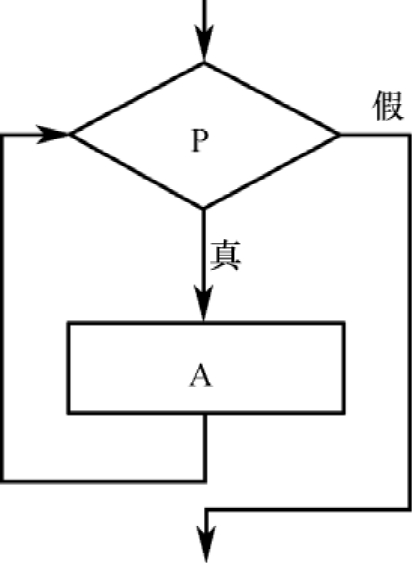
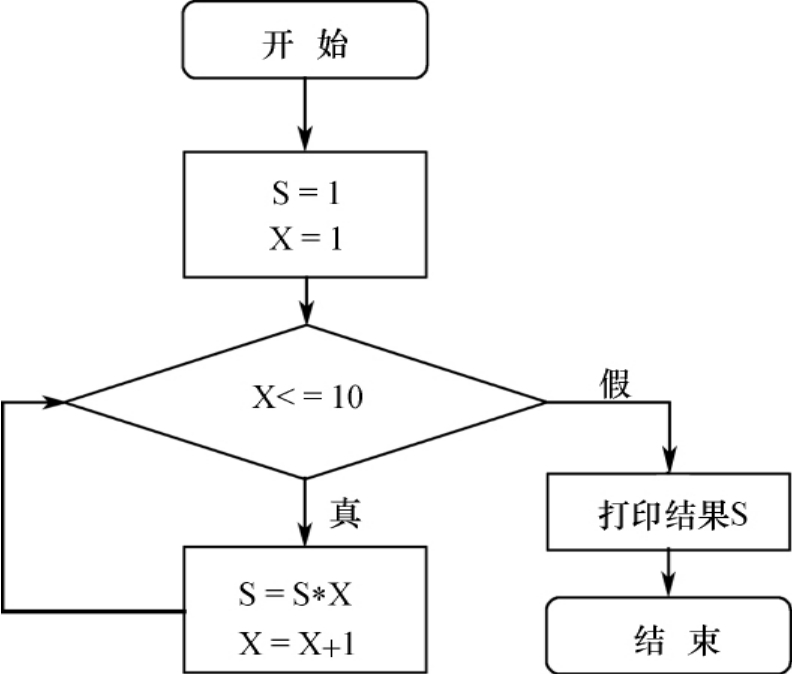
1.2.3.5.23.5.2 算法
-
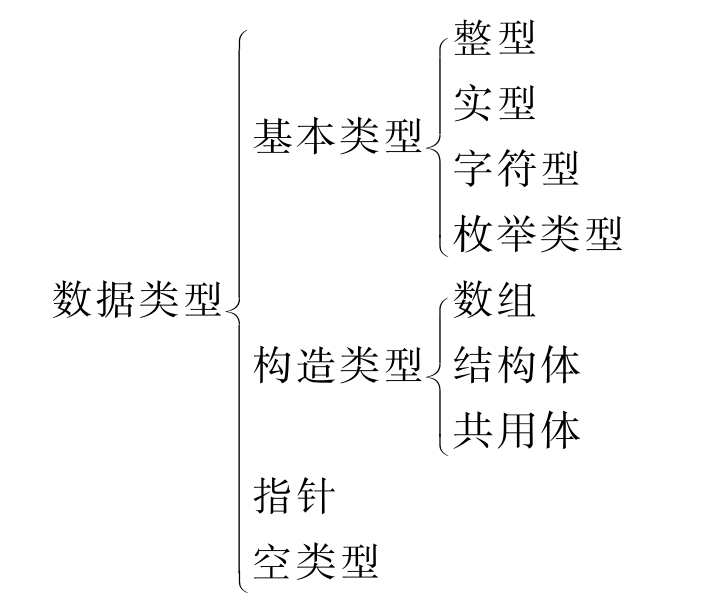
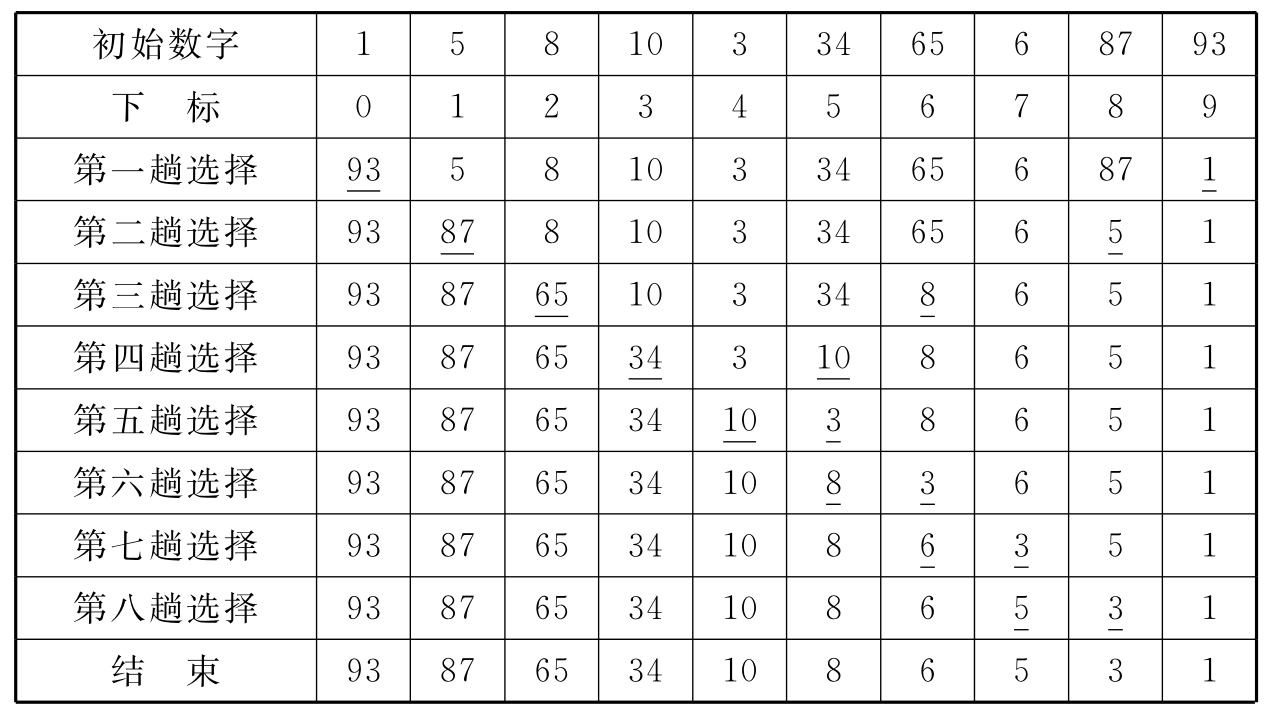
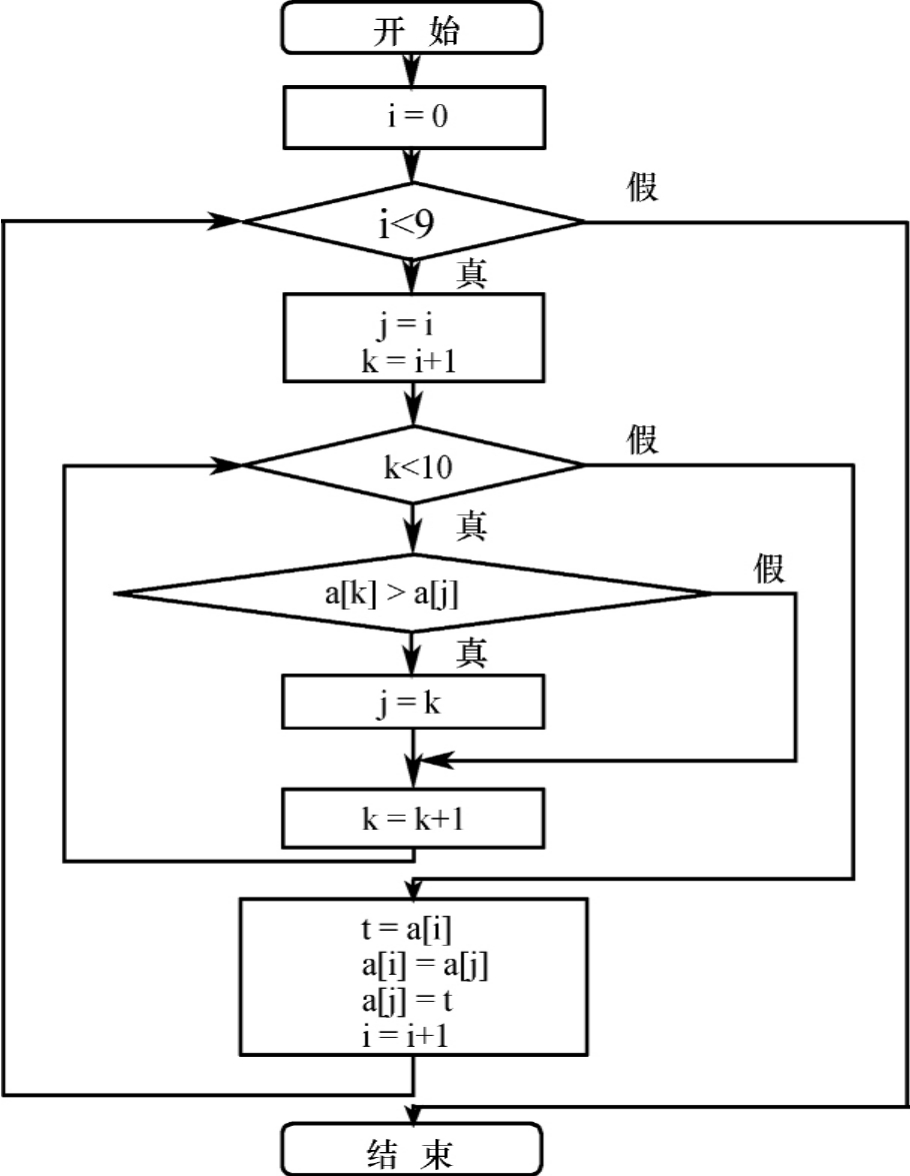
1.2.3.5.33.5.3 数据结构
-
1.2.3.63.6 软件工程
-
1.2.3.6.13.6.1 软件的生命周期
-
1.2.3.6.23.6.2 软件开发的原则
-
1.2.3.7习题三
-
1.2.44 计算机网络与Internet应用
-
1.2.4.14.1 计算机网络基础知识
-
1.2.4.1.14.1.1 计算机网络的形成和发展
-
1.2.4.1.24.1.2 计算机网络的定义和功能
-
1.2.4.1.34.1.3 计算机网络的分类
-
1.2.4.1.44.1.4 计算机网络的组成
-
1.2.4.1.54.1.5 计算机网络应用模式
-
1.2.4.24.2 数据通信基础知识
-
1.2.4.2.14.2.1 数据通信基本概念
-
1.2.4.2.24.2.2 通信介质
-
1.2.4.2.34.2.3 数据通信基本技术
-
1.2.4.34.3 局域网
-
1.2.4.3.14.3.1 局域网的主要特征
-
1.2.4.3.24.3.2 局域网的组成
-
1.2.4.3.34.3.3 常见的局域网
-
1.2.4.44.4 Internet基础
-
1.2.4.4.14.4.1 Internet的产生和发展
-
1.2.4.4.24.4.2 Internet的体系结构
-
1.2.4.4.34.4.3 Internet的地址和域名
-
1.2.4.54.5 接入Internet的方法
-
1.2.4.64.6 Internet的服务与应用
-
1.2.4.6.14.6.1 WWW服务
-
1.2.4.6.24.6.2 电子邮件服务
-
1.2.4.6.34.6.3 文件传输服务
-
1.2.4.6.44.6.4 电子公告板服务
-
1.2.4.74.7 计算机网络安全
-
1.2.4.7.14.7.1 计算机网络安全概述
-
1.2.4.7.24.7.2 数据加密
-
1.2.4.7.34.7.3 防火墙技术
-
1.2.4.7.44.7.4 计算机病毒及防范
-
1.2.4.8习题四
-
1.2.55 多媒体技术及应用
-
1.2.5.15.1 多媒体基本概念
-
1.2.5.25.2 超文本
-
1.2.5.2.15.2.1 超文本的概念
-
1.2.5.2.25.2.2 超媒体的概念
-
1.2.5.2.35.2.3 超文本标记语言(HTML)
-
1.2.5.35.3 图形图像基础
-
1.2.5.3.15.3.1 数字图像的类别和获取
-
1.2.5.3.25.3.2 图像表示
-
1.2.5.3.35.3.3 图像压缩编码
-
1.2.5.3.45.3.4 数字图像处理与应用
-
1.2.5.3.55.3.5 计算机图形学与图形处理技术
-
1.2.5.45.4 数字音频基础
-
1.2.5.4.15.4.1 音频的输入与输出
-
1.2.5.4.25.4.2 音频压缩编码与常用格式
-
1.2.5.4.35.4.3 常用音频编辑软件
-
1.2.5.4.45.4.4 音频合成技术与语音识别技术
-
1.2.5.55.5 数字视频技术
-
1.2.5.5.15.5.1 数字视频基础
-
1.2.5.5.25.5.2 数字视频的压缩编码
-
1.2.5.5.35.5.3 数字视频编辑技术
-
1.2.5.5.45.5.4 数字视频合成技术
-
1.2.5.5.55.5.5 数字视频应用
-
1.2.5.6习题五
-
1.2.66 数据库技术与信息系统
-
1.2.6.16.1 数据库系统概述
-
1.2.6.1.16.1.1 数据库系统基本概念
-
1.2.6.1.26.1.2 数据库技术的产生和发展
-
1.2.6.1.36.1.3 数据库系统的特点
-
1.2.6.26.2 关系数据模型
-
1.2.6.2.16.2.1 数据模型的概念
-
1.2.6.2.26.2.2 数据模型的分类
-
1.2.6.2.36.2.3 概念数据模型
-
1.2.6.2.46.2.4 关系数据模型简介
-
1.2.6.36.3 关系代数操作
-
1.2.6.3.16.3.1 传统的集合运算
-
1.2.6.3.26.3.2 专门的关系运算
-
1.2.6.46.4 SQL概述
-
1.2.6.4.16.4.1 SQL的特点
-
1.2.6.4.26.4.2 SQL语言的基本概念
-
1.2.6.4.36.4.3 数据定义语句
-
1.2.6.4.46.4.4 查询
-
1.2.6.4.56.4.5 数据更新
-
1.2.6.4.66.4.6 视图
-
1.2.6.56.5 信息系统
-
1.2.6.5.16.5.1 信息的概念和特征
-
1.2.6.5.26.5.2 信息系统的概念
-
1.2.6.5.36.5.3 信息系统的类型
-
1.2.6.5.46.5.4 信息系统与数据库的关系
-
1.2.6.5.56.5.5 信息系统的开发过程
-
1.2.6.5.66.5.6 信息系统开发工具简介
-
1.2.6.5.76.5.7 信息系统发展趋势
-
1.2.6.6习题六
-
1.3下篇 实验指导
-
1.3.17 WindowsXP的基本应用
-
1.3.1.1实验一 Windows的基本操作
-
1.3.1.2实验二 资源管理器、文件管理和控制面板的使用
-
1.3.28 Word2003的使用
-
1.3.2.1实验一 Word的基本操作
-
1.3.2.2实验二 Word的环境设置
-
1.3.2.3实验三 Word的文本编辑
-
1.3.2.4实验四 Word的编辑进阶
-
1.3.2.5实验五 表格的使用
-
1.3.2.6实验六 图文混排与打印
-
1.3.39 Excel2003的使用
-
1.3.3.1实验一 Excel表格数据录入和格式化
-
1.3.3.2实验二 Excel公式、函数的使用方法
-
1.3.3.3实验三 Excel图表使用方法
-
1.3.3.4实验四 分类汇总和数据透视表操作
-
1.3.410 PowerPoint2003的使用
-
1.3.4.1实验一 新建演示文稿
-
1.3.4.2实验二 修饰演示文稿
-
1.3.4.3实验三 演示文稿高级制作
-
1.3.511 FrontPage2003的使用
-
1.3.5.1实验一 FrontPage基本操作
-
1.3.5.2实验二 FrontPage高级应用
-
1.3.612 IE浏览器的使用及OutlookExpress邮件管理
-
1.3.6.1实验一 IE浏览器的使用
-
1.3.6.2实验二 OutlookExpress邮件管理
-
1.3.713 多媒体软件的使用
-
1.3.7.1实验一 Flash动画制作
-
1.3.7.2实验二 用Photoshop制作水彩画
-
1.3.8参考文献
1
大学信息技术基础教程