-
1.1内容简介
-
1.2出版说明
-
1.3前 言
-
1.4第一章 MATLAB基础
-
1.4.11.1 MATLAB历史背景
-
1.4.21.2 MATLAB概述
-
1.4.31.3 MATLAB安装
-
1.4.41.4 MATLAB的启动与退出
-
1.4.51.5 MATLAB的应用窗口
-
1.4.61.6 MATLAB语言初步
-
1.4.71.7 程序结构
-
1.4.81.8 部分基本数学函数和基本作图函数
-
1.4.91.9 编制函数
-
1.5第二章 数字信号处理与MATLAB信号处理基础
-
1.5.12.1 基本信号序列
-
1.5.22.2 一些基本序列的生成
-
1.5.32.3 离散序列的基本运算
-
1.5.42.4 时域信号的抽样与重建
-
1.5.52.5 离散傅里叶变换(DFT)
-
1.5.62.6 快速傅里叶变换(FFT)
-
1.6第三章 离散线性非时变系统分析
-
1.6.13.1 线性时不变系统
-
1.6.23.2 卷积和原理及其应用
-
1.6.33.3 离散LTI系统的冲激响应和阶跃响应
-
1.6.43.4 离散LTI系统的零极点分析
-
1.6.53.5 离散系统的差分方程表示及求解
-
1.7第四章 IIR滤波器的设计
-
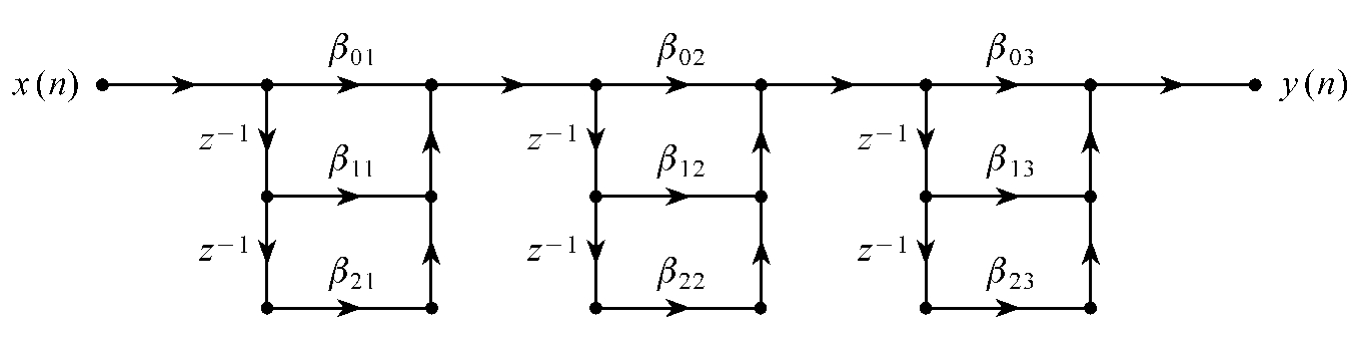
1.7.14.1 IIR滤波器的网络结构
-
1.7.24.2 IIR滤波器的设计
-
1.7.34.3 IIR滤波器的直接设计
-
1.7.44.4 关于MATLAB函数的一些其他的用法
-
1.8第五章 FIR滤波器的设计
-
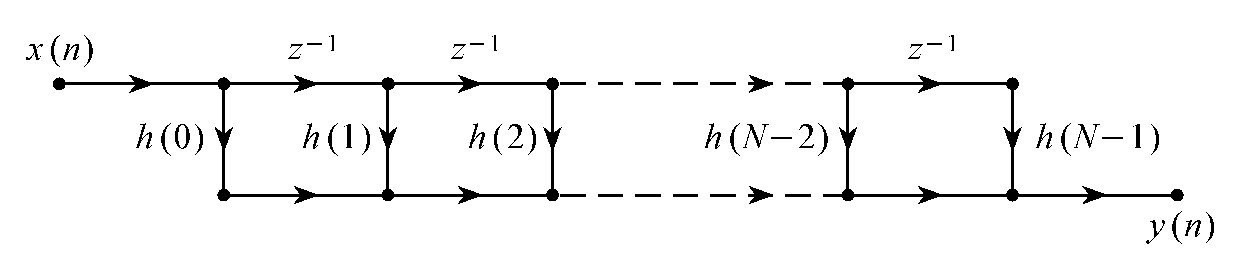
1.8.15.1 FIR滤波器的网络结构
-
1.8.25.2 FIR滤波器的设计
-
1.9第六章 图形化信号处理设计工具——SPTool
-
1.9.16.1 SPTool工具介绍
-
1.9.26.2 信号浏览器
-
1.9.36.3 滤波器浏览器和滤波器设计器
-
1.9.46.4 频谱浏览器
-
1.9.56.5 综合实例
-
1.10附录 MATLAB信号处理工具箱函数
-
1.11参考文献
1
MATLAB与数字信号处理实验