-
1.1目录
-
1.2内 容 简 介
-
1.3前 言
-
1.4第1章 绪 论
-
1.4.11.1 本章内容回顾
-
1.4.1.11.1.1 基本概念及有关术语
-
1.4.1.21.1.2 重点难点
-
1.4.21.2 习题解答
-
1.5第2章 线 性 表
-
1.5.12.1 本章内容回顾
-
1.5.1.12.1.1 线性表的存储结构
-
1.5.1.22.1.2 线性表插入和删除运算
-
1.5.22.2 习题解答
-
1.5.2.12.2.1 概念题
-
1.5.2.22.2.2 算法设计
-
1.5.32.3 实验指导
-
1.5.3.12.3.1 实验目的
-
1.5.3.22.3.2 实验内容
-
1.5.3.32.3.3 基本要求
-
1.5.3.42.3.4 实验提示
-
1.6第3章 栈和队列
-
1.6.13.1 本章内容回顾
-
1.6.1.13.1.1 栈的基本知识
-
1.6.1.23.1.2 顺序栈的基本操作实现
-
1.6.1.33.1.3 链栈的基本操作实现
-
1.6.1.43.1.4 队列的基本知识
-
1.6.1.53.1.5 顺序队列
-
1.6.1.63.1.6 循环队列
-
1.6.1.73.1.7 链队列
-
1.6.23.2 习题解答
-
1.6.33.3 实验指导
-
1.6.3.13.3.1 实验目的
-
1.6.3.23.3.2 实验内容
-
1.6.3.33.3.3 算法描述
-
1.7第4章 其他线性数据结构
-
1.7.14.1 本章内容回顾
-
1.7.1.14.1.1 基本概念
-
1.7.1.24.1.2 重点难点
-
1.7.24.2 习题解答
-
1.7.34.3 实验指导
-
1.7.3.14.3.1 实验目的
-
1.7.3.24.3.2 实验内容
-
1.7.3.34.3.3 基本要求
-
1.7.3.44.3.4 实验提示
-
1.8第5章 树与二叉树
-
1.8.15.1 本章内容回顾
-
1.8.1.15.1.1 基本概念
-
1.8.1.25.1.2 重点难点
-
1.8.25.2 习题解答
-
1.8.35.3 实验指导
-
1.8.3.15.3.1 实验目的
-
1.8.3.25.3.2 实验内容
-
1.8.3.35.3.3 基本要求
-
1.8.3.45.3.4 实验提示
-
1.9第6章 图
-
1.9.16.1 本章内容回顾
-
1.9.1.16.1.1 基本概念
-
1.9.1.26.1.2 重点难点
-
1.9.26.2 习题解答
-
1.9.36.3 实验指导
-
1.9.3.16.3.1 实验目的
-
1.9.3.26.3.2 实验内容
-
1.9.3.36.3.3 基本要求
-
1.9.3.46.3.4 实验提示
-
1.10第7章 查 找
-
1.10.17.1 本章内容回顾
-
1.10.1.17.1.1 基本概念
-
1.10.1.27.1.2 静态查找表
-
1.10.1.37.1.3 动态查找表
-
1.10.1.47.1.4 哈希查找
-
1.10.1.57.1.5 本章重点、难点
-
1.10.27.2 习题解答
-
1.10.37.3 实验指导
-
1.10.3.17.3.1 实验目的
-
1.10.3.27.3.2 实验内容
-
1.10.3.37.3.3 实验过程
-
1.11第8章 排 序
-
1.11.18.1 本章内容回顾
-
1.11.1.18.1.1 基本概念
-
1.11.1.28.1.2 重点难点
-
1.11.28.2 习题解答
-
1.11.38.3 实验指导
-
1.11.3.18.3.1 实验目的
-
1.11.3.28.3.2 实验内容
-
1.11.3.38.3.3 基本要求
-
1.11.3.48.3.4 快速排序实验过程及实现函数
-
1.11.3.58.3.5 堆排序的实现过程及实现函数
-
1.12第9章 文 件
-
1.12.19.1 本章内容回顾
-
1.12.1.19.1.1 基本概念
-
1.12.1.29.1.2 重点与难点
-
1.12.29.2 习题解答
-
1.13参 考 文 献
1
《数据结构(C++版)》复习提要与实验指导
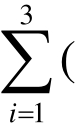 ( i-1)ni=1+(1-1)·2+(2-1)·1+(3-1)·2=6,故选C。
( i-1)ni=1+(1-1)·2+(2-1)·1+(3-1)·2=6,故选C。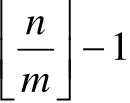
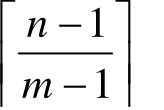 D.
D.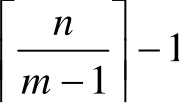
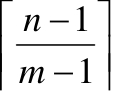 次合并,每次合并增加一个非叶节点。故选C。
次合并,每次合并增加一个非叶节点。故选C。