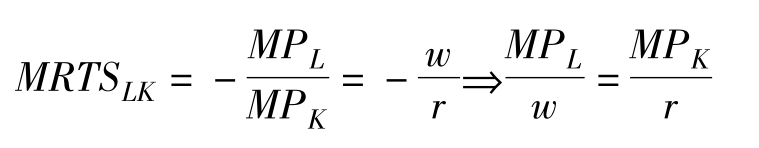第二节 生产者最优产量的选择
从经济学角度来讲,生产的含义是十分广泛的,它不仅仅意味着制造了一台机器或生产出一些钢材等,它还包含了各种各样的经济活动。如:律师为他人打官司,商场的经营,医生为病人看病等等。这些活动都涉及某个人或经济实体提供产品或服务。因此,简单讲,任何创造价值的活动都是生产。任何生产者都希望通过理性选择合理安排生产要素,以达到最大化的产量。本节探讨的核心问题是要达到最优产量,生产者应如何选择投入生产要素。
一、生产函数
生产函数表示在技术水平一定的前提下,投入不同数量的生产要素,所能生产某种商品的最大数量。通常表示为:Q=f(L,K,N,E)。
上式中,各变量分别代表产量、投入的劳动、资本、土地和企业家才能。其中土地N是固定的,企业家才能E难以估算,所以生产函数一般简化为Q=f(L,K)。
(一)常见的生产函数
1.线性生产函数
线性生产函数一般表示为Q=aL+bK,其中a、b均为常数,产量Q则表现为劳动力L和资本K的正向函数,即劳动和资本的增加将带来产量的增加。
2.柯布-道格拉斯生产函数
柯布-道格拉斯生产函数是由数学家柯布(C.W.Cobb)和经济学家道格拉斯(Paul H.Douglas)于20世纪30年代提出来的,表示为Q=ALαKβ,其中一般认为A为常数,α+β=1,不同行业的A、α和β值不同。柯布-道格拉斯生产函数被认为是一种很有用的生产函数,因为该函数以其简单的形式具备了经济学家所关心一些性质,它在经济理论的分析和应用中都具有一定意义。
生活中的经济学
柯布和道格拉斯
柯布和道格拉斯研究的是1899年至1922年美国制造业的生产函数。他们指出,制造业的投资分为以机器和建筑物为主要形式的固定资本投资和以原料、半成品和仓库里的成品为主要形式的流动资本投资,同时还包括对土地的投资。他们认为,在商品生产中起作用的资本,不包括流动资本。他们认为流动资本属于制造过程的结果,而非原因。他们还排除了对土地的投资,因其认为这部分投资受土地价值异常增值的影响较大。
在他们的生产函数中,资本这一要素只包括对机器、工具、设备和工厂建筑的投资。而对劳动这一要素的度量,选用的是制造业的雇佣工人数。
但由于当时对这些生产要素的统计既非每年连续的,也非恰好按他们的分析需要分类统计的,故不得不尽力利用现有的其他数据以估计出他们打算使用的数据数值。比如,用生铁、钢、钢材、木材、焦炭、水泥、砖和铜等用于生产机器和建筑物的原料的数量变化来估计机器和建筑物的数量的变化;用美国一两个州的雇佣工人数的变化来代表整个美国的雇佣工人数的变化等。
经过处理得出关于1899年至1922年间,产出量P、资本K和劳动L的相对变化的数据(以1899年为基准),并从这些数据中得出生产函数公式:
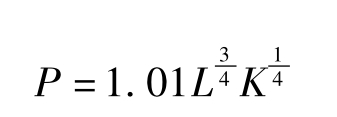
此结果虽与现代计算机统计软件的计算结果不同,但无本质差别。但他们却被自己的结论吓坏了,他们发现不仅资本能“创造”价值,且产出的大部分,即3/4的产出都应归属于劳动。在资本家横行年代,这个结论显然不受欢迎,他们不得不表示自己千辛万苦得到的这个结果值得怀疑,强调他们的文章不在于给出结论,而在于演示方法。
(二)短期生产函数和长期生产函数
(1)长期(Long-run):指时间长到可以使厂商调整生产规模来达到调整产量的目的。在长期中,一切生产要素都是可以变动的,不仅劳动投入量、原材料使用量可变,而且资本、设备量也可变。
(2)短期(Short-run):指时间短到厂商来不及调整生产规模来达到调整产量的目的,而只能在原有厂房、机器、设备条件下来调整产量。在短期中,只有一部分要素如劳动投入量及原材料数量是可变的,而另一些生产要素不随产量变动而变动,如机器、厂房、设备、高级管理人才等。
(3)长短期的相对性:“短期”、“长期”的区分是相对的。在有些生产部门中,如在钢铁工业、机器制造业等部门中,所需资本设备数量多,技术要求高,变动生产规模不容易,则几年也许算是“短期”;反之,有些行业如普通服务业、食品加工业,所需资本设备数量少,技术要求低,变动生产规模比较容易,也许几个月可算是“长期”。
生产中两种最重要的投入是劳动与资本,因此,在经济分析中,通常假定企业只使用这两种要素。在短期内,假设资本数量不变,只有劳动可随产量变化,则生产函数可表示为Q=f(L),这种生产函数可称为短期生产函数。在长期,资本和劳动都可变,则生产函数可表示为Q=f(L,K),这种生产函数可称为长期生产函数。
二、短期生产函数
讨论短期生产函数的时候,我们假设只有一种可变要素,通常为劳动力,其他要素都是固定的。此时企业的理性选择就在于究竟在现有技术和生产规模的前提下,投入多少劳动力是最经济的。
(一)总产量、平均产量与边际产量
(1)总产量:用TP表示,是指企业在一定时期生产的产量总和。公式表示为TP=f(L)。例如某林场,3名伐木工人,每天可以伐木900立方米,5名伐木工人,每天可以伐木1850立方米。则说明,当投入3名劳动力时,总产量TP=900立方米,当投入5名劳动力时,总产量TP增加为1850立方米。
(2)平均产量:是指平均每单位变动投入所生产的产量。公式表示为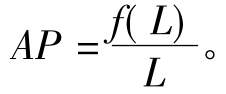
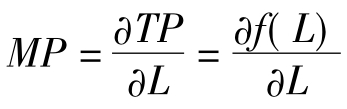
在上述案例中,伐木工人数量为3人时,平均每个工人伐木的数量为300立方米;伐木工人数量为5人时,平均每个工人伐木的数量为370立方米。
(3)边际产量:是指每增加一单位某种投入所增加的产量。边际产量用MP表示,公式表示为。在上述案例中,假如投入4个劳动力时,总产量TP=1400,那么第4个劳动力的边际产量MP为500=1400-900立方米,第5个劳动力的边际产量MP为450=1850-1400立方米。
(二)生产要素的边际产量递减规律
也叫报酬递减规律,是指在技术水平和其他要素投入固定不变,只有一种要素投入可以变动时,随着该可变要素投入的增加,其边际产量即每增加一单位可变要素投入所增加的总产量越来越少。关于要素的边际报酬递减规律要注意以下三点:
第一,要素的边际报酬递减规律以技术水平和其他要素投入固定不变为前提条件。若技术水平和其他要素投入发生变化,这个规律就不起作用。
第二,随着某种变动要素投入的连续增加,边际报酬的变动要经历递增和递减两个阶段。这是因为技术系数可变的生产函数在一定的技术条件下,各种要素投入客观上存在一个最优比例关系,例如在上述林场中,由于伐木设备是有限的,可能8个伐木工人的配合是最有效率的,如果人太多了就会导致当无法细分的固定要素投入过多而变动要素投入过少时,增加变动投入就能充分发挥固定要素的潜在效率,导致变动要素的边际报酬递增。一旦固定要素的潜在效率随着变动要素的连续增加而充分发挥出来以后,再增加变动要素投入,边际报酬就开始递减。
第三,边际报酬递减规律同边际效用递减规律一样,都是公理,无需证明。
生活中的经济学
施肥与产量
边际产量递减规律是从社会生产实践和科学实验中总结出来的,在现实生活的绝大多数生产过程中都是适用的。早在1771年英国农学家杨格就用在若干相同的地块上施以不同量肥料的实验,证明了肥料施用量与产量增加之间存在着这种边际产量递减的关系。这不是偶然的现象而是经验性规律。农民在一亩土地上撒一把化肥能增加产量1公斤,撒两把化肥增产3公斤,但一把一把化肥的增产效果会越来越差,过量的施肥量甚至导致土壤板结粮食减产。如果是边际产量递增全世界有一亩土地就能养活全世界所有的人,那才是不可思议的了。
(三)总产量、平均产量和边际产量之间的关系
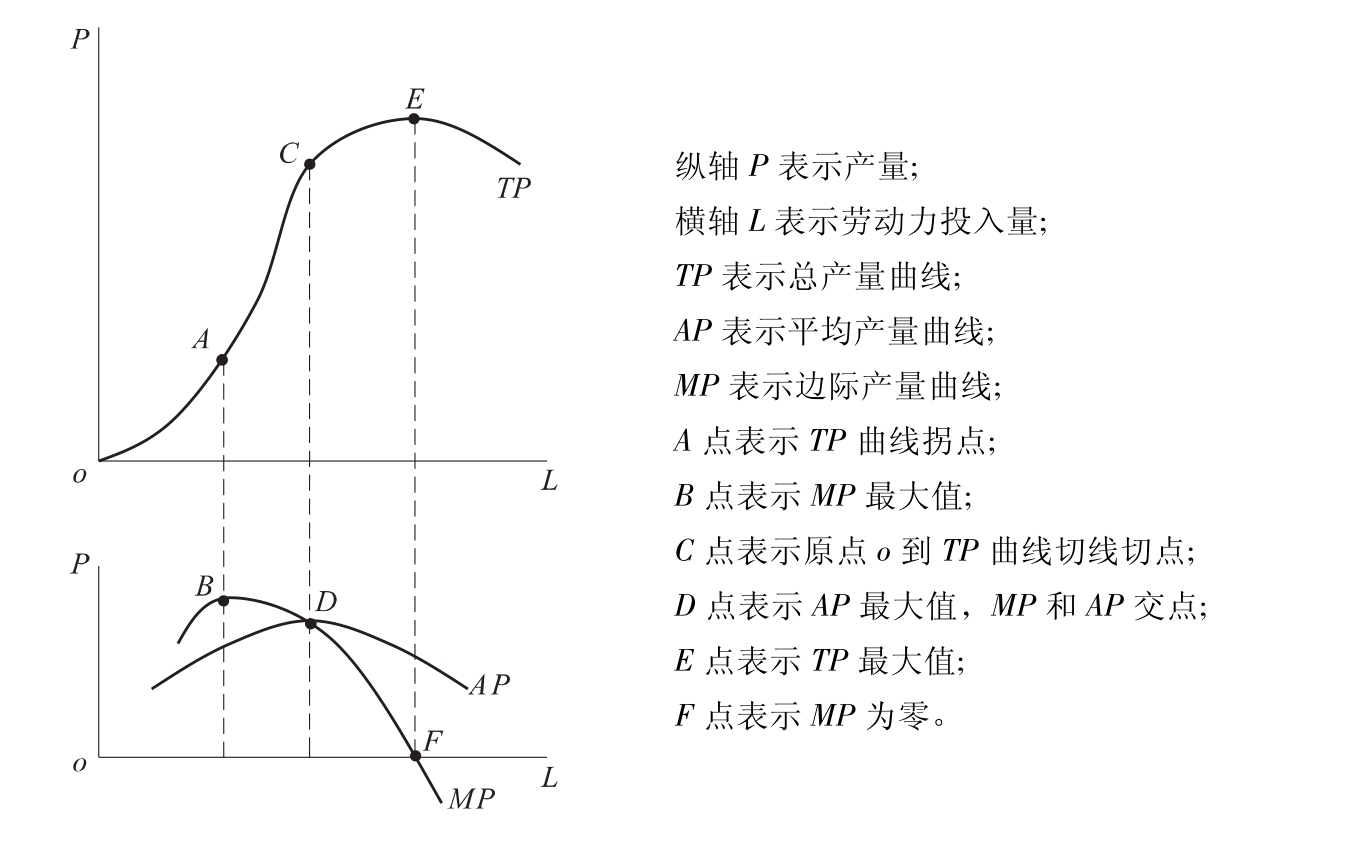
图4-2 总产量、平均产量和边际产量
1.总产量与边际产量的关系
当边际产量增加、边际产量曲线上升时,如图4-2中的OA段,总产量以递增的速度增加,总产量曲线上凹地向右上方伸展;当边际产量递减且大于零时,如图4-2中的AC段,总产量以递减的速度增加,总产量曲线下凹地向右上方延伸;边际产量等于零时,如图4-2中的EF,总产量达到极大。一旦边际产量小于零,总产量就减少,总产量曲线就开始下降。
从边际产量的计算公式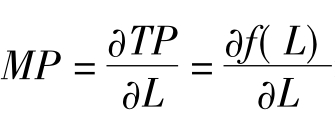 看,边际产量就是总产量曲线的斜率。由于总产量曲线先上凹后下凹,故在总产量曲线的拐点A,斜率极大,即边际产量极大。在此以前,斜率递增,即边际产量递增。此点以后,斜率递减,即边际产量递减。
看,边际产量就是总产量曲线的斜率。由于总产量曲线先上凹后下凹,故在总产量曲线的拐点A,斜率极大,即边际产量极大。在此以前,斜率递增,即边际产量递增。此点以后,斜率递减,即边际产量递减。
2.总产量与平均产量之间的关系
因为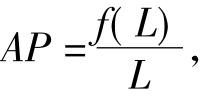 所以平均产量就是从原点向总产量曲线所作射线的斜率。由于总产量曲线先上凹后下凹,故从原点向总产量曲线所作的射线正好切于总产量曲线时,射线的斜率极大,即平均产量极大。在切点C以前,射线的斜率递增,即平均产量递增。在切点C以后,射线的斜率递减,即平均产量递减。
所以平均产量就是从原点向总产量曲线所作射线的斜率。由于总产量曲线先上凹后下凹,故从原点向总产量曲线所作的射线正好切于总产量曲线时,射线的斜率极大,即平均产量极大。在切点C以前,射线的斜率递增,即平均产量递增。在切点C以后,射线的斜率递减,即平均产量递减。
3.平均产量和边际产量之间的关系
从原点向总产量曲线所作的射线正好切于总产量曲线时,不仅射线的斜率极大,而且射线与总产量曲线的切线重合。射线的斜率就是平均产量,射线的斜率极大,意味着平均产量极大。而切线的斜率就是边际产量。因此平均产量最大时,平均产量正好等于边际产量,即边际产量曲线交于平均产量曲线的最高点D。在交点D以前,边际产量大于平均产量,使平均产量递增。在交点D以后,边际产量小于平均产量,使平均产量递减。
生活中的经济学
转盘的生产
转盘是某大型连续卷管机400多种零件中的关键零件之一,用4台机床进行加工。开始时用4名工人加工,一人一台机床。由于每个人既要操作机床,又要做必要的辅助工作(如卡零件、借用工具、相互传递、打扫卫生等),使机床生产效率未得到充分发挥,日总产量32件,人均产量8件。当增加一人后,就可有一人做辅助工作,其他4人能把大部分时间用在机床上,日总产量增到41件,人均产量8.2件,边际产量9件。再增加一人后,就能承担绝大部分辅助工作,有4人盯住机床,充分发挥设备效率,日总产量又增至54件,人均产量9件,边际产量为13件。这是边际实际报酬的递增阶段,总产量以递增的速度增加。
当增加到7人时,由于新投入的第三个人只能担负一部分辅助工作,有一部分时间没活干,因此总产量虽然增至63件,平均产量保持不变,边际产量反而下降。此后,随着投入的劳动力进一步增加,不但剩余时间越来越多,且互相干扰,废品率相应上升,平均产量不断下降,边际产量速降。直到总劳动力为10人时,总产量最大,平均产量从递增到递减,边际产量从最大到0。当劳动力增至10人以上时,便人浮于事,人多手杂,职责不清,互相扯皮,废品率进一步增加,边际产量为负,平均产量继续下降,总产量也开始下降,出现了负报酬阶段。
讨论
如果你负责招聘,那么雇用多少劳动力才能达到企业的最大利益?
(四)只有一种要素变化时生产者最优产量的选择
在短期生产函数中,只有一种生产要素——劳动力L发生变动,其他要素固定不变的短期生产函数中,整个生产过程根据总产量、平均产量和边际产量的变化情况,可以分为三个阶段:
Ⅰ区,位于虚线CD的左侧,此时总产量和平均产量均处于上升状态,边际产量先上升,再下降;
Ⅱ区,位于虚线CD和EF的中间,此时总产量处于上升状态并逐渐达到最大值,平均产量由最大值点开始下降,边际产量持续下降,并达到零值;
Ⅲ区,总产量和平均产量均处于下降状态,边际产量为负值。
如图4-3所示。
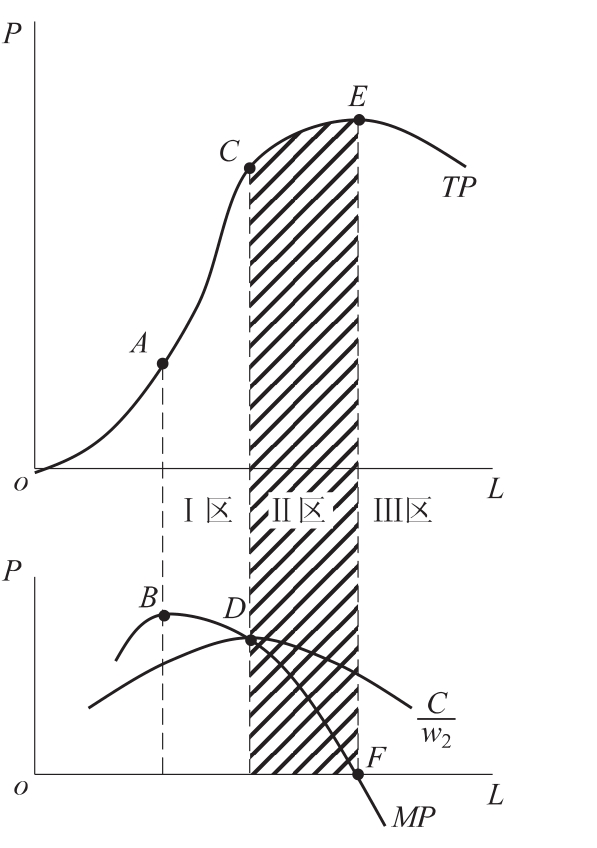
图4-3 短期生产函数的理性决策区域
我们通常把Ⅰ、Ⅱ、Ⅲ区分别称为成长阶段、成熟阶段和衰退阶段,短期生产函数中理性决策区域是Ⅱ区,也就是理性的厂商会把劳动力的投入量选择在成熟阶段,此时平均产量递减,边际产量大于零,总产量逐渐达到最大值。厂商的决策不会考虑第三阶段是因为,在第三阶段由于边际产量递减且小于零,意味着增加劳动力的投入将使总产量减少,说明目前设备的产能已经超过最优状态,劳动力增加,效率越低。厂商也不会选择第一阶段是因为,在这个阶段平均产量处于递增状态,厂商增加劳动力的投入就能带来平均产量和总产量的双层增加,此时如果要素价格和产品价格既定不变,并且产品总可以销售出去,厂商的利润就会随着平均产量的增加而增加。因此,厂商就必然会增加变动投入,从而进入第二阶段。
在Ⅱ区中究竟企业会选择左边线CD还是右边线EF来作为劳动力投入量的决策点呢,这要看企业的目标,在追求总收益最大的时候,会选择右边线EF,即总产量达到最大值的劳动力投入量;在追求平均成本最小时,会选择左边线CD,即平均产量最大值的劳动力投入量。
三、长期生产函数
长期中,所有的投入都可以随着产量的变动而变动,厂商可以通过扩建厂房、引入新的生产线等方式改变产量,在此我们分析只有资本K和劳动力L发生变化的生产函数,公式表示为Q=f(L,K),如何组合劳动力和资本的数量才能够在成本一定的时候获得最大产量,或者在产量一定的时候花费最小成本,我们将通过等产量线、等成本线及其均衡来进行分析。
(一)等产量曲线
等产量曲线是指在技术水平不变的条件下,能给厂商带来相同产量水平的两种要素组合的轨迹。如图4-4所示。

图4-4 等产量线
1.边际技术替代率
资本和劳动力两种生产要素可以相互替代,都完成同样的产量,不同国家和地区由于资本和劳动力的价格不同,会选择两种要素不同比例的组合;即使是同一个厂商,如果要素中的一种价格发生了变化,为了追求最优生产效率,厂商也会对要素的投入比例进行调整。在技术和产量不变的条件下,厂商为增加一单位某种要素的投入所能减少的另一种要素的投入量就是边际技术替代率。
劳动对资本的边际技术替代率常用MRTSLK表示,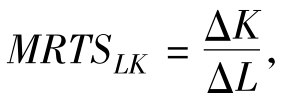 也可以表示为
也可以表示为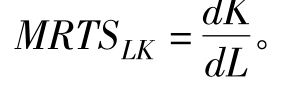 由于边际报酬递减,当厂商不断地用劳动替代资本时,随着劳动投入的增加,劳动的边际产量日益减少;随着资本投入的减少,资本的边际产量日益增加。因此,边际技术替代率具有递减的趋势。如图4-5所示。
由于边际报酬递减,当厂商不断地用劳动替代资本时,随着劳动投入的增加,劳动的边际产量日益减少;随着资本投入的减少,资本的边际产量日益增加。因此,边际技术替代率具有递减的趋势。如图4-5所示。

图4-5 边际技术替代率
2.等产量曲线的特征
(1)离远点越远,产量越高
在同一等产量曲线图中,有无数条等产量曲线。离原点更远的等产量曲线拥有更多的要素投入量,因而代表着更高的产量水平。
(2)等产量曲线不会相交
虽然在同一等产量图中,有无数条等产量线,但都平行,不会相交,这是因为一旦相交,那么意味着两条线上所有的点的产量都与交点处相同,这会与特征(1)产生矛盾。
(3)等产量曲线斜率为负
等产量曲线向右下方倾斜,在技术不变的情况下,想要保持产量不变,减少一种要素的投入必须增加另一种要素的投入,因此劳动力和资本的投入量呈现反向关系。边际技术替代率的公式表明,边际技术替代率就是等产量曲线的斜率。由于ΔK和ΔL的符号相反,故边际技术替代率为负,等产量曲线的斜率为负,等产量曲线向右下方倾斜。
(4)等产量曲线凸向原点
由于边际技术替代率就是等产量曲线的斜率,而且边际技术替代率逐渐减少,故等产量曲线的斜率为负,且绝对值递减,凸向原点。
3.特殊形状的等产量线
若两种要素投入完全不能替代,只要其中一种要素投入固定不变,不论另一种要素投入怎样增加,产量始终不变。此时要增加产量,就必须按既定的比例同时增加两种要素投入,等产量曲线呈L状。
(二)等成本线
等成本线就是指在要素价格既定的条件下,厂商花费一定成本所能购买的两种要素最大数量组合的轨迹。如果用C表示既定的成本,w和r分别代表劳动L和资本K的价格,则等成本线的方程为:C=wL+rK,斜率为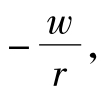 是两种要素的价格之比,是在既定的要素价格与成本约束下,厂商在市场上为增加一单位劳动的购买所必须减少的资本购买量。
是两种要素的价格之比,是在既定的要素价格与成本约束下,厂商在市场上为增加一单位劳动的购买所必须减少的资本购买量。

图4-6 等成本线
上图中的曲线C1即为等成本线,等成本线把坐标空间分成三部分:等成本线左下方区域、右上方区域和等成本线本身,等成本线上表明每一点购买的劳动力和资本所消费的全部成本都是C1,花掉了厂商的全部预算,这条线也就是厂商的预算边界;等成本线左下方区域表明成本没有完全花完,还有剩余或存在浪费;等成本线右上方区域表明预算超出,是现有成本不能达到的点。
在成本C、资本的价格r和劳动力的价格w都不变的情况下,等成本保持不动,但当其中的任意一方发生变化时,等成本线将会发生移动。
第一种情况:资本的价格r和劳动力的价格w不变,成本C发生变化,此时等成本线将会平行移动,成本增加,平行右移,成本减少,平行左移。如图4-7所示。

图4-7 等成本线的移动-1
第二种情况:成本C不变,资本的价格r和劳动力的价格w同比例同方向发生变化,此时等成本线也会发生平移,同比增加,等成本线左移;同比减少,等成本线右移。如图4-8所示。
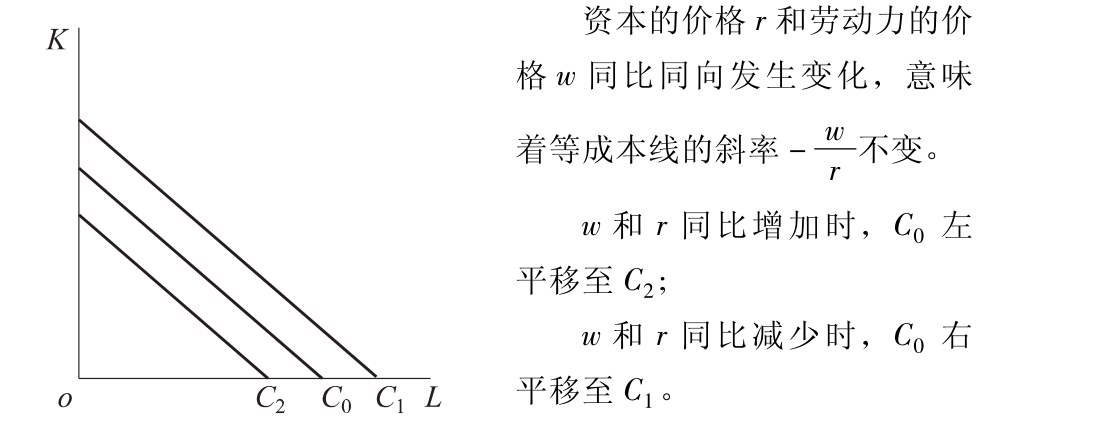
图4-8 等成本线的移动-2
第三种情况:成本C不变,两种要素价格一种保持不变,另一种价格提升或下降,此时等成本线将会以不变的一方与坐标轴交点为圆心,内外旋转,价格上升,向内转;价格下降,向外转。如图4-9所示。

图4-9 等成本线的移动-3
第四种情况:成本C、资本的价格r和劳动力的价格w都同比例同方向发生变化,此时等成本线不发生任何变化,这是因为无论斜率还是截距都不发生变化,即厂商的全部预算用来购买的两种要素数量不发生任何变化。
第五种情况:成本C、资本的价格r和劳动力的价格w不同比例不同方向发生变化,此时等成本线的斜率和截距都发生变化,等成本线发生不规则变化。
(三)生产要素的最优组合
L1由于在长期,各种要素的投入数量都是可以改变的,无论劳动力、生产工具还是厂房、设备,都可以根据产量进行调整,因此理性的厂商会选择最优的生产要素组合进行生产,达到成本既定时产量最大,或是产量既定时成本最小。
1.成本既定的产量最大化
假定企业用两种可变生产要素劳动和资本生产一种产品,劳动的价格w和资本的价格r是已知的,企业用于购买这两种要素的全部成本C是固定的。如果企业要从既定的成本中获得最大的产量,那么它应该如何选择最优的劳动投入量和资本投入量呢?
把企业的等产量曲线和相应等成本曲线画在同一个平面坐标系中,就可以得到企业在既定成本下实现最大产量的最优要素组合点,即生产的均衡点。如图4-10所示。

图4-10 成本既定的产量最大化
等成本线C1代表了一个既定的成本量,与其中的一条等产量曲线Q2相切于E点,该点就是生产的均衡点。它表示:在既定成本条件下,企业应该如何按照E点的要素组合进行生产,即劳动投入量和资本投入量分别为L1和K1,这样,厂商就会取得最大的产量。
尽管等产量曲线Q3代表的产量高于等产量曲线Q2,但唯一的等成本线C1与等产量曲线Q3无交点又无切点,表明线Q3所代表的产量是企业无法实现的,因为企业利用既定成本只能购买到位于等成本线C1上或等成本线C1以内区域的要素组合。再看等产量曲线Q1,虽然与唯一的等成本线相交于A、B两点,但等产量曲线Q1所代表的产量是比较低的。因为,此时企业在不断增加成本的情况下,只需由A点出发向右或由B点出发向左沿着既定的等成本线C1改变要素组合,就可以增加产量。所以,只有在唯一的等成本线C1和产量曲线Q2的相切点E,才是实现既定成本条件下的最大产量的要素组合,任何更高的产量在既定成本条件下都是无法实现的,任何更低的产量都是低效率的。
2.产量既定的成本最小化
若企业要求生产的产量既定,劳动的价格w和资本的价格r已知,如企业要投入最小的成本中获得该既定产量,那么它应如何选择最优的劳动投入量和资本投入量呢?
图4-11中有一条等产量曲线Q0和三条等成本曲线C0、C1和C2,唯一的等产量曲线Q0代表既定的产量。三条等成本线具有不同的成本量,其中等成本线C1代表的成本大于等成本线C0,等成本线C0代表的成本大于等成本线C2。唯一的等产量曲线Q0与其中一条等成本线C0相切于E点,这就是生产的均衡点或最优要素组合点。E点表示在既定的产量条件下,生产者应该选择E点的要素组合——投入K0数量的资本和L0数量的劳动,才能实现最小的成本。
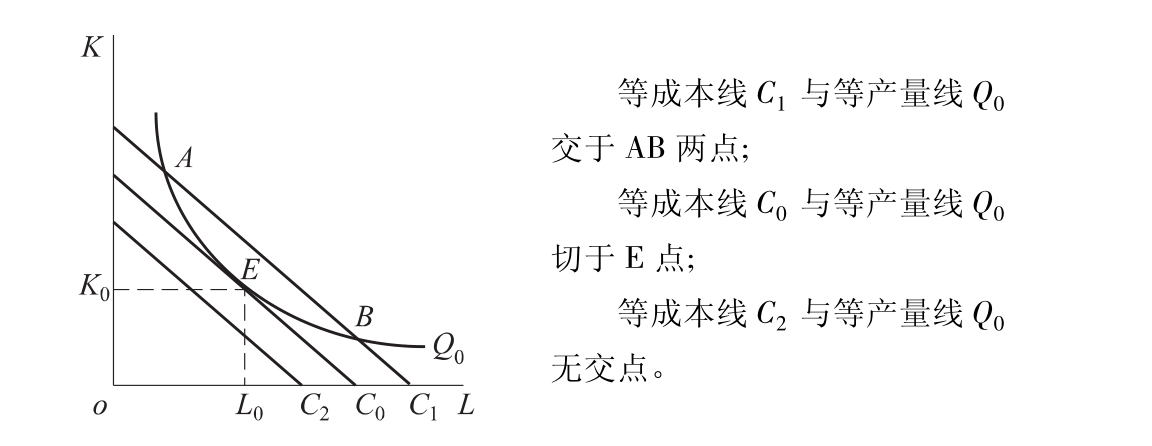
图4-11 产量既定的成本最小化
从图4-11可见,等成本线C2虽然代表的成本较低,但它与既定的等产量曲线Q0既无交点又无切点,它无法实现等产量曲线Q0所代表的产量。等成本曲线C1虽然与既定的等产量曲线Q0相交于A、B两点,但它所代表的成本过高,通过沿着等产量曲线Q0由A点向E点或者由B点向E点的移动,就可以获得相同的产量而使成本下降。所以,只有在切点E,才是在既定产量条件下实现最小成本的要素组合。
3.要素投入的最优选择
根据以上两个部分的分析,我们可以得出结论:等产量曲线和等成本曲线的切点所代表的组合就是要素投入的最优组合。如图4-12所示。

图4-12 要素投入的最优选择
由于等产量线的斜率为MRTSLK=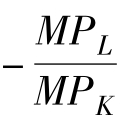 ,等成本线的斜率为
,等成本线的斜率为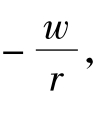 当两者在E点相切时,等产量线的斜率与等成本线的斜率相等,因此会出现:
当两者在E点相切时,等产量线的斜率与等成本线的斜率相等,因此会出现: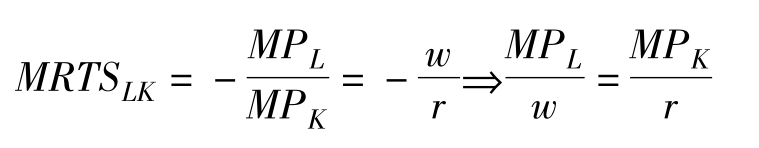
也就是说厂商为了选择最优要素组合,必须按一定比例购买两种要素,使得花费在两种要素上的最后一单位成本所带来的边际产量相等,这样也能够实现厂商的利润最大化,这就是长期生产函数中生产者均衡的条件。
4.生产扩展线
在技术水平、生产要素价格和其他条件都不变的情况下,如果企业改变成本,等成本线会发生平移;如果企业改变产量,等产量线会发生平移。这些不同的等产量线和等成本线相切,会形成一系列不同的生产均衡点,这些均衡点的轨迹就是拓展线。如图4-13所示。
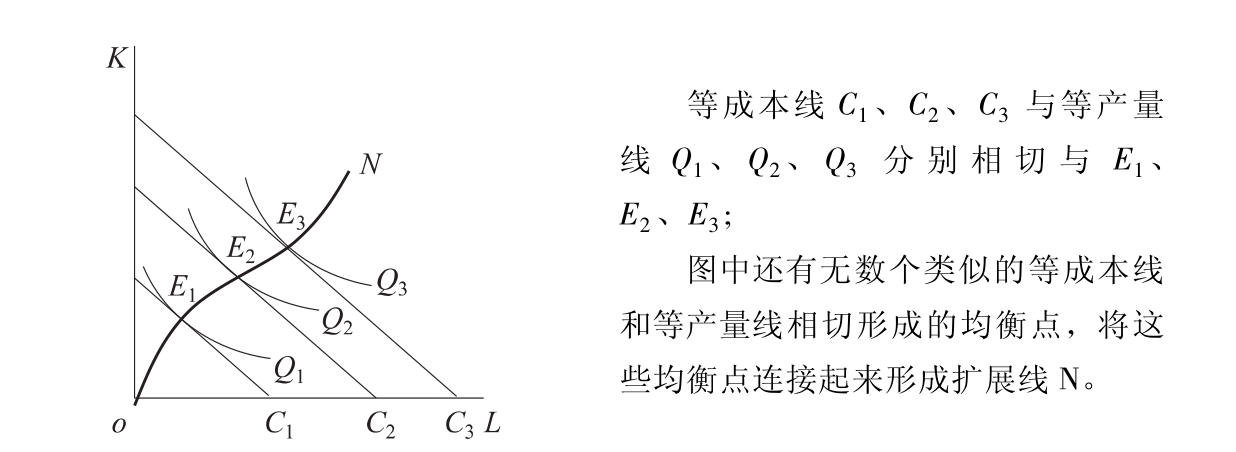
图4-13 扩展线
在生产要素价格、生产技术和其他条件不变的情况下,当生产规模发生变化时,为了追求利润最大化,厂商必然会沿着扩展线来进行要素投入的组合,从而实现成本既定的产量最大化和产量既定的成本最小化。拓展线是厂商在长期扩张和收缩生产时所必须遵循的路线。
若扩展线是射线,表明劳动和资本的比例不变;如果下凹,表明劳动的比重增加,生产扩展走的是劳动密集型的道路;如果上凹,表明资本的比重增加,生产扩展走的是资本密集型的道路。
5.脊线和生产的经济区域
等产量曲线上斜率为零的点或斜率为无穷大的点与原点的连线叫脊线。
在脊线OB左上方和OA右下方,等产量曲线的斜率为正,意味着为了维持某一产量水平,劳动和资本必须同时增加。因此,其中一种要素的边际产量必然小于零:在脊线OB上方,MPK<0,此时,在劳动投入不变的条件下,减少资本投入反而增加产量;脊线OA下方,MPL<0,此时,在资本投入不变的条件下,减少劳动投入反而增加产量。因此,脊线OB代表生产各种产量所使用的资本量的最高限,脊线OA代表生产各种产量所使用的劳动量的最高限。显然,理性的厂商总是在两条脊线所围的区域内从事生产。如图4-14所示。
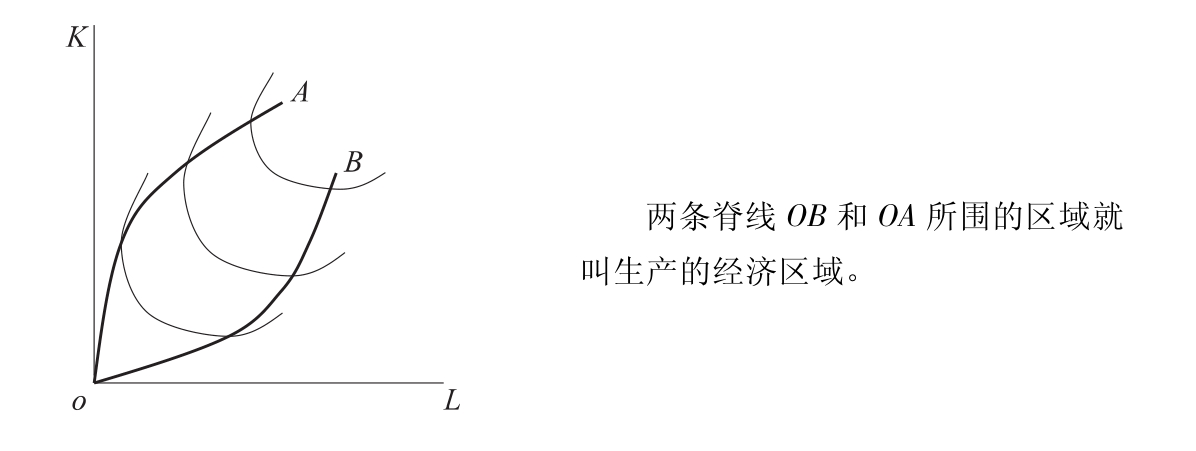
图4-14 脊线和生产的经济区域
四、规模报酬
规模报酬变动是指所有要素投入同时、同方向和同幅度变动时引起的产量变动,根据产业类型和企业所处阶段的不同可以分为规模报酬递增、规模报酬不变和规模报酬递减三个阶段。
(一)规模报酬不变
在这个阶段,产量的变动幅度等于各种要素的变动幅度。生产函数若为Q=f(L,K),当劳动力和资本的投入量都扩大λ倍时,生产规模同比扩张,产量扩大λ倍,表现为λQ=f(λL,λK)。如图4-15所示。

图4-15 规模报酬不变
(二)规模报酬递增
在这一阶段,产量的变动幅度大于各种要素的变动幅度,若生产函数为Q=f(L,K),当劳动力和资本的投入量都扩大λ倍时,生产规模的扩张带来了效率的提高,产量扩大的倍数大于λ倍,表现为λQ<f(λL,λK),如图4-16所示,这是由于:
(1)分工协作带来的专业化利益。生产规模扩大时,使用的劳动较多,劳动者可以进行专业化分工,从而提高效率。专业化利益有时也体现在资本设备上。例如当厂商扩大规模时,可以用效率更高的专门化的资本设备来代替非专门化的设备。
(2)某些要素的不可分割性。有些要素如电子计算机、自动化装配线等必须在生产规模达到足够大的程度时才能有效率地使用。当规模很小时,使用这些不可分割的设备,是得不偿失的。

图4-16 规模报酬递增
(三)规模报酬递减
在这个阶段,产量的变动幅度小于各种要素的变动幅度。若生产函数为Q=f(L,K),当劳动力和资本的投入量都扩大λ倍时,生产规模的扩张带来了效率的降低,产量扩大的倍数小于λ倍,表现为λQ>f(λL,λK),如图4-17所示,这是由于:

图4-17 规模报酬递减
当厂商不断地扩大经营规模时,上述导致规模报酬递增的有些因素的作用最终会受到限制,并走向它的反面,导致规模报酬递减。
企业规模报酬递减的主要原因,是由于规模过大遇到的管理方面的困难。当企业规模变得越来越大时,管理和协调的问题也就日益难以处理:管理层次的增加,使得信息在传递过程中容易失真。每一个企业只能有一个首席执行官、一个财务主管和一个董事会。由于只能用更少的时间研究每一个市场和制定每一个决策,高层管理人员可能变得脱离日常生产活动,并且开始犯错误。因此,尽管技术、专业化等可以提供递增或不变的规模报酬,但管理和控制方面的问题会在那些巨大的企业中导致规模报酬递减。
生活中的经济学
适合的生产规模
台塑集团的老板王永庆被称为“主宰台湾的第一个企业家”、“华人经营之神”,他的事业从台塑生产塑胶粉粒PVC开始,当时每月仅生产100吨PVC,在世界上规模最小。王永庆知道要降低PVC的成本只有扩大产量,降低成本。于是,他冒着产品积压的风险,把产量扩大到1 200吨/月,并以低价格迅速占领世界市场。
香港有家父子俩经营的皮鞋作坊,厂店合一,手工定做。他们根据每个人的脚型制作,穿着极为舒适,价格和名气远超一些世界名牌。李嘉诚、金庸等名人均穿他们的鞋。这样的鞋厂在世界上还有不少,如制鞋大国意大利,60%的名牌鞋都出自小厂,80%的厂家在20人以下。
可见企业并非一味求大或求小,要根据行业特点追求最大效益,盲目合并企业的做法往往事与愿违,绑在一起的小舢板绝非航空母舰。王永庆的成功不在于台塑大,而在于台塑实现了规模收益递增的最优规模。
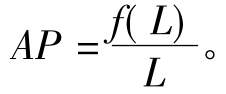

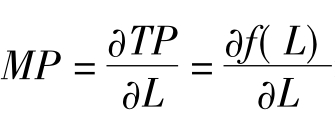 看,边际产量就是总产量曲线的斜率。由于总产量曲线先上凹后下凹,故在总产量曲线的拐点A,斜率极大,即边际产量极大。在此以前,斜率递增,即边际产量递增。此点以后,斜率递减,即边际产量递减。
看,边际产量就是总产量曲线的斜率。由于总产量曲线先上凹后下凹,故在总产量曲线的拐点A,斜率极大,即边际产量极大。在此以前,斜率递增,即边际产量递增。此点以后,斜率递减,即边际产量递减。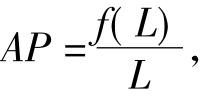 所以平均产量就是从原点向总产量曲线所作射线的斜率。由于总产量曲线先上凹后下凹,故从原点向总产量曲线所作的射线正好切于总产量曲线时,射线的斜率极大,即平均产量极大。在切点C以前,射线的斜率递增,即平均产量递增。在切点C以后,射线的斜率递减,即平均产量递减。
所以平均产量就是从原点向总产量曲线所作射线的斜率。由于总产量曲线先上凹后下凹,故从原点向总产量曲线所作的射线正好切于总产量曲线时,射线的斜率极大,即平均产量极大。在切点C以前,射线的斜率递增,即平均产量递增。在切点C以后,射线的斜率递减,即平均产量递减。

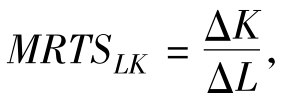 也可以表示为
也可以表示为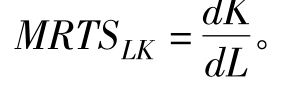 由于边际报酬递减,当厂商不断地用劳动替代资本时,随着劳动投入的增加,劳动的边际产量日益减少;随着资本投入的减少,资本的边际产量日益增加。因此,边际技术替代率具有递减的趋势。如图4-5所示。
由于边际报酬递减,当厂商不断地用劳动替代资本时,随着劳动投入的增加,劳动的边际产量日益减少;随着资本投入的减少,资本的边际产量日益增加。因此,边际技术替代率具有递减的趋势。如图4-5所示。
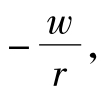 是两种要素的价格之比,是在既定的要素价格与成本约束下,厂商在市场上为增加一单位劳动的购买所必须减少的资本购买量。
是两种要素的价格之比,是在既定的要素价格与成本约束下,厂商在市场上为增加一单位劳动的购买所必须减少的资本购买量。






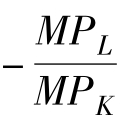 ,等成本线的斜率为
,等成本线的斜率为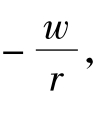 当两者在E点相切时,等产量线的斜率与等成本线的斜率相等,因此会出现:
当两者在E点相切时,等产量线的斜率与等成本线的斜率相等,因此会出现: