-
1.1前 言
-
1.2模块一 机械制图的基本知识
-
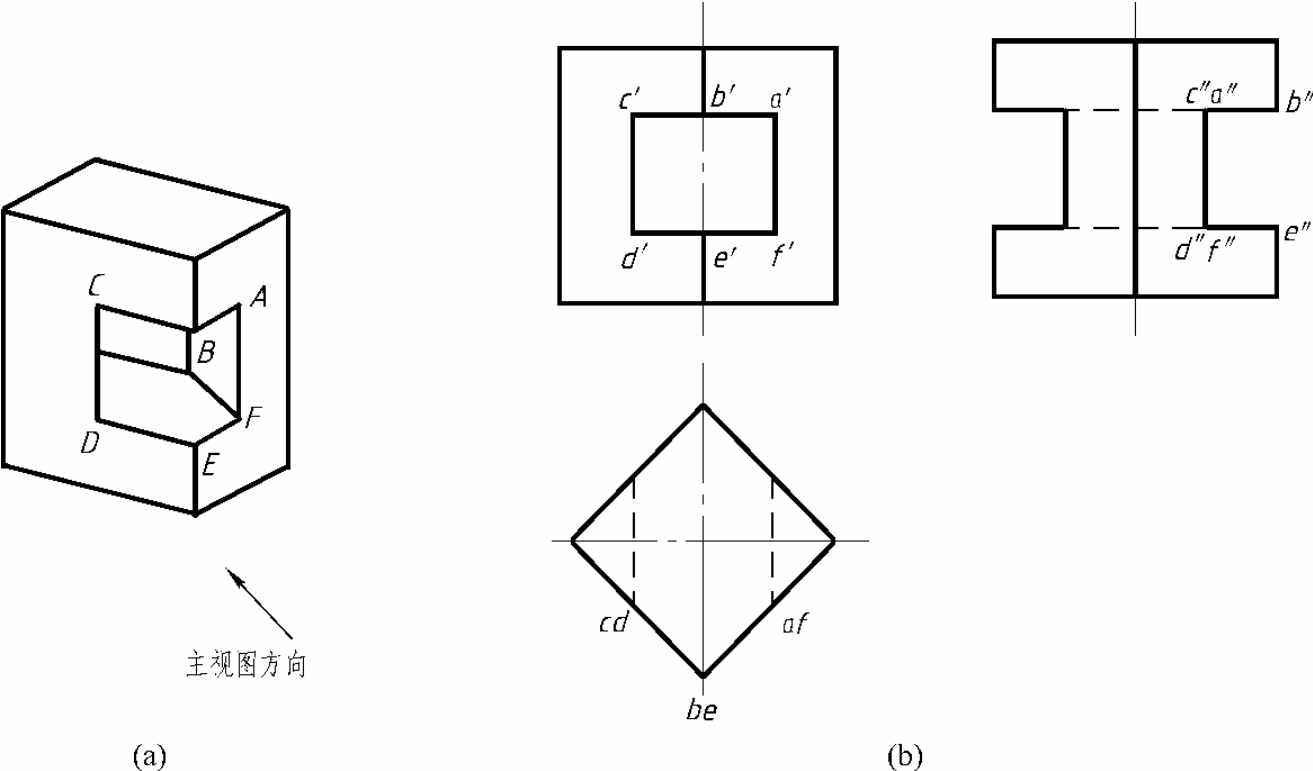
1.2.11.1 表达立体的几种图
-
1.2.21.2 三视图的形成及其相互关系
-
1.2.31.3 正投影的基本性质
-
1.3模块二 绘图工具和绘图的基本技能
-
1.3.12.1 绘图工具及其使用
-
1.3.22.2 国家标准《机械制图》的基本规定
-
1.3.32.3 平面几何图形的画法
-
1.3.42.4 斜度和锥度
-
1.3.52.5 线段连接的画法
-
1.4模块三 点、线、面的投影
-
1.4.13.1 点的投影
-
1.4.23.2 各种位置直线的投影
-
1.4.33.3 各种位置平面的投影
-
1.5模块四 基本体的投影
-
1.5.14.1 平面基本体的投影
-
1.5.24.2 曲面基本体的投影
-
1.5.34.3 基本体的尺寸标注
-
1.6模块五 组 合 体
-
1.6.15.1 叠加式组合体的画图
-
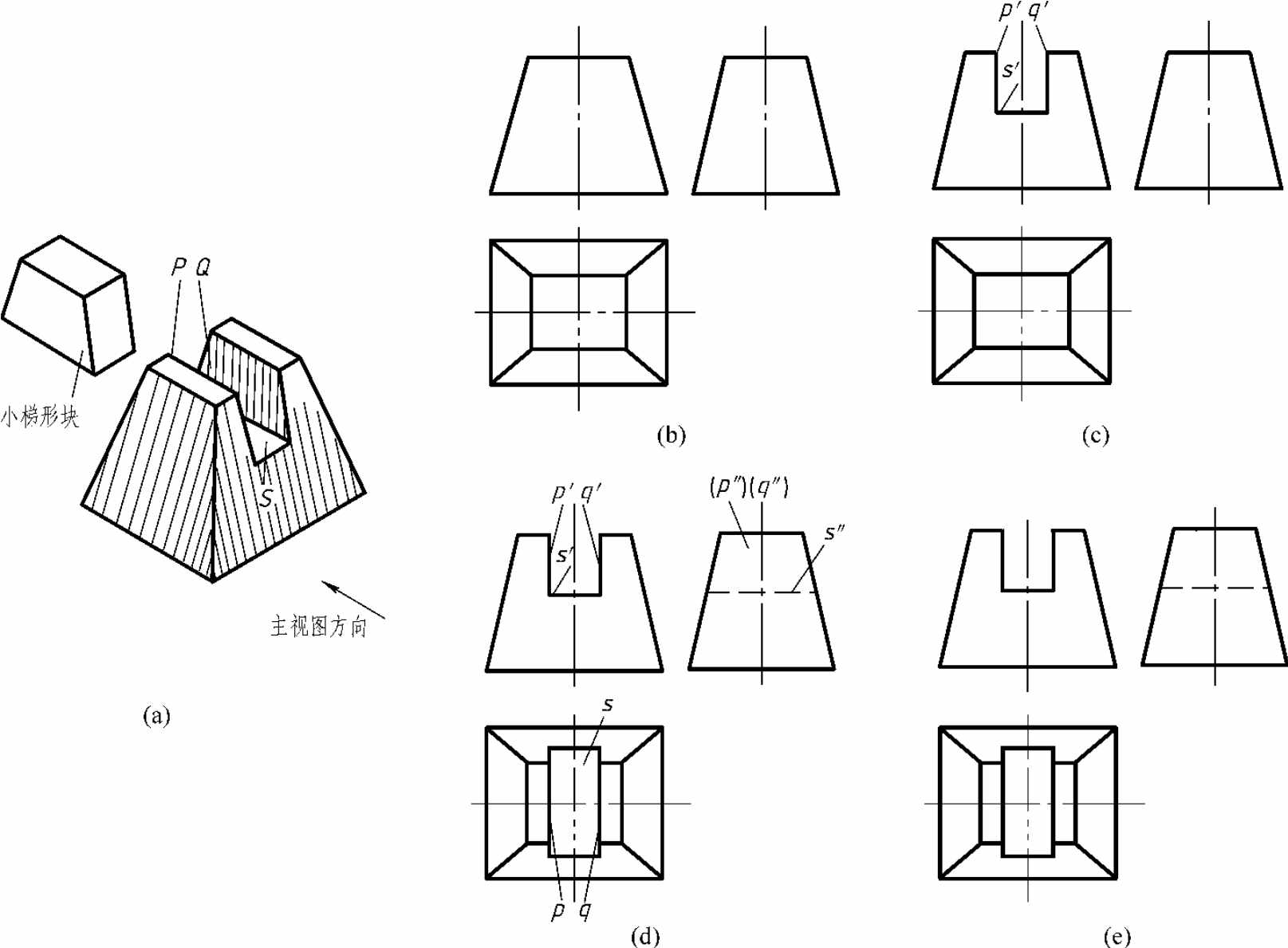
1.6.25.2 切割式组合体的画图
-
1.6.35.3 组合体的尺寸标注
-
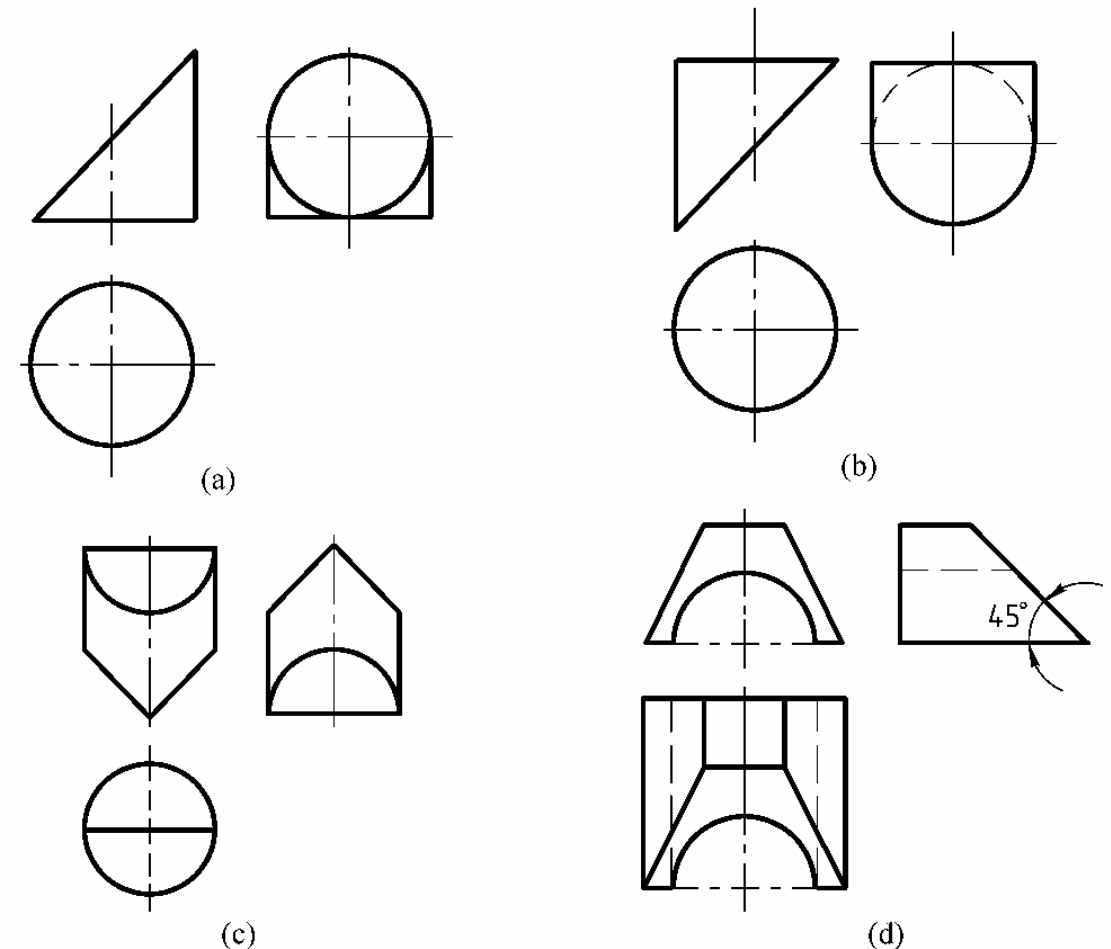
1.6.45.4 叠加式组合体的读图
-
1.6.55.5 切割式组合体的读图
-
1.7模块六 截交线和相贯线
-
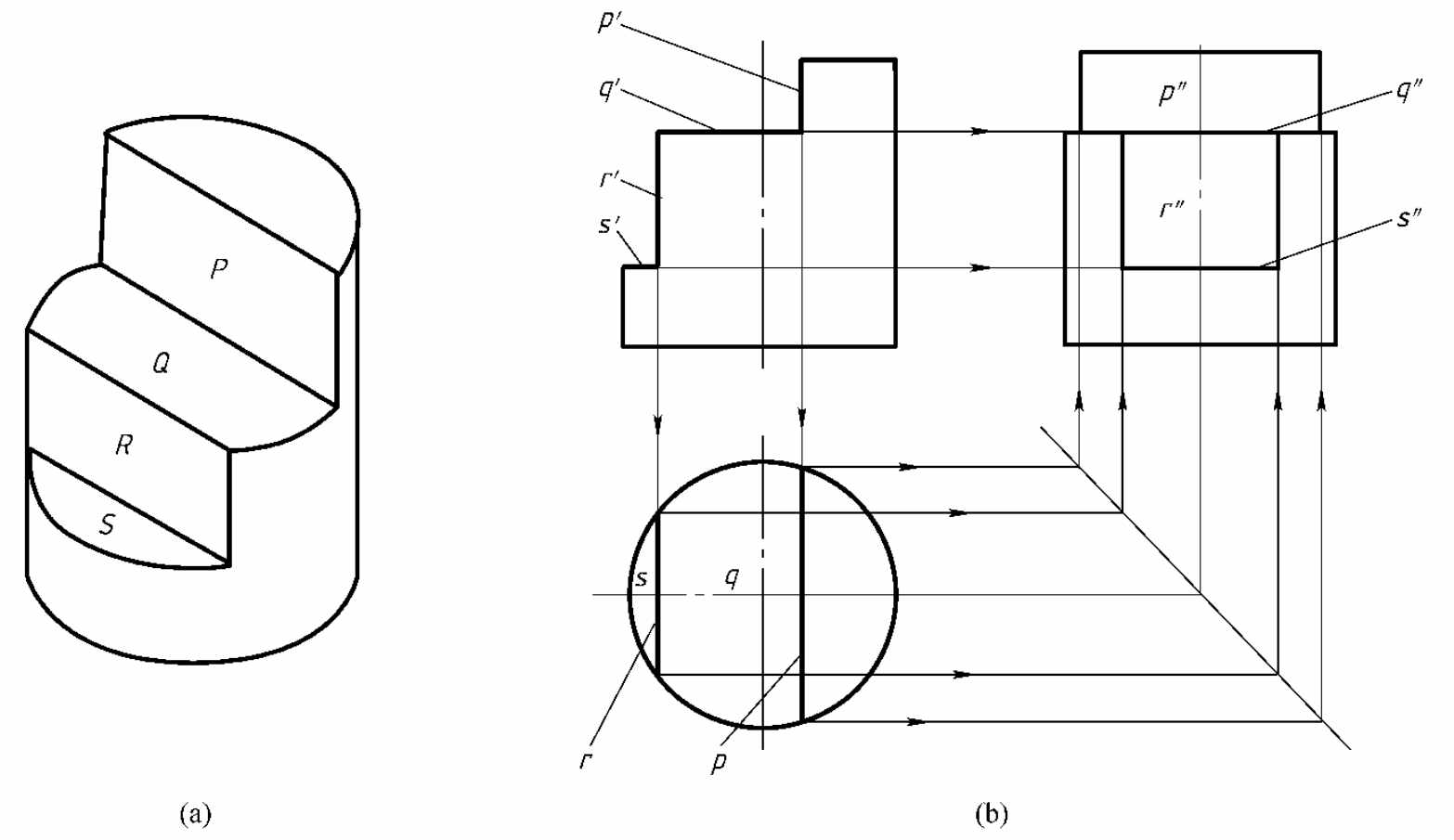
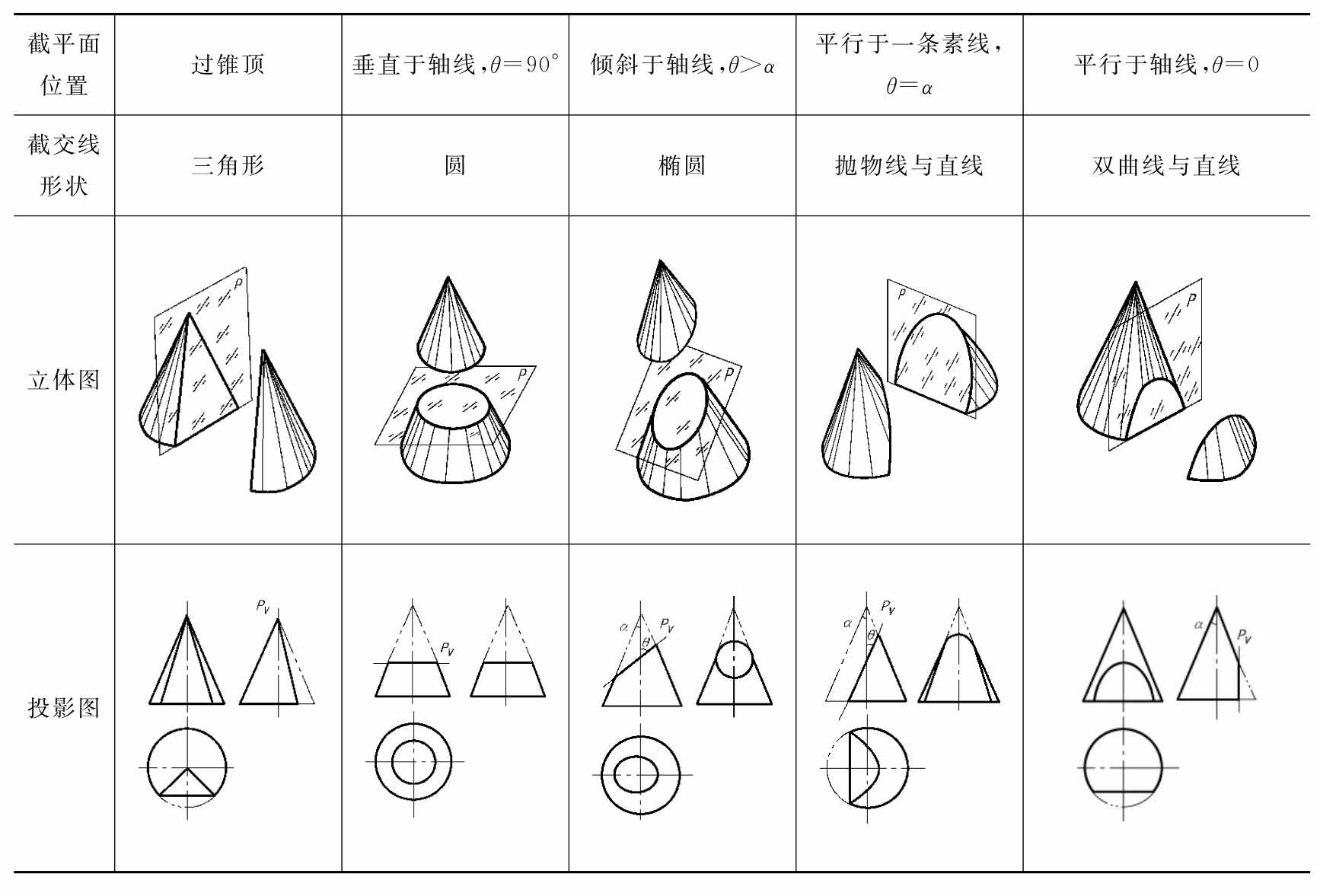
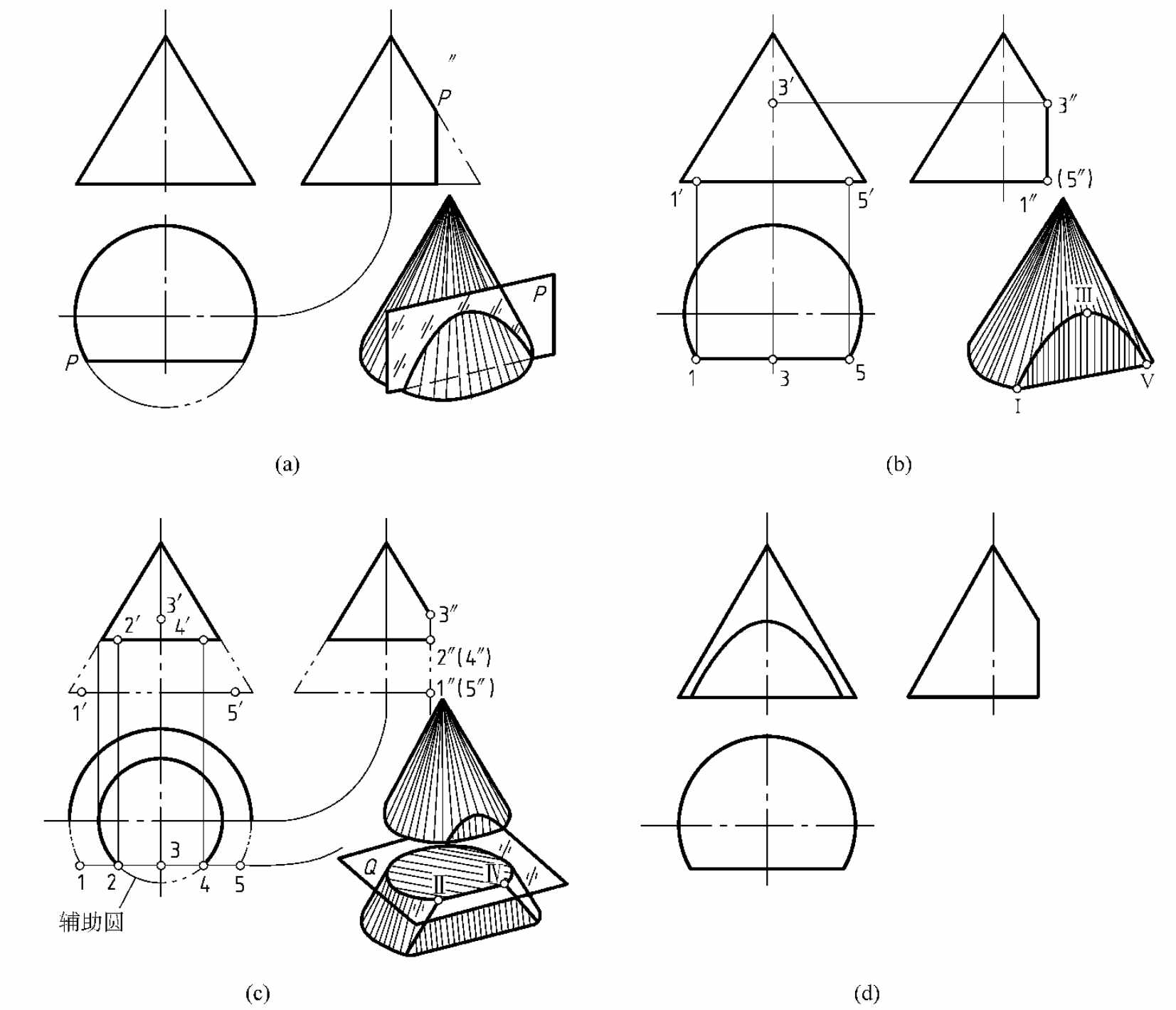
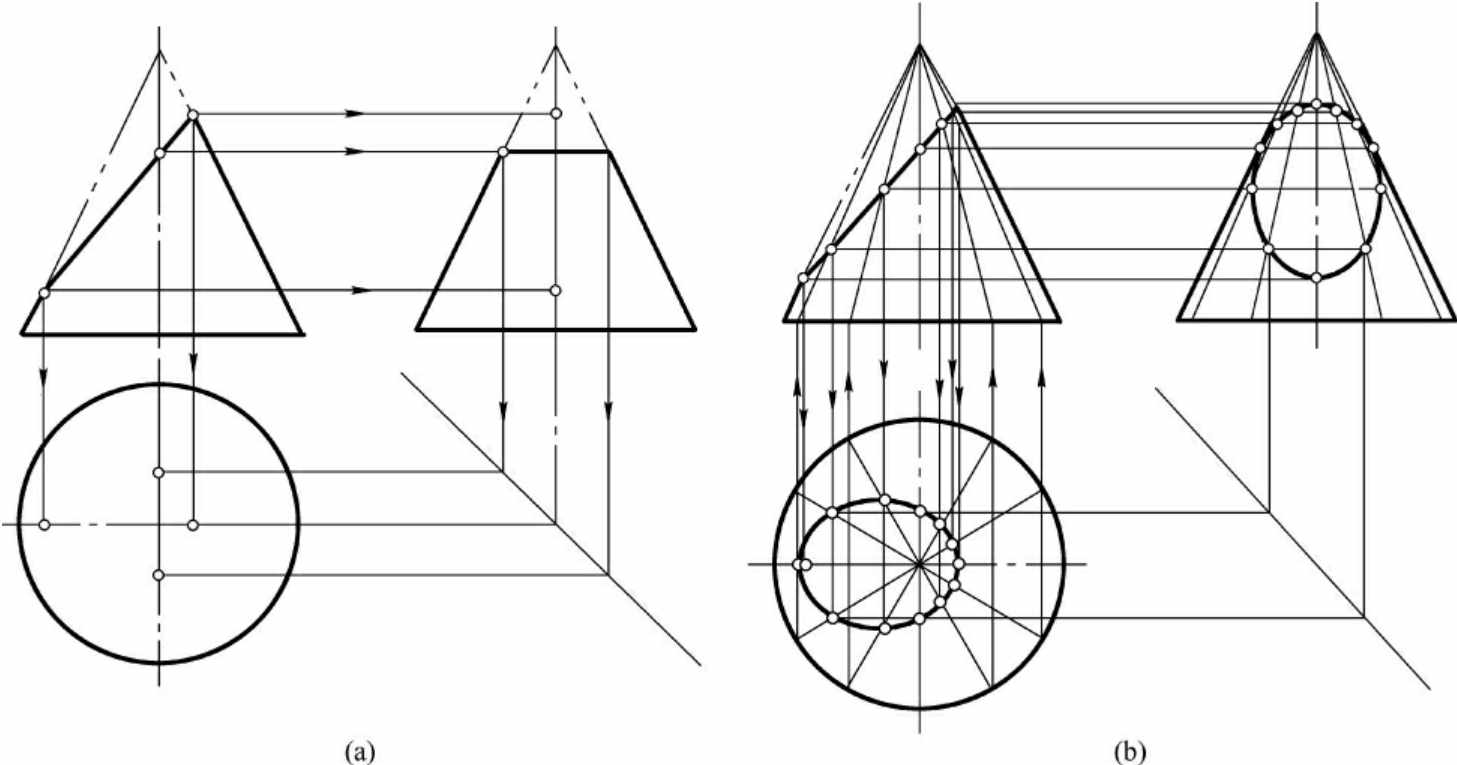
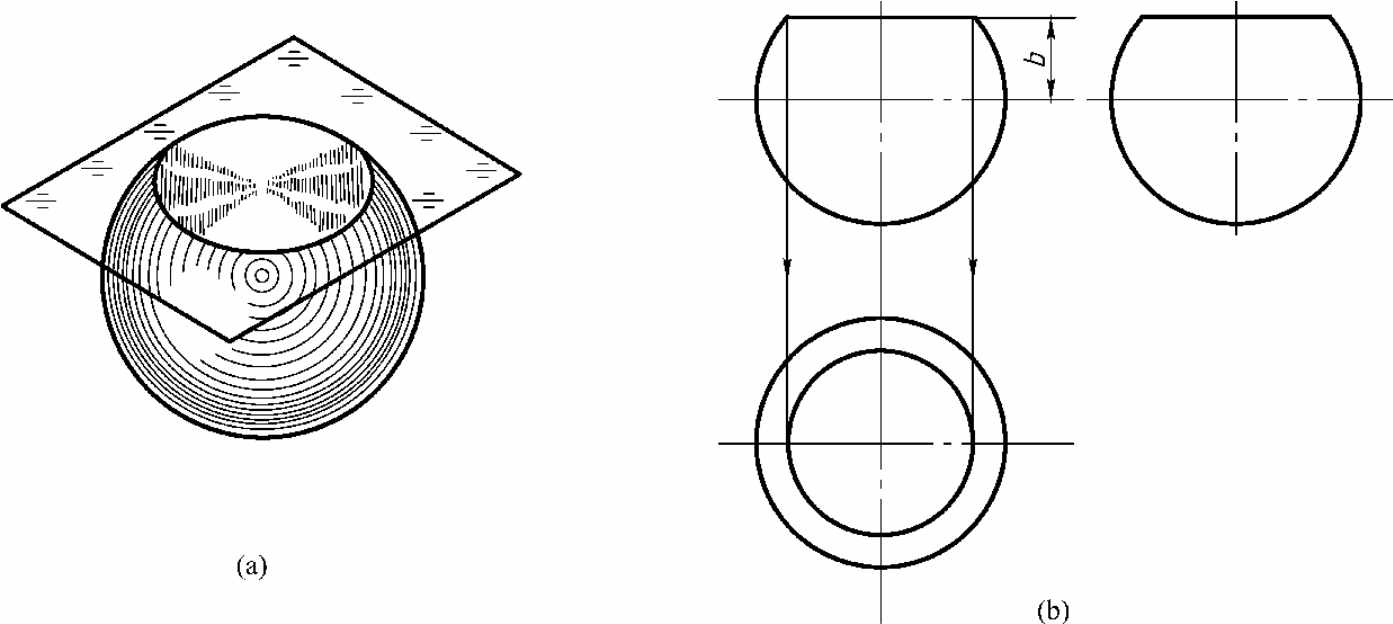
1.7.16.1 截交线
-
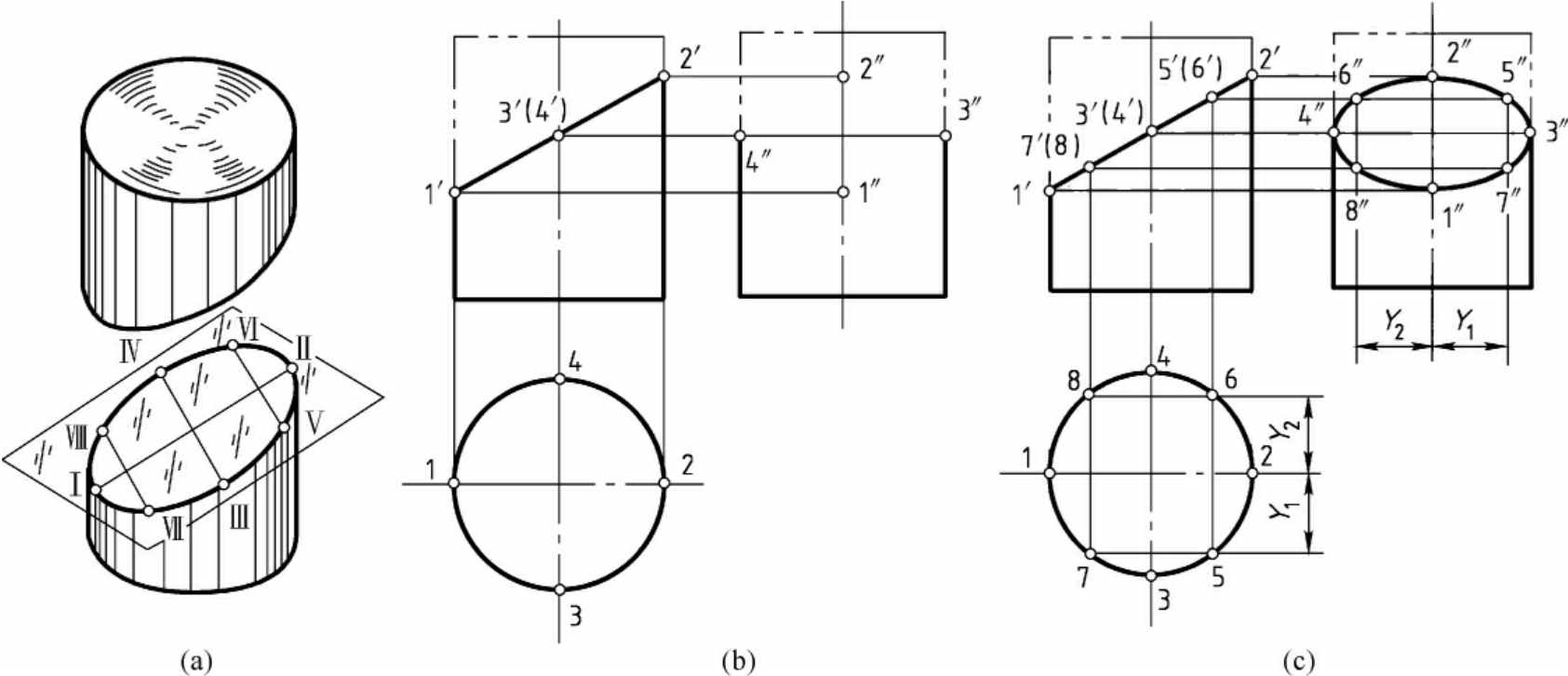
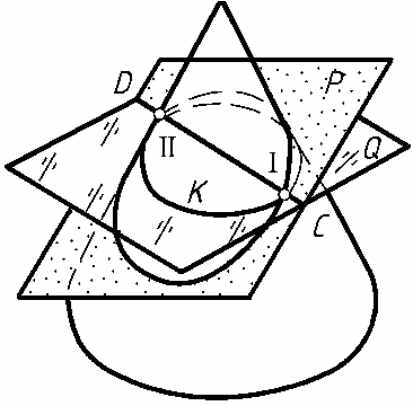
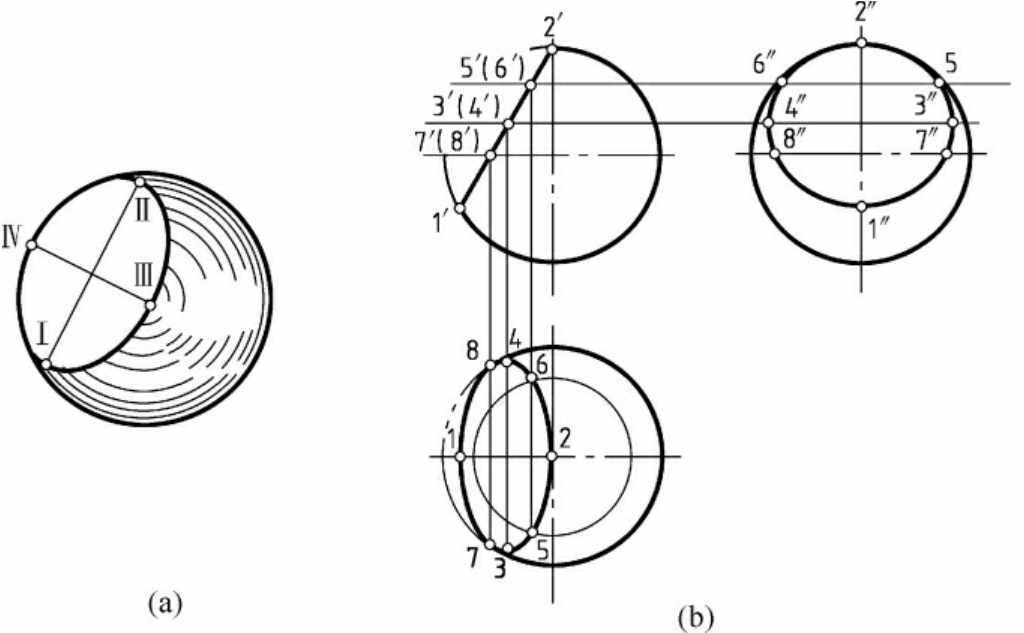
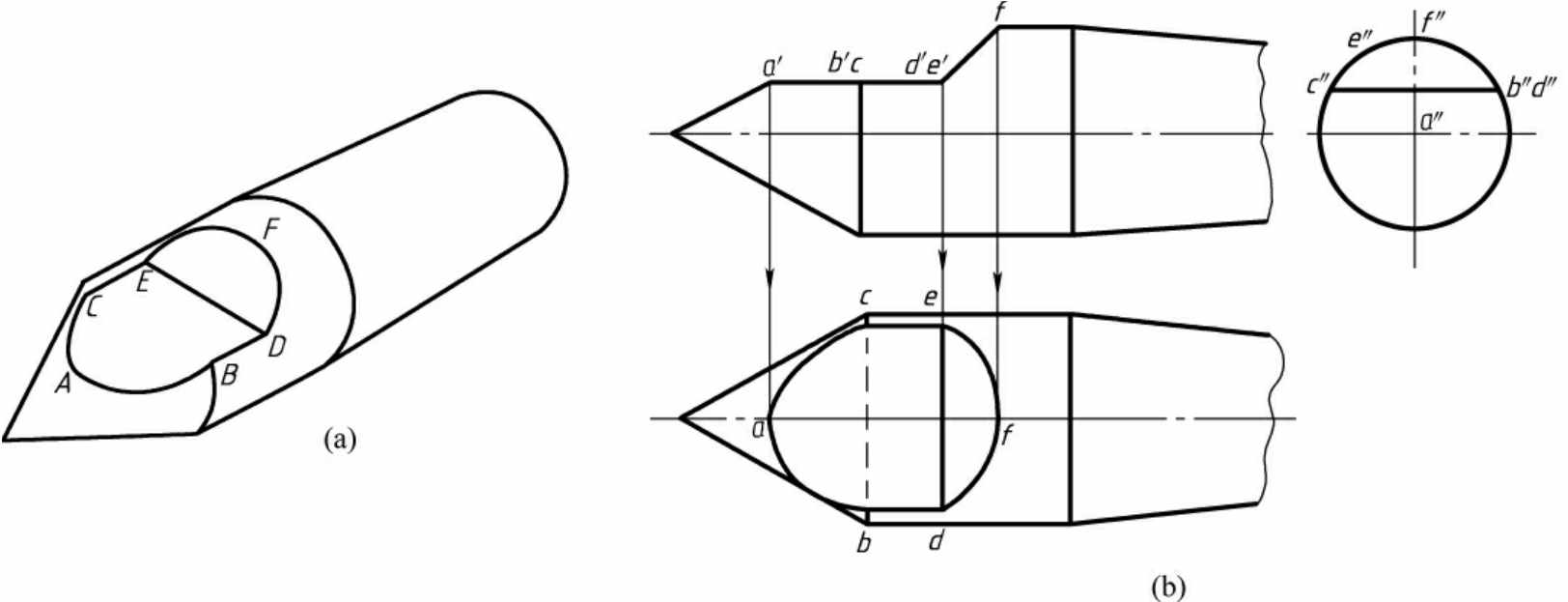
1.7.26.2 相贯线
-
1.8模块七 轴 测 图
-
1.8.17.1 轴测图的基本知识
-
1.8.27.2 正等测图
-
1.8.37.3 斜二测图
-
1.8.47.4 轴测剖视图
-
1.8.57.5 轴测草图
-
1.9模块八 零 件 图
-
1.9.18.1 零件图的概念和分类
-
1.9.28.2 零件图的画图和读图
-
1.10模块九 装 配 图
-
1.10.19.1 装配图的作用、内容及画法概述
-
1.10.29.2 画装配图
-
1.10.39.3 读装配图
-
1.10.49.4 第三角投影体系的装配图举例
-
1.11模块十 薄板类零件图的识读和展开
-
1.11.110.1 平面立体零件图的识读和展开
-
1.11.210.2 曲面立体零件图的识读和展开
-
1.11.310.3 变形接头零件图的识读与展开
-
1.11.410.4 生产中画展开图要考虑的工艺因素
-
1.12附 录
-
1.13参考文献
1
机械制图