-
1.1《甘肃省耕地质量评价系列丛书》编委会
-
1.2《瓜州县耕地质量评价》编写组
-
1.3序言
-
1.4前言
-
1.5目录
-
1.6第一章 自然与农业生产概况
-
1.6.1第一节 地理位置与行政区划
-
1.6.1.1一、地理位置
-
1.6.1.2二、行政区划
-
1.6.1.3三、发展布局
-
1.6.2第二节 自然与社会经济概况
-
1.6.2.1一、气候资源概况
-
1.6.2.2二、水资源概况
-
1.6.2.3三、植被
-
1.6.2.4四、农业生产概况
-
1.6.3第三节 耕地立地条件及农田基础设施
-
1.6.3.1一、耕地立地条件状况
-
1.6.3.2二、耕地土壤类型及土壤面积类型
-
1.6.3.3三、农田基础设施状况
-
1.6.4第四节 耕地改良利用与生产状况
-
1.6.4.1一、农业生产施肥概况
-
1.6.4.2二、设施农业建设
-
1.6.4.3三、当地主要的耕地改良模式及效果
-
1.6.4.4四、耕地利用程度与耕作制度
-
1.6.5第五节 耕地利用改良与保护的简要回顾
-
1.6.5.1一、第二次土壤普查对耕地质量建设取得的成就
-
1.6.5.2二、改革开放以来实施的农业重点项目
-
1.6.5.3三、生态环境建设
-
1.6.5.4四、商品粮棉基地和蜜瓜储运保鲜基地建设
-
1.6.5.5五、农业综合开发
-
1.6.5.6六、加强耕地保养管理的政策法规与措施
-
1.7第二章 野外调查与土样采集与分析
-
1.7.1第一节 基本情况与土壤理化性状调查
-
1.7.1.1一、基本情况调查
-
1.7.1.2二、土壤理化性状调查
-
1.7.2第二节 调查方法步骤与样品采集
-
1.7.2.1一、布点的原则和方法
-
1.7.2.2二、样品采集
-
1.7.3第三节 样品制备、分析与测试质量控制
-
1.7.3.1一、样品制备
-
1.7.3.2二、质量控制方法
-
1.8第三章 耕地土壤属性
-
1.8.1第一节 耕地土壤化学性状
-
1.8.1.1一、土壤pH值
-
1.8.1.2二、土壤有机质
-
1.8.1.3三、土壤氮素状况
-
1.8.1.4四、土壤磷含量状况
-
1.8.1.5五、土壤钾含量状况
-
1.8.1.6六、土壤微量元素含量状况
-
1.8.1.7七、土壤全盐
-
1.8.2第二节 耕地土壤物理性状
-
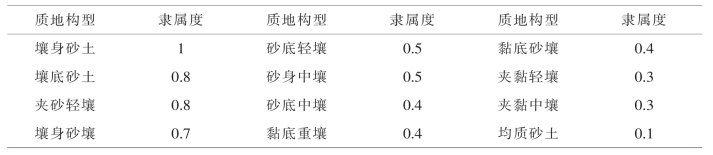
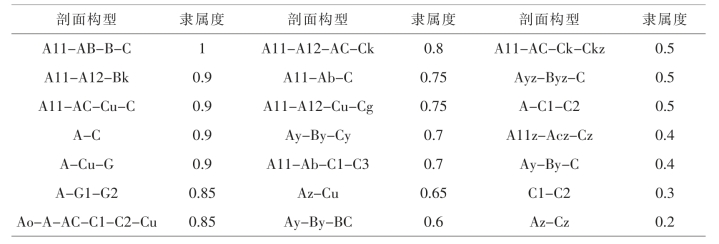
1.8.2.1一、土壤质地
-
1.8.2.2二、土壤容重
-
1.8.2.3三、土壤孔隙度
-
1.9第四章 耕地地力评价
-
1.9.1第一节 耕地地力评价基础工作
-
1.9.1.1一、耕地地力评价原理
-
1.9.1.2二、技术路线
-
1.9.2第二节 耕地地力评价
-
1.9.2.1一、建立县域耕地资源管理信息系统
-
1.9.2.2二、评价单元确定
-
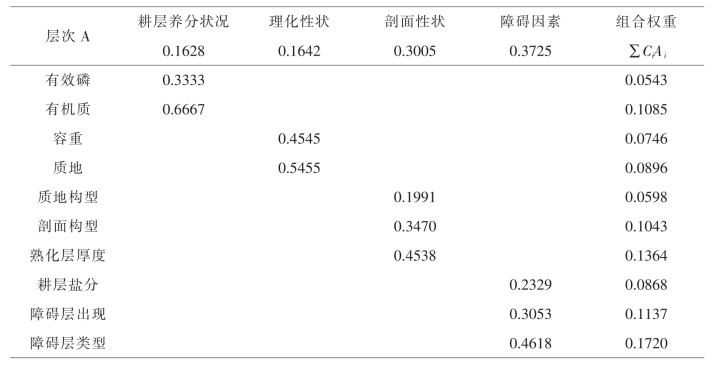
1.9.2.3三、评价指标选取
-
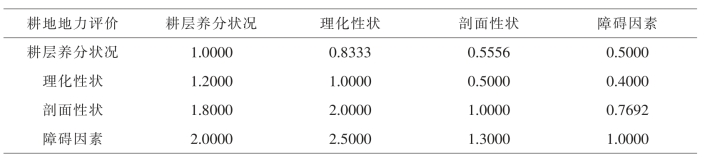
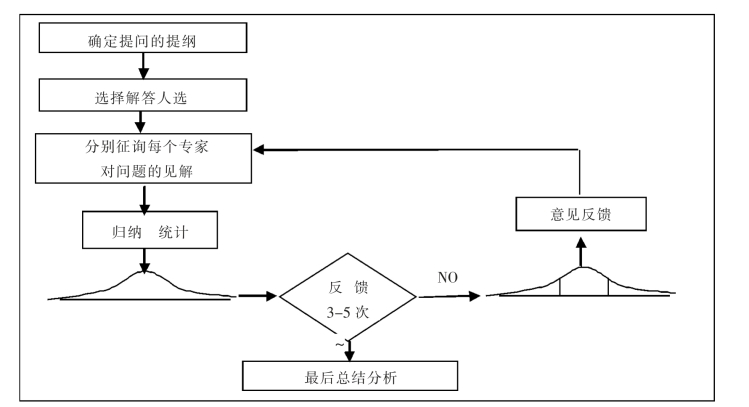
1.9.2.4三、单因素权重的确定(层次分析法)
-
1.9.2.5四、耕地地力等级的确定
-
1.10第五章 耕地地力评价结果与分析
-
1.10.1一、不同等级耕地面积统计与空间分布特征
-
1.10.1.1(一)不同等级耕地面积统计
-
1.10.1.2(二)不同等级耕地空间分布特征
-
1.10.2二、耕地地力等级分述
-
1.10.2.1(一)一等地
-
1.10.2.2(二)二等地
-
1.10.2.3(三)三等地
-
1.10.2.4(四)四等地
-
1.10.2.5(五)五等地
-
1.11第六章 瓜州县中低产土壤类型与改良利用分区研究
-
1.11.1一、目的意义
-
1.11.2二、土地利用现状
-
1.11.2.1(一)土地利用概况
-
1.11.2.2(二)土地利用现状
-
1.11.3三、中低产土壤类型及特点
-
1.11.3.1(一)沙化耕地型
-
1.11.3.2(二)瘠薄培肥型
-
1.11.3.3(三)障碍层次型
-
1.11.3.4(四)盐碱耕地型
-
1.11.4四、土壤改良利用分区系统及命名
-
1.11.5五、土壤改良利用分区概述
-
1.11.5.1(一)西部干三角洲农经高产培肥区
-
1.11.5.2(二)东部扇沿农林综合利用区
-
1.11.5.3(三)东南部泉水灌溉农牧合理利用区
-
1.11.5.4(四)南部盆地低产土壤改良区
-
1.11.5.5(五)绿洲外围滩利用区
-
1.11.6六、土壤改良利用措施
-
1.11.6.1(一)采取综合技术措施改良盐碱地
-
1.11.6.2(二)增施有机肥和种植绿肥
-
1.11.6.3(三)植树造林
-
1.12第七章 瓜州县蜜瓜产业发展潜力研究与对策
-
1.12.1一、目的意义
-
1.12.2二、基本情况
-
1.12.2.1(一)位置及区域特性
-
1.12.2.2(二)种植结构
-
1.12.2.3(三)土壤类型
-
1.12.2.4(四)土壤养分
-
1.12.2.5(五)适宜区的确定
-
1.12.3三、立地条件分析
-
1.12.3.1(一)土壤类型
-
1.12.3.2(二)海拔
-
1.12.4四、存在问题
-
1.12.4.1(一)种子市场管理不规范
-
1.12.4.2(二)知名品牌、区域品牌不多,主导产品市场占有率不高
-
1.12.4.3(三)技术力量薄弱,产业发展得不到保障
-
1.12.4.4(四)病虫害发生严重,制约着我县蜜瓜产业的发展
-
1.12.4.5(五)田间管理不规范,措施不到位
-
1.12.4.6(六)专业合作社职能得不到发挥,运作不规范
-
1.12.5五、瓜州蜜瓜产业发展的建议对策
-
1.12.5.1(一)加强农资市场管理,净化种子销售市场
-
1.12.5.2(二)优化布局,稳定蜜瓜产业规模,集约化生产
-
1.12.5.3(三)提高蜜瓜产品科技含量,创国内外市场知名品牌
-
1.12.5.4(四)加快发展蜜瓜加工龙头企业,推进蜜瓜产业化
-
1.12.5.5(五)完善检测、检疫设施,全面推行蜜瓜无公害标准化生产
-
1.12.5.6(六)加快蜜瓜批发市场建设,促进产品流通
-
1.12.5.7(七)积极发展中介组织,加快蜜瓜产业规模化发展
-
1.12.5.8(八)加强信息体系建设,为产业发展提供有力支持
-
1.12.5.9(九)建立有效的投入机制,为发展产业提供强有力的资金支持
-
1.12.5.10(十)加强试验示范的技术研究
-
1.13附表
1
瓜州县耕地质量评价